圆上点P到两点AB距离的和最大最小值

yuange1975

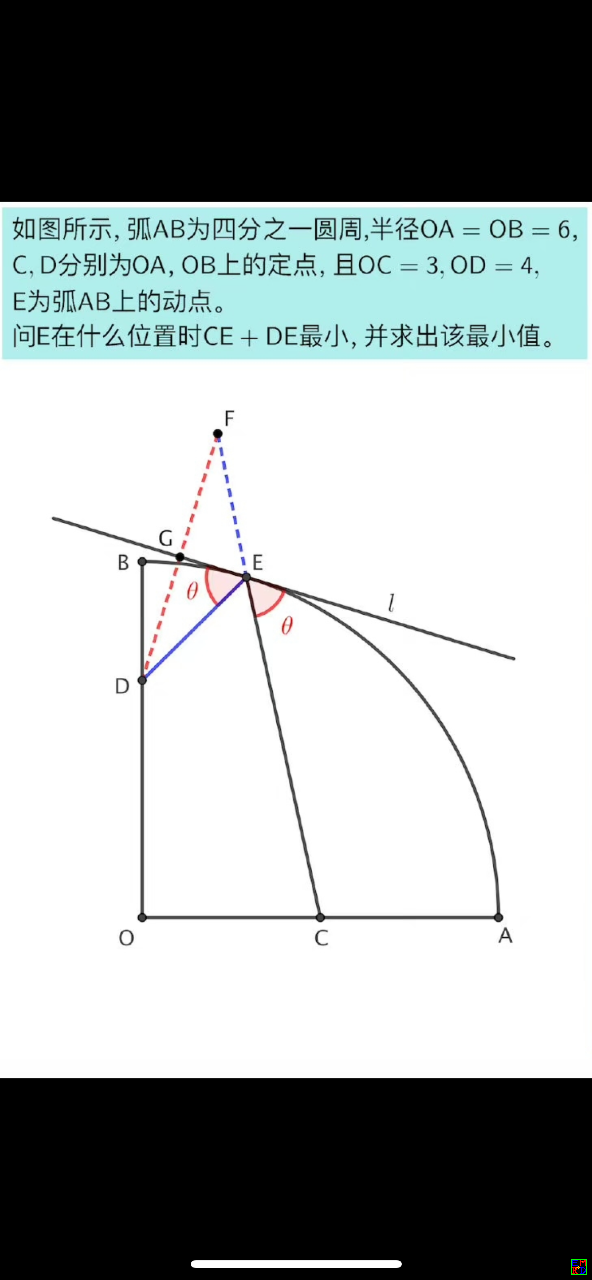
圆上点P到两点AB距离的和最大最小值。

AB两点坐标(-a,0)、(a,0)，a>=0。PA+PB=2m，椭圆方程x^2/m^2+y^2/(m^2-a^2)=1。

圆的圆心坐标(b,c)半径r。圆的方程(x-b)^2+(y-c)^2=r^2。

线段AB如果和圆相交最小值就是2m。

椭圆和圆相切有重根。

圆方程换元
x=b+r*2t/(1+t^2)
y=c+r*(1-t^2/(1+t^2)

带入椭圆方程，得到：
f=m*m-a*a)*(b*(1+t*t)+2*r*t)**2+m*m*(c*(1+t*t)+r*(1-t*t))**2-m*m*(m*m-a*a)*(1+t*t)**2=0

现在就是关于m和t的多项式方程，有重根就是方程和导数方程有同根。
f是t的四次方程，对t求导得到一个t的三次方程，联立方程就可以解出来m和t。

这两个方程对于已知的abcr都不好直接解，更别说都是参数的已知条件。

我们换元的好处出来了，一个是t的四次方程一个是t的三次方程，就可以辗转相除法消去t。过程比较复杂好在有程序可以处理。

消去t后得到m的一个高次方程，好在能分解。这个分解一定有内在原因，可以找找这个分解的原因。


分解后的方程：

g=
(-a**4*b**4 + a**4*b**2*r**2 - m**8 + m**6*(2*a**2 + 2*b**2 + 2*c**2 - 2*c*r + 2*r**2) + m**4*(-a**4 - 4*a**2*b**2 - 2*a**2*c**2 + 2*a**2*c*r - 4*a**2*r**2 - b**4 - 2*b**2*c**2 + 2*b**2*c*r + b**2*r**2 - c**4 + 2*c**3*r - 2*c**2*r**2 + 2*c*r**3 - r**4) + m**2*(2*a**4*b**2 + 2*a**4*r**2 + 2*a**2*b**4 + 2*a**2*b**2*c**2 - 2*a**2*b**2*c*r - 2*a**2*b**2*r**2 + 2*a**2*c**2*r**2 - 4*a**2*c*r**3 + 2*a**2*r**4))**2

*(a**8*b**4 - 2*a**8*b**2*r**2 + a**8*r**4 - 2*a**6*b**6 + 2*a**6*b**4*c**2 + 6*a**6*b**4*r**2 - 4*a**6*b**2*c**2*r**2 - 6*a**6*b**2*r**4 + 2*a**6*c**2*r**4 + 2*a**6*r**6 + a**4*b**8 + 2*a**4*b**6*c**2 - 4*a**4*b**6*r**2 + a**4*b**4*c**4 - 6*a**4*b**4*c**2*r**2 + 6*a**4*b**4*r**4 - 2*a**4*b**2*c**4*r**2 + 6*a**4*b**2*c**2*r**4 - 4*a**4*b**2*r**6 + a**4*c**4*r**4 - 2*a**4*c**2*r**6 + a**4*r**8 + m**8*(a**4 - 2*a**2*b**2 + 2*a**2*c**2 + b**4 + 2*b**2*c**2 + c**4) + m**6*(-2*a**6 + 2*a**4*b**2 - 6*a**4*c**2 - 4*a**4*r**2 + 2*a**2*b**4 - 4*a**2*b**2*c**2 + 6*a**2*b**2*r**2 - 6*a**2*c**4 - 6*a**2*c**2*r**2 - 2*b**6 - 6*b**4*c**2 - 2*b**4*r**2 - 6*b**2*c**4 - 4*b**2*c**2*r**2 - 2*c**6 - 2*c**4*r**2) + m**4*(a**8 + 2*a**6*b**2 + 4*a**6*c**2 + 6*a**6*r**2 - 6*a**4*b**4 + 8*a**4*b**2*c**2 - 8*a**4*b**2*r**2 + 6*a**4*c**4 + 10*a**4*c**2*r**2 + 6*a**4*r**4 + 2*a**2*b**6 + 8*a**2*b**4*c**2 + 4*a**2*b**4*r**2 + 10*a**2*b**2*c**4 + 6*a**2*b**2*c**2*r**2 - 6*a**2*b**2*r**4 + 4*a**2*c**6 + 2*a**2*c**4*r**2 + 6*a**2*c**2*r**4 + b**8 + 4*b**6*c**2 - 2*b**6*r**2 + 6*b**4*c**4 - 6*b**4*c**2*r**2 + b**4*r**4 + 4*b**2*c**6 - 6*b**2*c**4*r**2 + 2*b**2*c**2*r**4 + c**8 - 2*c**6*r**2 + c**4*r**4) + m**2*(-2*a**8*b**2 - 2*a**8*r**2 + 2*a**6*b**4 - 6*a**6*b**2*c**2 + 4*a**6*b**2*r**2 - 6*a**6*c**2*r**2 - 6*a**6*r**4 + 2*a**4*b**6 - 4*a**4*b**4*c**2 - 8*a**4*b**4*r**2 - 6*a**4*b**2*c**4 + 6*a**4*b**2*c**2*r**2 + 10*a**4*b**2*r**4 - 6*a**4*c**4*r**2 - 2*a**4*c**2*r**4 - 4*a**4*r**6 - 2*a**2*b**8 - 6*a**2*b**6*c**2 + 6*a**2*b**6*r**2 - 6*a**2*b**4*c**4 + 10*a**2*b**4*c**2*r**2 - 6*a**2*b**4*r**4 - 2*a**2*b**2*c**6 + 2*a**2*b**2*c**4*r**2 - 2*a**2*b**2*c**2*r**4 + 2*a**2*b**2*r**6 - 2*a**2*c**6*r**2 + 4*a**2*c**4*r**4 - 2*a**2*c**2*r**6))

=0


分解成了两个偶数次的8次因子，有一个还是2次幂，相当于两个4次方程了，就可以正常求解了。

求出来的正根m如果带入方程t有实数解，那就是一个符合的切点。所有符合的切点m的最大最小值就是所求的最大最小值。

此方法很多光滑曲线距离问题或者说相切问题都可以。


Python代码如下：

# 曲线相切问题 copy by yuange 2023.10.22
from sympy import *
rn="\r\n"
a,b,c,r,t=symbols('a b c r t',real=True)
m=symbols('m',positive=True)
f=(m*m-a*a)*(b*(1+t*t)+2*r*t)**2+m*m*(c*(1+t*t)+r*(1-t*t))**2-m*m*(m*m-a*a)*(1+t*t)**2
g=diff(f,t)/4
re,h=div(f,g,t)
h1,h2=fraction(cancel(h))
re,i=div(g,h1,t)
i1,i2=fraction(cancel(i))
re,j=div(h,i1,t)
j1,j2=fraction(cancel(j))

jf=collect(factor(j1),m)
print(rn,rn,"jf=",jf)

j=jf.evalf().subs({a:2.5,b:0.7,c:2.4,r:6})

print(rn,rn,"j=",j)
res=solve(j,m)
print(rn,"ok!",res)


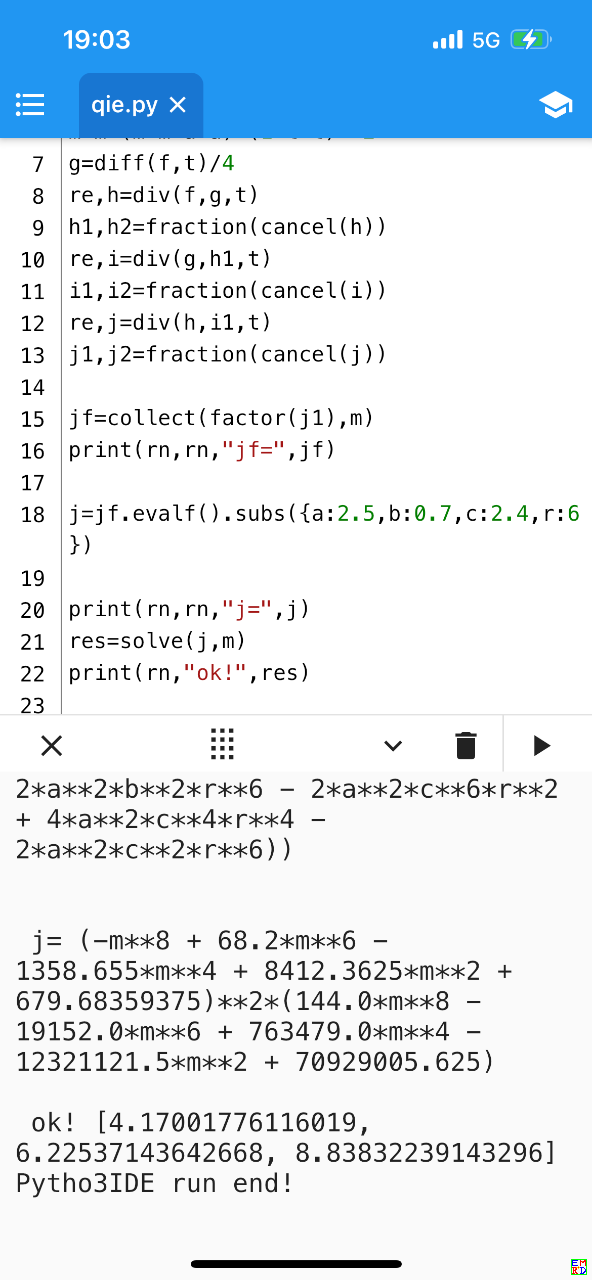
最后带入这图中题目数据，得到m的方程为：
j= (-m**8 + 68.2*m**6 - 1358.655*m**4 + 8412.3625*m**2 + 679.68359375)**2*(144.0*m**8 - 19152.0*m**6 + 763479.0*m**4 - 12321121.5*m**2 + 70929005.625)

可以解方程求出精确解，数值解为：

ok! [4.17001776116019, 6.22537143642668, 8.83832239143296]
Pytho3IDE run end!



结果三个相切情况，距离最大最小17..68和8.34。



这题做出来通解还是有些难度的，没有数据的通解太复杂了。所幸有程序可以帮着处理一些数据，辗转相除没有程序手工不可能做出来，还有最后的分解。

拉格朗日系数法、切线法等方法可以得到两个方程，最后要得到m的直接方程的形式也是很复杂的。

换元得到多项式形式导数低一次就辗转相除可以消元。

这方法距离之差双曲线等两曲线相切别的很多情况，都可以这么做。

yuange1975

线段AB如果和圆相交最小值就是2m。

是

线段AB如果和圆相交最小值就是2a。






修改一下程序代码打印图中距离最大最小值的方程和精确根以及化简和数值解。

j=jf.subs({a:25,b:7,c:24,r:60})

j=j.subs(m,5*m)
j=j/factor_list(j)[0]
j=factor(j)

print(rn,rn,"j=",j)
m1,m2,m3=solve(j,m)
m1=simplify(m1)
m2=simplify(m2)
m3=simplify(m3)

print(rn,"ok!",rn,rn,m1,rn,rn,m2,rn,rn,m3)

print(rn,rn,m1.evalf(),rn,rn,m2.evalf(),rn,rn,m3.evalf())

四次方程根表达式太复杂了，结果如下：


j= (m**8 - 532*m**6 + 84831*m**4 - 5476054*m**2 + 126096010)*(25*m**8 - 6820*m**6 + 543462*m**4 - 13459780*m**2 - 4349975)**2

ok!

sqrt(6*sqrt(3)*(-200759 + 24976*sqrt(223))**(1/6)*(-4623 + (-200759 + 24976*sqrt(223))**(2/3) + 526*(-200759 + 24976*sqrt(223))**(1/3))**(3/4) + 6*sqrt(3)*(-200759 + 24976*sqrt(223))**(1/6)*sqrt(-(-200759 + 24976*sqrt(223))**(2/3)*sqrt(-4623 + (-200759 + 24976*sqrt(223))**(2/3) + 526*(-200759 + 24976*sqrt(223))**(1/3)) + 4623*sqrt(-4623 + (-200759 + 24976*sqrt(223))**(2/3) + 526*(-200759 + 24976*sqrt(223))**(1/3)) + 1052*(-200759 + 24976*sqrt(223))**(1/3)*sqrt(-4623 + (-200759 + 24976*sqrt(223))**(2/3) + 526*(-200759 + 24976*sqrt(223))**(1/3)) + 14256*sqrt(3)*sqrt(-200759 + 24976*sqrt(223))) + 532*(-200759 + 24976*sqrt(223))**(1/3)*(-4623 + (-200759 + 24976*sqrt(223))**(2/3) + 526*(-200759 + 24976*sqrt(223))**(1/3))**(1/4))/(2*(-200759 + 24976*sqrt(223))**(1/6)*(-4623 + (-200759 + 24976*sqrt(223))**(2/3) + 526*(-200759 + 24976*sqrt(223))**(1/3))**(1/8))

sqrt(-6*sqrt(3)*(-200759 + 24976*sqrt(223))**(1/6)*sqrt(-(-200759 + 24976*sqrt(223))**(2/3)*sqrt(-4623 + (-200759 + 24976*sqrt(223))**(2/3) + 526*(-200759 + 24976*sqrt(223))**(1/3)) + 4623*sqrt(-4623 + (-200759 + 24976*sqrt(223))**(2/3) + 526*(-200759 + 24976*sqrt(223))**(1/3)) + 1052*(-200759 + 24976*sqrt(223))**(1/3)*sqrt(-4623 + (-200759 + 24976*sqrt(223))**(2/3) + 526*(-200759 + 24976*sqrt(223))**(1/3)) + 14256*sqrt(3)*sqrt(-200759 + 24976*sqrt(223))) + 6*sqrt(3)*(-200759 + 24976*sqrt(223))**(1/6)*(-4623 + (-200759 + 24976*sqrt(223))**(2/3) + 526*(-200759 + 24976*sqrt(223))**(1/3))**(3/4) + 532*(-200759 + 24976*sqrt(223))**(1/3)*(-4623 + (-200759 + 24976*sqrt(223))**(2/3) + 526*(-200759 + 24976*sqrt(223))**(1/3))**(1/4))/(2*(-200759 + 24976*sqrt(223))**(1/6)*(-4623 + (-200759 + 24976*sqrt(223))**(2/3) + 526*(-200759 + 24976*sqrt(223))**(1/3))**(1/8))

CRootOf(25*m**8 - 6820*m**6 + 543462*m**4 - 13459780*m**2 - 4349975, 1)


17.6766447828659

8.34003552232038

12.4507428728534

王守恩

我只会凑答案。

1. N[Minimize[{Sqrt[3^2+6^2-2*3*6Sin[a]]+Sqrt[4^2+6^2-2*4*6Cos[a]]},{a}],20]

复制代码

{8.3400355223203758019, {a -> 0.31376767216683659600}}

yuange1975

一些求极值的题目，最后导数解方程是高次不好解或者解后比较复杂，最后极值表达式很复杂。可以先得到极值方程，再求解。

之前我发过方法，极值方程我都是用的待定系数法解方程。现在这个另外一种方法来了，用换元换成多项式后，可以用辗转相除法消元，然后就可以得到极值方程了。

其实这个帖子虽然利用了数学软件，还真不是数学软件的事情，不是简单一个函数就出来了。如果不是通解，具体数值的问题，不用软件辗转相除结果完全可以自己算出来。通用结果看那一堆，确实是没有软件基本上做不到。


这些解题思路，以及通用解决这一类问题的方法，这才是重点。后面可以去把我的计算极值的代码再优化成辗转相除法的，

曹半

思路提示：阿波罗尼斯圆