- 注册时间
- 2021-11-19
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 9975
- 在线时间
- 小时
|
马上注册,结交更多好友,享用更多功能,让你轻松玩转社区。
您需要 登录 才可以下载或查看,没有账号?欢迎注册
×
本帖最后由 nyy 于 2024-5-11 09:03 编辑
- Clear["Global`*"];
- ans=Solve[{
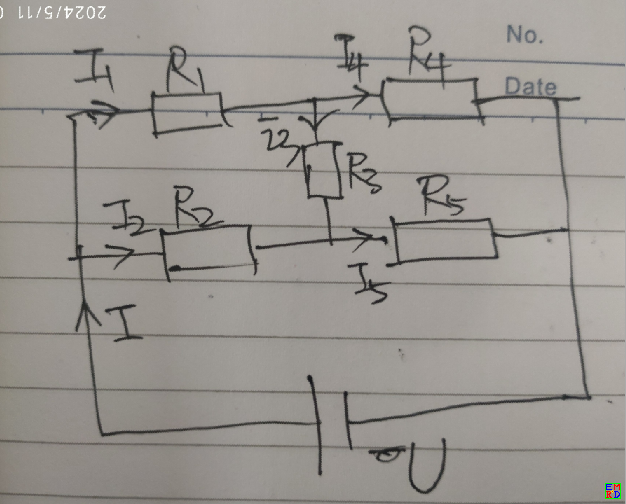
- i==i1+i2==i4+i5,
- i1==i3+i4,
- i2+i3==i5,
- U==i2*R2+i5*R5,
- i1*R1+i3*R3==i2*R2,
- i3*R3+i5*R5==i4*R4
- },{i,i1,i2,i3,i4,i5}]
- Grid[Transpose@ans,Alignment->Left](*列表显示*)
求解结果。
\[\begin{array}{l}
i\to \frac{U (\text{R1} \text{R3}+\text{R1} \text{R4}+\text{R1} \text{R5}+\text{R2} \text{R3}+\text{R2} \text{R4}+\text{R2} \text{R5}+\text{R3} \text{R4}+\text{R3} \text{R5})}{\text{R1} \text{R2} \text{R3}+\text{R1} \text{R2} \text{R4}+\text{R1} \text{R2} \text{R5}+\text{R1} \text{R3} \text{R5}+\text{R1} \text{R4} \text{R5}+\text{R2} \text{R3} \text{R4}+\text{R2} \text{R4} \text{R5}+\text{R3} \text{R4} \text{R5}} \\
\text{i1}\to \frac{U (\text{R2} \text{R3}+\text{R2} \text{R4}+\text{R2} \text{R5}+\text{R3} \text{R5})}{\text{R1} \text{R2} \text{R3}+\text{R1} \text{R2} \text{R4}+\text{R1} \text{R2} \text{R5}+\text{R1} \text{R3} \text{R5}+\text{R1} \text{R4} \text{R5}+\text{R2} \text{R3} \text{R4}+\text{R2} \text{R4} \text{R5}+\text{R3} \text{R4} \text{R5}} \\
\text{i2}\to \frac{U (\text{R1} \text{R3}+\text{R1} \text{R4}+\text{R1} \text{R5}+\text{R3} \text{R4})}{\text{R1} \text{R2} \text{R3}+\text{R1} \text{R2} \text{R4}+\text{R1} \text{R2} \text{R5}+\text{R1} \text{R3} \text{R5}+\text{R1} \text{R4} \text{R5}+\text{R2} \text{R3} \text{R4}+\text{R2} \text{R4} \text{R5}+\text{R3} \text{R4} \text{R5}} \\
\text{i3}\to -\frac{U (\text{R1} \text{R5}-\text{R2} \text{R4})}{\text{R1} \text{R2} \text{R3}+\text{R1} \text{R2} \text{R4}+\text{R1} \text{R2} \text{R5}+\text{R1} \text{R3} \text{R5}+\text{R1} \text{R4} \text{R5}+\text{R2} \text{R3} \text{R4}+\text{R2} \text{R4} \text{R5}+\text{R3} \text{R4} \text{R5}} \\
\text{i4}\to \frac{U (\text{R1} \text{R5}+\text{R2} \text{R3}+\text{R2} \text{R5}+\text{R3} \text{R5})}{\text{R1} \text{R2} \text{R3}+\text{R1} \text{R2} \text{R4}+\text{R1} \text{R2} \text{R5}+\text{R1} \text{R3} \text{R5}+\text{R1} \text{R4} \text{R5}+\text{R2} \text{R3} \text{R4}+\text{R2} \text{R4} \text{R5}+\text{R3} \text{R4} \text{R5}} \\
\text{i5}\to \frac{U (\text{R1} \text{R3}+\text{R1} \text{R4}+\text{R2} \text{R4}+\text{R3} \text{R4})}{\text{R1} \text{R2} \text{R3}+\text{R1} \text{R2} \text{R4}+\text{R1} \text{R2} \text{R5}+\text{R1} \text{R3} \text{R5}+\text{R1} \text{R4} \text{R5}+\text{R2} \text{R3} \text{R4}+\text{R2} \text{R4} \text{R5}+\text{R3} \text{R4} \text{R5}} \\
\end{array}\]
尤其是这个结果
i3 -> -(((-R2 R4 + R1 R5) U)/(
R1 R2 R3 + R1 R2 R4 + R2 R3 R4 + R1 R2 R5 + R1 R3 R5 + R1 R4 R5 + R2 R4 R5 + R3 R4 R5))
上面用了基尔霍夫电流电压定律,就不注释了,还算比较简单! |
-
|