绘制出分叉和混沌图后，如何精确求解分叉位置？

Jack315

再迭代一次……

1. p6 = Collect[f[\[Mu], p5], \[Mu]]

复制代码

由于多项式项数的增加，参变量 \(\mu\) 的最高幂次也达到了 63 。
作图时，数值精度也采用了 100 位。
若要再进一步，恐怕软件也无能为力了。

作图代码：

1. Plot[{p0, p1, p2, p3, p4, p5, p6},
   
2. {\[Mu], 0, 2},
   
3. WorkingPrecision -> 100,
   
4. PlotLegends -> "Expressions",
   
5. PlotLabel -> "暗线",
   
6. GridLines -> Automatic,
   
7. Frame -> True]

复制代码

\(1.4\le\mu\le 2.0\) 部分的放大图：


\(1.8\le\mu\le 2.0\) 部分的放大图：

wayne

设$f(c,x)=x(c-x)$, 当存在二分叉的时候,就是 $f(c,x_1)=x_2,f(c,x_2)=x_1$, 算得 $x_{1,2} = \frac{1}{2} (c+1+-\sqrt{(c-3) (c+1)})$, 于是 $c>3$
二分叉的代码

1. data=Block[{c=34/10},NestWhileList[#(c-#)&,RandomReal[]*c,Abs[#1-#3]>10^-20&,3,10000]]

复制代码

四分叉的代码

1. data=Block[{c=35/10},NestWhileList[#(c-#)&,RandomReal[]*c,Abs[#1-#5]>10^-20&,5,10000]]

复制代码

对$f(c,x_1)=x_2,f(c,x_2)=x_3,f(c,x_3)=x,f(c,x)=x_1$消元,得到$1+c^2-c x-c^2 x-c^3 x-c^4 x+2 c x^2+c^2 x^2+4 c^3 x^2+c^4 x^2+2 c^5 x^2-x^3-5 c^2 x^3-4 c^3 x^3-5 c^4 x^3-4 c^5 x^3-c^6 x^3+2 c x^4+6 c^2 x^4+4 c^3 x^4+14 c^4 x^4+5 c^5 x^4+3 c^6 x^4-4 c x^5-c^2 x^5-18 c^3 x^5-12 c^4 x^5-12 c^5 x^5-3 c^6 x^5+x^6+10 c^2 x^6+17 c^3 x^6+18 c^4 x^6+15 c^5 x^6+c^6 x^6-2 c x^7-14 c^2 x^7-12 c^3 x^7-30 c^4 x^7-6 c^5 x^7+6 c x^8+3 c^2 x^8+30 c^3 x^8+15 c^4 x^8-x^9-15 c^2 x^9-20 c^3 x^9+3 c x^10+15 c^2 x^10-6 c x^11+x^12$, 再令导数未=为0,消元得到$3375+1980 c^2-412 c^3-1073 c^4-8 c^5+84 c^6+376 c^7-191 c^8-40 c^9+48 c^10-12 c^11+c^12=0$, 存在一根$\sqrt{6}+1 = 3.4494897427831780982$

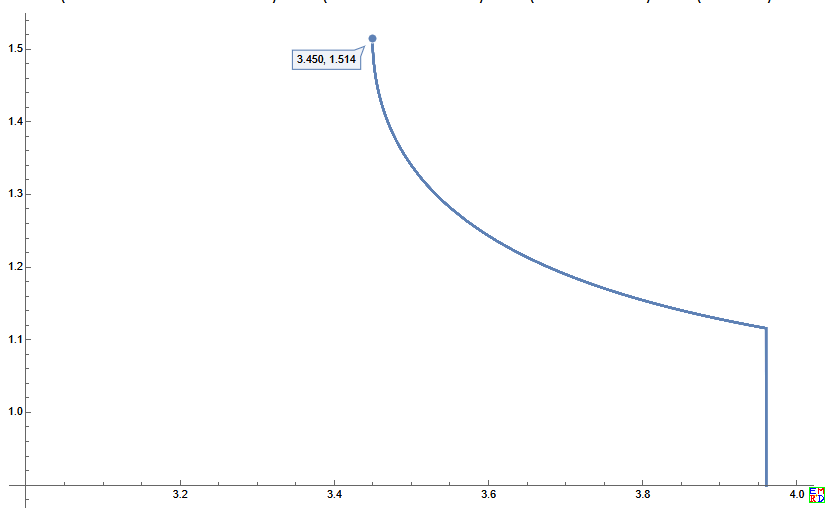
1. Plot[Root[1+c^2+(-c-c^2-c^3-c^4) #1+(2 c+c^2+4 c^3+c^4+2 c^5) #1^2+(-1-5 c^2-4 c^3-5 c^4-4 c^5-c^6) #1^3+(2 c+6 c^2+4 c^3+14 c^4+5 c^5+3 c^6) #1^4+(-4 c-c^2-18 c^3-12 c^4-12 c^5-3 c^6) #1^5+(1+10 c^2+17 c^3+18 c^4+15 c^5+c^6) #1^6+(-2 c-14 c^2-12 c^3-30 c^4-6 c^5) #1^7+(6 c+3 c^2+30 c^3+15 c^4) #1^8+(-1-15 c^2-20 c^3) #1^9+(3 c+15 c^2) #1^10-6 c #1^11+#1^12&,1]&/@Range[12],{c,3,4}]

复制代码

wayne

同理,三叉点的情况

1. f[c_,x_]:=x(c-x);GroebnerBasis[{f[c,x1]==x2,f[c,x2]==x,f[c,x]==x1},{},{x1,x2}]//Factor

复制代码

设$f(c,x)=x(c-x)$, 当存在三分叉的时候,就是 $f(c,x_1)=x_2,f(c,x_2)=x_3,f(c,x_3)=x_1$, 算得 $x_{1,2,3}$是方程$1-x-c^3 (-1+x)^2 x+x^2-x^3+x^4-x^5+x^6+c^2 (-1+x) (-1+x-2 x^2+3 x^3)-c (-1+x) (1-x+2 x^2-x^3+3 x^4)=0$的三个实根.
联立导数为0,消元得到 $-49-28 c-18 c^2+24 c^3+4 c^4-6 c^5+c^6 = 0$,存在一根$c_1= 1+2\sqrt{2}= 3.8284271247461900976$

参考链接: https://mathworld.wolfram.com/LogisticMap.html

1. Plot[Root[1+c+c^2+(-1-2 c-2 c^2-c^3) #1+(1+3 c+3 c^2+2 c^3) #1^2+(-1-3 c-5 c^2-c^3) #1^3+(1+4 c+3 c^2) #1^4+(-1-3 c) #1^5+#1^6&,#]&/@Range[6],{c,3.5,4}]

复制代码

wayne

写了个代码,直接计算$n$分叉点的位置

1. n=5;orig=FactorList[Factor[Nest[#(c-#)&,x,n]-x]][[All,1]];
   
2. exp=Factor[First@SolveValues[Dt[orig[[-1]]]==0,Dt[c]]/Dt[x]];
   
3. Solve[First@GroebnerBasis[{Numerator[exp]==0,orig[[-1]]==0},{},{x}]==0&&c>3,c]

复制代码

Jack315

【分岔点计算】
计算方法参考：https://mathworld.wolfram.com/LogisticMap.html

• 求周期 n 的迭代方程。
• 求迭代方程的判别式：随着参数值的增加，迭代方程的一对根从复根变成相等的实根，从而出现分岔。
• 求判别式的根即得到分岔处的参数值。
  

映射函数：\(f(r,x)=x(r-x)\)

1. f[r_, x_] := x (r - x)

复制代码

分岔图：

参数值范围更大的分岔图：

Jack315

【周期 1 轨道】
迭代方程：

1. f1[r_, x_] :=
   
2. Nest[f[r, #] - t &, t, 1] /. t -> x // Expand // Simplify

复制代码

判别式：

1. d1 = Factor[Discriminant[f1[r, x], x]]

复制代码

判别式根：

1. Solve[d1 == 0, r]

复制代码

周期 1 轨道从 \(r_1=1\) 处开始。

Jack315

【周期 2】
迭代方程：

1. f2[r_, x_] := (Nest[f[r, #] &, t, 2] - t)/(f[r, t] - t) /. t -> x // Expand // Simplify

复制代码

判别式：

1. d2 = Factor[Discriminant[f2[r, x], x]]

复制代码

判别式根：

1. Solve[d2 == 0, r]

复制代码

周期 2 分岔点参数：\(r_2=3\) 。

Jack315

【周期 3】
迭代方程：

1. f3[r_, x_] := (Nest[f[r, #] &, t, 3] - t)/(f[r, t] - t) /. t -> x // Expand // Simplify

复制代码

判别式：

1. d2 = Factor[Discriminant[f2[r, x], x]]

复制代码

判别式根：

1. Solve[d3 == 0, r]

复制代码

周期 3 分岔点参数：\(r_3=1+2\sqrt{2}=3.828427125\) 。

Jack315

【周期 4】
迭代方程：

1. f4[r_, x_] := (Nest[f[r, #] &, t, 4] - t)/(Nest[f[r, #] &, t, 2] - t) /. t -> x // Expand // Simplify

复制代码

判别式：

1. d4 = Factor[Discriminant[f4[r, x], x]]

复制代码

判别式根：

1. Solve[d4 == 0, r]

复制代码

周期 4 分岔点参数：\(r_4=1+\sqrt{6}=3.449489743, 3.960101883\) 。

Jack315

【周期 5】
迭代方程：

1. f5[r_, x_] := (Nest[f[r, #] &, t, 5] - t)/(Nest[f[r, #] &, t, 1] - t) /. t -> x // Expand // Simplify

复制代码

判别式：

1. d5 = Factor[Discriminant[f5[r, x], x]]

复制代码

判别式根：

1. Solve[d5 == 0, r]

复制代码

周期 5 分岔点参数：\(r_5=3.738172375, 3.905571870, 3.990257307\) 。