- 注册时间
- 2020-8-25
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 1053
- 在线时间
- 小时
|
 发表于 2024-9-21 17:04:07
|
显示全部楼层
发表于 2024-9-21 17:04:07
|
显示全部楼层
本帖最后由 yigo 于 2024-9-21 18:22 编辑
找到了递推公式后,发现有简单的证明方法。
偶数情况:2m个排成一排的硬币,各个位置的正反面,满足没有两个连续正面,且从中挑出1,3,5,...2m-1位置的硬币依次排成一排,也没有两个连续正面的可能情况数设为C(m),
如果2m-1位是正面,那么2m,2m-2,2m-3位置必须是反面,剩下位置满足要求的恰好是C(m-2),
如果2m-1位是反面,那么2m-1位置前面的可能情况是C(m-1),而2m位置正反均可2种情况,故总计是2C(m-1),所以C(m)=2C(m-1)+C(m-2),
奇数情况:2m-1个排成一排的硬币,各个位置的正反面,满足没有两个连续正面,且从中挑出1,3,5,...2m-1位置的硬币依次排成一排,也没有两个连续正面的可能情况数设为E(m),
如果2m-1位是正面,那么情况数是 C(m-2),
如果2m-1位是反面,那么情况数是 C(m-1),所以E(m)=C(m-1)+C(m-2),所以E(m)也满足E(m)=2E(m-1)+E(m-2)的递推关系。
-------------------------------------
这种套娃还挺有意思的,在来个例子,
偶数情况:2m个排成一排的硬币,各个位置的正反面,满足没有两个连续正面,且从中挑出奇数位置、偶数位置各自分别排成一排,也没有两个连续正面的可能情况数设为S(m),
奇数情况:2m-1个排成一排的硬币,各个位置的正反面,满足没有两个连续正面,且从中挑出奇数位置、偶数位置各自分别排成一排,也没有两个连续正面的可能情况数设为R(m),
则有:S(m)=R(m)+R(m-1),R(m)=S(m-1)+S(m-2)
-----------------------------------
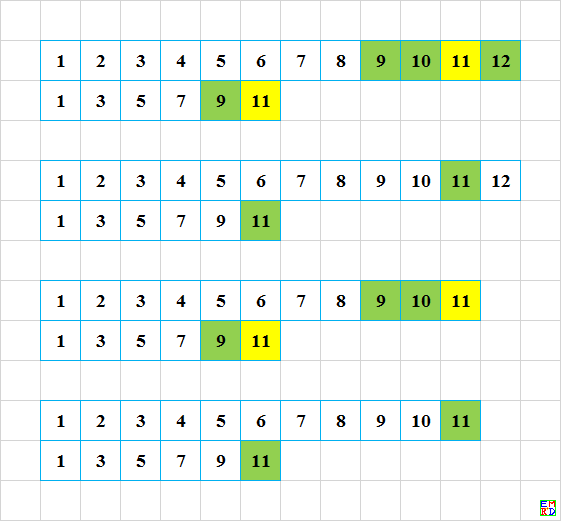
看图理解:
1
|
|