- 注册时间
- 2021-11-19
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 9984
- 在线时间
- 小时
|
 发表于 2025-2-14 13:25:54
|
显示全部楼层
发表于 2025-2-14 13:25:54
|
显示全部楼层
无数组解就对了,因为我找到了无数组解了!
上图片。
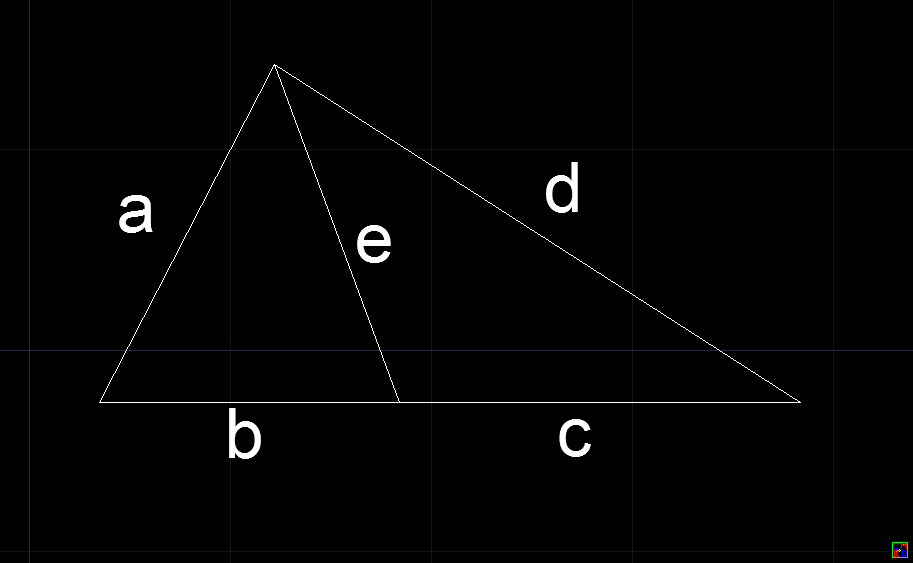
上代码:
- Clear["Global`*"];(*mathematica11.2,win7(64bit)Clear all variables*)
- (*子函数,海伦公式,利用海伦公式计算三角形的面积*)
- heron[a_,b_,c_]:=Module[{p=(a+b+c)/2},Sqrt[p*(p-a)*(p-b)*(p-c)]]
- (*子函数,利用三边计算角的余弦值,角是c边所对的角*)
- cs[a_,b_,c_]:=((a^2+b^2-c^2)/(2*a*b))
- (*赋值*)
- p1=1/2*(a+b+e)(*左边三角形的半周长*)
- p2=1/2*(c+d+e)(*右边三角形的半周长*)
- p=(a+b+c+d)/2(*大三角形的半周长*)
- r1=2*heron[a,b,e]/p1(*左边小三角形的半径*)
- r2=2*heron[c,d,e]/p2(*右边小三角形的半径*)
- r=2*heron[a,b+c,d]/p(*最大三角形的半径*)
- h=heron[a,b,e]/(b/2)(*三角形的高*)
- (*列出方程,为方便迭代,把方程尽可能地多项式化*)
- eq1=Numerator@Together[r1^2-r2^2](*两个小圆半径相等*)
- eq2=Numerator@Together[cs[b,e,a]+cs[c,e,d]](*两个角相加=180,则余弦值的和=零*)
- eq3=p1-b-5(*AE=5*)
- eq4=p-(b+c)-4(*AD=4*)
- eqns={eq1,eq2,eq3,eq4}(*形成方程组*)
- ans=Solve[eqns==0,{a,b,c,d,e},Method->Reduce]
- Grid[ans,Alignment->Left](*列表显示*)
- GF=p2-d/.ans[[2]](*计算GF的长度*)
- (*给出当e=8时的长度*)
- aaa=Solve[eqns==0&&a>0&&b>0&&c>0&&d>0&&e>0&&e==8,{a,b,c,d,e},Method->Reduce]
思路全部在注释里面
求解结果
\[\begin{array}{lllll}
a\to \frac{30-e}{6} & b\to \frac{5 (e-6)}{6} & c\to \frac{-e^2+7 e-6}{2 (e-3)} & d\to \frac{e^2-3 e+6}{2 (e-3)} & \text{} \\
a\to \frac{e+20}{4} & b\to \frac{5 (e-4)}{4} & c\to \frac{1}{4} \left(e^2-5 e+4\right) & d\to \frac{1}{4} \left(e^2-e-4\right) & \text{} \\
a\to b+9 & c\to 0 & d\to -1 & e\to 1 & \text{} \\
a\to b+5 & c\to 1 & d\to 4 & e\to 5 & \text{} \\
a\to \frac{11}{2} & b\to -\frac{5}{2} & c\to -\frac{1}{2} & d\to -\frac{1}{2} & e\to 2 \\
\end{array}\]
只有第二行的解是有用的,是
\[\left\{a\to \frac{e+20}{4},b\to \frac{5 (e-4)}{4},c\to \frac{1}{4} \left(e^2-5 e+4\right),d\to \frac{1}{4} \left(e^2-e-4\right)\right\}\]
计算GF的长度,等于1,
列举出其中的一个解
{{a -> 7, b -> 5, c -> 7, d -> 13, e -> 8}}
|
|