求CD的长度？

nyy

不知道为什么，现在初中的题目这么难

aimisiyou

（8+4√13)/3

nyy

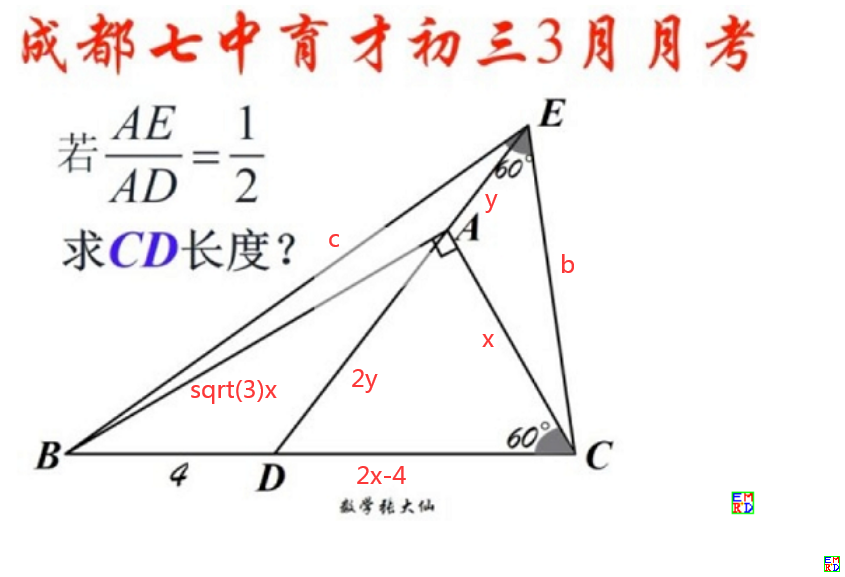
1. Clear["Global`*"];(*mathematica11.2,win7(64bit)Clear all variables*)
   
2. deg=Pi/180;(*角度制下1°所对应的弧度*)
   
3. (*子函数,利用三边计算角的余弦值,角是c边所对的角*)
   
4. cs[a_,b_,c_]:=((a^2+b^2-c^2)/(2*a*b))
   
5. ans=Solve[{
   
6.     (*∠BDE+∠CDE=180°,因此余弦值相加等于零*)
   
7.     Numerator@Together[cs[4,2*y,Sqrt[3]*x]+cs[2*x-4,2y,x]],
   
8.     (*∠BDA+∠CDA=180°,因此余弦值相加等于零*)
   
9.     Numerator@Together[cs[4,3y,c]+cs[2x-4,3y,b]],
   
10.     (*对∠BEC使用余弦定理*)
    
11.     Numerator@Together[cs[b,c,2x]-Cos[60deg]],
    
12.     (*∠BAE+∠CAE=270°,因此余弦值的平方和相加等于1*)
    
13.     Numerator@Together[cs[Sqrt[3]*x,y,c]^2+cs[x,y,b]^2-1]
    
14. }==0,{x,y,b,c}]//FullSimplify//ToRadicals;
    
15. Grid[ans,Alignment->Left](*列表显示*)
    
16. aaa=Select[ans,(And[x>=0,y>=0,b>=0,c>=0]/.#)&](*过滤出非负数解*)
    
17. Grid[aaa,Alignment->Left](*列表显示*)
    
18. Grid[N@aaa,Alignment->Left](*数值列表显示*)
    
19. bbb=(2x-4)/.aaa//Simplify
    

复制代码

方程组的全部解为
\[\begin{array}{|l|l|l|l|}
\hline
x\to 0 & y\to 0 & b\to 0 & c\to 0 \\
\hline
x\to 2-\frac{2 i}{\sqrt{3}} & y\to 0 & b\to -4 \sqrt{\frac{2}{3}} & c\to 4 (-1)^{5/6} \sqrt{2} \\
\hline
x\to 2-\frac{2 i}{\sqrt{3}} & y\to 0 & b\to 4 \sqrt{\frac{2}{3}} & c\to -4 (-1)^{5/6} \sqrt{2} \\
\hline
x\to 2-\frac{2 i}{\sqrt{3}} & y\to 0 & b\to \sqrt{-\frac{16}{21}-\frac{1}{7} 16 i \sqrt{3}} & c\to -4 \sqrt{\frac{4}{7}-\frac{2 i \sqrt{3}}{7}} \\
\hline
x\to 2-\frac{2 i}{\sqrt{3}} & y\to 0 & b\to -\sqrt{-\frac{16}{21}-\frac{1}{7} 16 i \sqrt{3}} & c\to 4 \sqrt{\frac{4}{7}-\frac{2 i \sqrt{3}}{7}} \\
\hline
x\to 2+\frac{2 i}{\sqrt{3}} & y\to 0 & b\to -4 \sqrt{\frac{2}{3}} & c\to -4 \sqrt[6]{-1} \sqrt{2} \\
\hline
x\to 2+\frac{2 i}{\sqrt{3}} & y\to 0 & b\to 4 \sqrt{\frac{2}{3}} & c\to 4 \sqrt[6]{-1} \sqrt{2} \\
\hline
x\to 2+\frac{2 i}{\sqrt{3}} & y\to 0 & b\to \sqrt{-\frac{16}{21}+\frac{16 i \sqrt{3}}{7}} & c\to -4 \sqrt{\frac{4}{7}+\frac{2 i \sqrt{3}}{7}} \\
\hline
x\to 2+\frac{2 i}{\sqrt{3}} & y\to 0 & b\to -\sqrt{-\frac{16}{21}+\frac{16 i \sqrt{3}}{7}} & c\to 4 \sqrt{\frac{2}{7} \left(2+i \sqrt{3}\right)} \\
\hline
x\to \frac{1}{3} (-2) \left(\sqrt{13}-5\right) & y\to -2 \sqrt{\frac{1}{3} \left(5-\sqrt{13}\right)} & b\to \frac{1}{3} (-4) \left(\sqrt{13}-2\right) & c\to 6-2 \sqrt{13} \\
\hline
x\to \frac{1}{3} (-2) \left(\sqrt{13}-5\right) & y\to \sqrt{\frac{2}{3} \left(10-2 \sqrt{13}\right)} & b\to \frac{1}{3} (-4) \left(\sqrt{13}-2\right) & c\to 6-2 \sqrt{13} \\
\hline
x\to \frac{1}{3} (-2) \left(\sqrt{13}-5\right) & y\to -2 \sqrt{\frac{1}{3} \left(5-\sqrt{13}\right)} & b\to \frac{4}{3} \left(\sqrt{13}-2\right) & c\to 2 \left(\sqrt{13}-3\right) \\
\hline
x\to \frac{1}{3} (-2) \left(\sqrt{13}-5\right) & y\to \sqrt{\frac{2}{3} \left(10-2 \sqrt{13}\right)} & b\to \frac{4}{3} \left(\sqrt{13}-2\right) & c\to 2 \left(\sqrt{13}-3\right) \\
\hline
x\to \frac{2}{3} \left(\sqrt{13}+5\right) & y\to -2 \sqrt{\frac{1}{3} \left(\sqrt{13}+5\right)} & b\to \frac{1}{3} (-4) \left(\sqrt{13}+2\right) & c\to -2 \left(\sqrt{13}+3\right) \\
\hline
x\to \frac{2}{3} \left(\sqrt{13}+5\right) & y\to 2 \sqrt{\frac{1}{3} \left(\sqrt{13}+5\right)} & b\to \frac{1}{3} (-4) \left(\sqrt{13}+2\right) & c\to -2 \left(\sqrt{13}+3\right) \\
\hline
x\to \frac{2}{3} \left(\sqrt{13}+5\right) & y\to -2 \sqrt{\frac{1}{3} \left(\sqrt{13}+5\right)} & b\to \frac{4}{3} \left(\sqrt{13}+2\right) & c\to 2 \left(\sqrt{13}+3\right) \\
\hline
x\to \frac{2}{3} \left(\sqrt{13}+5\right) & y\to 2 \sqrt{\frac{1}{3} \left(\sqrt{13}+5\right)} & b\to \frac{4}{3} \left(\sqrt{13}+2\right) & c\to 2 \left(\sqrt{13}+3\right) \\
\hline
x\to \frac{2}{15} \left(5-i \sqrt{35}\right) & y\to -\frac{2 \sqrt[4]{-1} \sqrt{\sqrt{35}-7 i}}{\sqrt{15}} & b\to -\frac{2 \left(\sqrt{35}-i\right)}{3 \sqrt{5}} & c\to -\frac{4 i}{\sqrt{5}} \\
\hline
x\to \frac{2}{15} \left(5-i \sqrt{35}\right) & y\to 2 \sqrt{\frac{1}{15} \left(7+i \sqrt{35}\right)} & b\to -\frac{2 \left(\sqrt{35}-i\right)}{3 \sqrt{5}} & c\to -\frac{4 i}{\sqrt{5}} \\
\hline
x\to \frac{2}{15} \left(5-i \sqrt{35}\right) & y\to -\frac{2 \sqrt[4]{-1} \sqrt{\sqrt{35}-7 i}}{\sqrt{15}} & b\to \frac{2 \left(\sqrt{35}-i\right)}{3 \sqrt{5}} & c\to \frac{4 i}{\sqrt{5}} \\
\hline
x\to \frac{2}{15} \left(5-i \sqrt{35}\right) & y\to 2 \sqrt{\frac{1}{15} \left(7+i \sqrt{35}\right)} & b\to \frac{2 \left(\sqrt{35}-i\right)}{3 \sqrt{5}} & c\to \frac{4 i}{\sqrt{5}} \\
\hline
x\to \frac{2}{15} \left(5+i \sqrt{35}\right) & y\to 2 (-1)^{3/4} \sqrt{\frac{1}{15} \left(\sqrt{35}+7 i\right)} & b\to \frac{2 \left(\sqrt{35}+i\right)}{3 \sqrt{5}} & c\to -\frac{4 i}{\sqrt{5}} \\
\hline
x\to \frac{2}{15} \left(5+i \sqrt{35}\right) & y\to -2 (-1)^{3/4} \sqrt{\frac{1}{15} \left(\sqrt{35}+7 i\right)} & b\to \frac{2 \left(\sqrt{35}+i\right)}{3 \sqrt{5}} & c\to -\frac{4 i}{\sqrt{5}} \\
\hline
x\to \frac{2}{15} \left(5+i \sqrt{35}\right) & y\to 2 (-1)^{3/4} \sqrt{\frac{1}{15} \left(\sqrt{35}+7 i\right)} & b\to -\frac{2 \left(\sqrt{35}+i\right)}{3 \sqrt{5}} & c\to \frac{4 i}{\sqrt{5}} \\
\hline
x\to \frac{2}{15} \left(5+i \sqrt{35}\right) & y\to -2 (-1)^{3/4} \sqrt{\frac{1}{15} \left(\sqrt{35}+7 i\right)} & b\to -\frac{2 \left(\sqrt{35}+i\right)}{3 \sqrt{5}} & c\to \frac{4 i}{\sqrt{5}} \\
\hline
\end{array}\]

过滤非负数，得到
\[\begin{array}{llll}
x\to 0 & y\to 0 & b\to 0 & c\to 0 \\
x\to \frac{1}{3} (-2) \left(\sqrt{13}-5\right) & y\to \sqrt{\frac{2}{3} \left(10-2 \sqrt{13}\right)} & b\to \frac{4}{3} \left(\sqrt{13}-2\right) & c\to 2 \left(\sqrt{13}-3\right) \\
x\to \frac{2}{3} \left(\sqrt{13}+5\right) & y\to 2 \sqrt{\frac{1}{3} \left(\sqrt{13}+5\right)} & b\to \frac{4}{3} \left(\sqrt{13}+2\right) & c\to 2 \left(\sqrt{13}+3\right) \\
\end{array}\]
数值化得到
\[\begin{array}{llll}
x\to 0. & y\to 0. & b\to 0. & c\to 0. \\
x\to 0.929632 & y\to 1.36355 & b\to 2.14074 & c\to 1.2111 \\
x\to 5.73703 & y\to 3.38734 & b\to 7.47407 & c\to 13.2111 \\
\end{array}\]

CD的长度得到
\[\left\{-4,\frac{1}{3} (-4) \left(\sqrt{13}-2\right),\frac{4}{3} \left(\sqrt{13}+2\right)\right\}\]
由于CD>=0，因此x>=2

nyy

aimisiyou 发表于 2025-4-6 15:56
（8+4√13)/3

你是个人才，我除了余弦定理，就想不出办法了！没别的思路了

aimisiyou

nyy 发表于 2025-4-7 08:47
你是个人才，我除了余弦定理，就想不出办法了！没别的思路了

勾股定理。

nyy

aimisiyou 发表于 2025-4-7 09:46
勾股定理。

上你的详细代码
或者详细的过程！

王守恩

∠DAB=a。∠ABE=b。后面用的是正弦定理。 前面用的是角分线(不一定等分)定理。

Solve[{Sin[b] Sin[Pi/6 + a]/(Sin[Pi/6] Sin[a - b])==1/2==Sin[Pi/6 - b] Sin[Pi/6 + a]/(Sin[Pi/3] Sin[Pi/3 - a + b]), Sqrt[3]*CD/Cos[a]==4/Sin[a], 1 > a > b > 0}, {a, b, CD}]

nyy

王守恩 发表于 2025-4-7 16:28
∠DAB=a。∠ABE=b。后面用的是正弦定理。 前面用的是角分线(不一定等分)定理。

Solve[{Sin Sin[Pi/6 + a]/ ...

要有注释有缩进，把代码放到代码框里面，
要有求解结果，把求解结果用latex表达（直接复制转化成）

hejoseph

如图，以 \(\overline{BC}\) 为正方向定义直线 \(BC\) 上的有向线段方向，\(BC=a\)，\(DE/AE=k\)，则
\begin{align*}
\overline{BE}&=\frac{2k\csc A\cos B\sin C-1-\sqrt{1+4k\csc A\sin B\sin C(\cot D-k\csc A\sin B\sin C)}}{2(k-1)}a\\
\overline{EC}&=\frac{2k\csc A\sin B\cos C-1+\sqrt{1+4k\csc A\sin B\sin C(\cot D-k\csc A\sin B\sin C)}}{2(k-1)}a\\
\end{align*}
（此时点 \(D\) 在直线 \(BC\) 上的正射影与点 \(C\) 在 \(BC\) 中点的同侧）
或
\begin{align*}
\overline{BE}&=\frac{2k\csc A\cos B\sin C-1+\sqrt{1+4k\csc A\sin B\sin C(\cot D-k\csc A\sin B\sin C)}}{2(k-1)}a\\
\overline{EC}&=\frac{2k\csc A\sin B\cos C-1-\sqrt{1+4k\csc A\sin B\sin C(\cot D-k\csc A\sin B\sin C)}}{2(k-1)}a\\
\end{align*}
（此时点 \(D\) 在直线 \(BC\) 上的正射影与点 \(B\) 在 \(BC\) 中点的同侧）

hejoseph

对于 \(\angle A=90^\circ\)，\(\angle B=30^\circ\)，\(\angle C=60^\circ\)，\(\angle D=60^\circ\)，\(k=3/2\)，代入楼上第一组式子就得
\[
\overline{BE}=\frac{5-\sqrt{13}}{4}a，\overline{EC}=\frac{-1+\sqrt{13}}{4}a，
\]
那么
\[
\overline{EC}=\frac{\dfrac{-1+\sqrt{13}}{4}a}{\dfrac{5-\sqrt{13}}{4}a}\times 4=\frac{8+4\sqrt{13}}{3}
\]