三角形内两两相切的圆

KeyTo9_Fans

给出三角形的三边长$a$、$b$、$c$。

在这个三角形内作三个圆。

要求每个圆都与其他两个圆以及三角形的两边相切。



1.如何根据$a$、$b$、$c$的值求出三个圆的半径$r_1$、$r_2$、$r_3$？

2.是不是$a=b=c$时三个圆的面积之和与三角形的面积之比最大？

此题来源于

http://bbs.emath.ac.cn/viewthread.php?tid=1494&fromuid=1394

第30题。（做了一些改动）

mathe

半径应该都可以用暴力计算出来的（特别有计算机帮忙 )

数学星空

如下图:


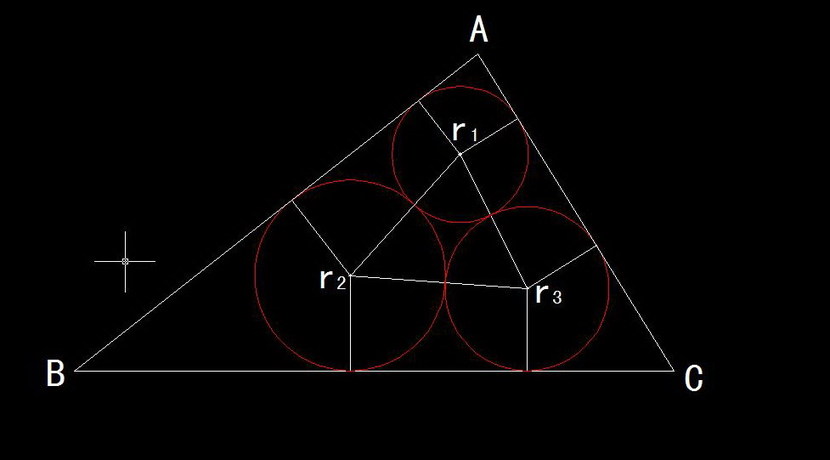设$x=ctg(A/2)=sqrt({(b+c-a)*(a+b+c)}/{(a+c-b)*(a+b-c)}}$
    $y=ctg(B/2)=sqrt({(a+c-b)*(a+b+c)}/{(b+a-c)*(b+c-a)}}$
     $z=ctg(C/2)=sqrt({(a+b-c)*(a+b+c)}/{(c+a-b)*(c+b-a)}}$
可以得到方程
  $ 4*r1*r2=(c-r1*x-r2*y)^2    .....(1)$      
    $4*r1*r3=(b-r1*x-r3*z)^2    .....(2)$      
     $4*r2*r3=(a-r2*y-r3*z)^2   .....(3)$
  我们可以利用数学软件求解(1),(2),(3)
  例如:我们消元可以得到关于r1的两个四次方程
      
($16*x^4*y^2*z^2-32*x^4*y*z-32*x^3*y^2*z-32*x^3*y*z^2-$$64*x^3*y*z+16*x^4+32*x^3*y+32*x^3*z+16*x^2*y^2+32*x^2*y*z+$
$16*x^2*z^2+64*x^3+64*x^2*y+64*x^2*z+64*x^2)*r1^4+$
$(-32*b*x^3*y^2*z^2+64*b*x^3*y*z+32*b*x^2*y^2*z+64*b*x^2*y*z^2+$
$32*c*x^3*y*z-32*c*x^2*y*z^2+96*b*x^2*y*z+64*c*x^2*y*z-32*b*x^3-$
$32*b*x^2*y-64*b*x^2*z-32*b*x*y*z-32*b*x*z^2-32*c*x^3-$$32*c*x^2*y+96*c*x*y*z+32*c*x*z^2-96*b*x^2-32*b*x*y-96*b*x*z-$
$128*c*x^2-64*c*x*y-64*b*x-192*c*x-64*c*y-64*c*z-128*c)*r1^3+$
$(24*b^2*x^2*y^2*z^2-40*b^2*x^2*y*z-8*b^2*x*y^2*z-40*b^2*x*y*z^2-$$64*b*c*x^2*y*z+32*b*c*x*y*z^2-16*b^2*x*y*z-$$128*b*c*x*y*z+16*b^2*x^2+16*b^2*x*y+48*b^2*x*z+16*b^2*y*z+$
$16*b^2*z^2+64*b*c*x^2+32*b*c*x*y-32*b*c*x*z-64*b*c*y*z-$$32*b*c*z^2+16*c^2*x^2+32*c^2*x*z+16*c^2*z^2+32*b^2*x+$
$32*b^2*z+160*b*c*x+64*b*c*y-32*b*c*z+64*c^2*x+64*c^2*z+$
$128*b*c+64*c^2)*r1^2+(-8*b^3*x*y^2*z^2+8*b^3*x*y*z+8*b^3*y*z^2+$
$40*b^2*c*x*y*z-8*b^2*c*y*z^2-8*b^3*y*z+48*b^2*c*y*z-16*b^3*z-$
$32*b^2*c*x-16*b^2*c*y+32*b^2*c*z-32*b*c^2*x-32*b*c^2*z-32*b^2*c-$
$64*b*c^2)*r1+(16*b^2*c^2-8*b^3*c*y*z+b^4*y^2*z^2)=0   $.....(A)


$(16*x^4*y^2*z^2-32*x^4*y*z-32*x^3*y^2*z-$$32*x^3*y*z^2+64*x^3*y*z+16*x^4+32*x^3*y+32*x^3*z+16*x^2*y^2+$
$32*x^2*y*z+16*x^2*z^2-64*x^3-64*x^2*y-64*x^2*z+64*x^2)*r1^4+$
$(-32*b*x^3*y^2*z^2+64*b*x^3*y*z+32*b*x^2*y^2*z+64*b*x^2*y*z^2+$
$32*c*x^3*y*z-32*c*x^2*y*z^2-96*b*x^2*y*z-64*c*x^2*y*z-32*b*x^3-$
$32*b*x^2*y-64*b*x^2*z-32*b*x*y*z-32*b*x*z^2-32*c*x^3-$$32*c*x^2*y+96*c*x*y*z+32*c*x*z^2+96*b*x^2+32*b*x*y+96*b*x*z+$
$128*c*x^2+64*c*x*y-64*b*x-192*c*x-64*c*y-64*c*z+128*c)*r1^3+$$(24*b^2*x^2*y^2*z^2-40*b^2*x^2*y*z-8*b^2*x*y^2*z-40*b^2*x*y*z^2-$$64*b*c*x^2*y*z+32*b*c*x*y*z^2+16*b^2*x*y*z+128*b*c*x*y*z+16*b^2*x^2+$
$16*b^2*x*y+48*b^2*x*z+16*b^2*y*z+16*b^2*z^2+64*b*c*x^2+32*b*c*x*y-$
$32*b*c*x*z-64*b*c*y*z-32*b*c*z^2+16*c^2*x^2+32*c^2*x*z+16*c^2*z^2-$
$32*b^2*x-32*b^2*z-160*b*c*x-64*b*c*y+32*b*c*z-64*c^2*x-64*c^2*z+$
$128*b*c+64*c^2)*r1^2+(-8*b^3*x*y^2*z^2+8*b^3*x*y*z+8*b^3*y*z^2+$
$40*b^2*c*x*y*z-8*b^2*c*y*z^2+8*b^3*y*z-48*b^2*c*y*z-16*b^3*z-$
$32*b^2*c*x-16*b^2*c*y+32*b^2*c*z-32*b*c^2*x-32*b*c^2*z+32*b^2*c+$
$64*b*c^2)*r1+(16*b^2*c^2-$
$8*b^3*c*y*z+b^4*y^2*z^2=0 $ ..........(B)
对于具体的三角形$a,b,c$,利用以上的方程也很容易算出$r1,r2,r3$

mathe

太复杂了。这个题目中我们如果用$r_1,r_2,r_3$来表示$a,b,c$以及两个三角形的面积会不会简单些？

kon3155

Although these circles were for many years thought to provide the solutions to Malfatti's problem, they were subsequently shown never to provide the solution.

http://mathworld.wolfram.com/MalfattiCircles.html

数学星空

楼上给出的链接,
是求解一个六元方程组,我利用MATHEMATICA 和MAPLE均无法正常运行,不知是用什么软件解出来f(a,b,c)的方程.....

northwolves

好复杂的问题

wiley

6# 数学星空

mathworld上给的是x的八次方程.  不过单墫<平面几何中的小花>里有给定一个三角形, 如何用尺规作图得到这三个圆的方法(J. Steiner 1826), 所以理论上应该可以用根式表达所有的半径和坐标.  不过我大概查了一下文献, 没有找到具体形式 (应该比楼主上次的那个几何问题还要繁).

数学星空

呵,我给出的是两个四次方程,即一个八次方程因式分解后得到了,所以我给出的(A),(B)应该没错,只是表达式太繁,
用数学软件都无法进一步化简了(即将(A),(B)转化为a,b,c的表达式)...

数学星空

尺规作图的作法见下图: