不等式专家的一个猜想

mathe

实际上是$k_n={2n(n-1)}/m-1$,其中$m=(n-u)u$,u为使得m取最大的整数，也就是最接近$n/2$的整数。
根据前面的分析我们可以知道，当让a无限逼近b的时候（也就$A=a/b->1$），这个$k_n$可以被无限逼近。
也就是$k_n$不得大于这个值。
然后我们需要证明对于这个$k_n$，不等式总是成立的，为此，我们可以记函数
$f(a)=(n-1)*(1-a)^2-(1+k_n*a)*(u*a+n-u-n*a^(u/n))$,也就是题目中b取1，然后左边u个数字取a,n-u个数字取1，其中($1<=u<=n-1$)然后通分
我们需要证明$f(a)>=0$,为方便起见，我们用k来代替$k_n$，然后输入maxima,并计算前3阶导数,
得到：

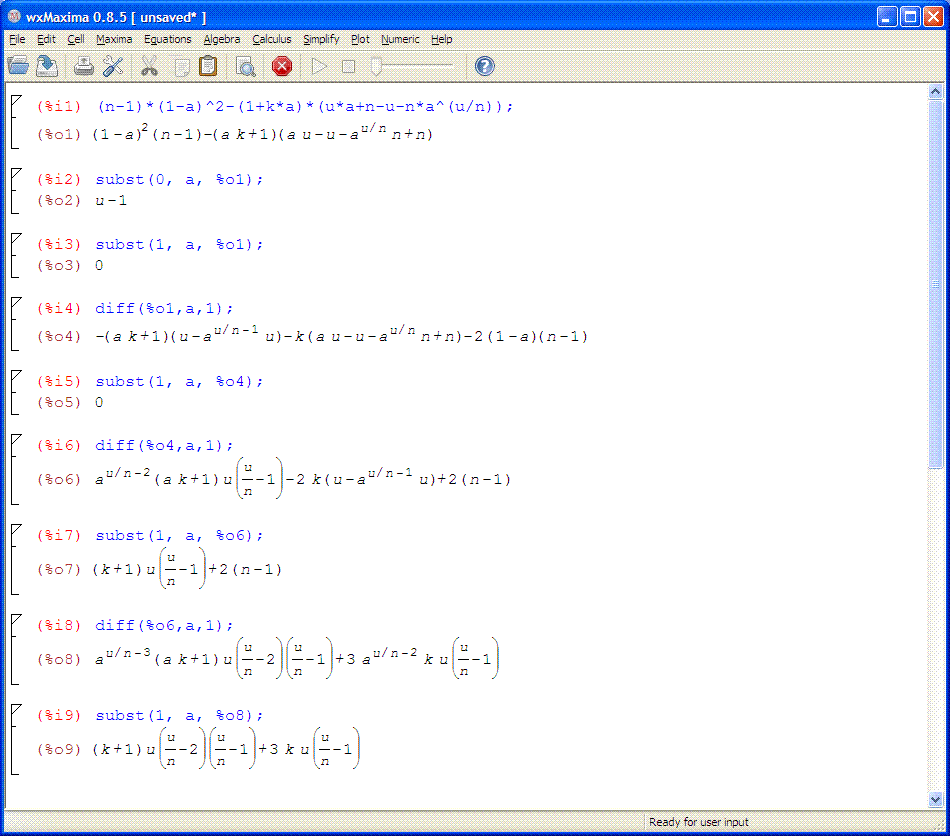其中
f(a)=%o1
f(0)=u-1>=0
f(1)=0
f'(a)=%o4
f'(1)=0
f'(0)=+infty
f''(a)=%o6
f''(0)=-infty
f''(1)=2(n-1)-(k+1)*u*(n-u)/n>=0,这里利用了$k_n$满足的不等式
f'''(a)=%o8
f'''(0)=+infty
f'''(1)<0
而且显然f'''(a)=0 在(0,1)有唯一解（提取公因子a^(u/n-3)后是a的线性函数）
所以f''(a)先增后减
得出f''(a)=0在(0,1)有唯一解
f'(a)先减后增
得出f'(a)=0在(0,1)有唯一解
得出f(a)先增后减
得出f(a)>=0,得证