如何將此圖形切成四份，再拼成一個正方形？

ejsoon

正方形上方缺三角形，餘下面積為原來的四分之三。

據說切成五塊是1920s有人發現了，之後他說不會有切成四塊的解決方案。

但是在2024年，有人找到了切成四塊的方法。

hujunhua

ejsoon

hujunhua 发表于 2025-4-30 14:12

你的發現足以載入史冊。

根據這篇文章，世界上發現五塊解法的只有五人，現在你是第六個。

ejsoon

http://puzzles.50webs.org/various_dissection.html

150.—DISSECTING A MITRE.
解剖一個斜角



The figure that is perplexing the carpenter in the illustration represents a mitre. It will be seen that its proportions are those of a square with one quarter removed. The puzzle is to cut it into five pieces that will fit together and form a perfect square. I show an attempt, published in America, to perform the feat in four pieces, based on what is known as the "step principle," but it is a fallacy.
插圖中讓木匠困惑的圖形代表一個斜角。可以看出，其比例是一個正方形去除四分之一後的形狀。這個謎題是將其切割成五塊，能夠拼湊成一個完美的正方形。我展示了一個在美國發表的嘗試，試圖以四塊完成這項任務，基於所謂的「階梯原理」，但這是一個錯誤。

ejsoon

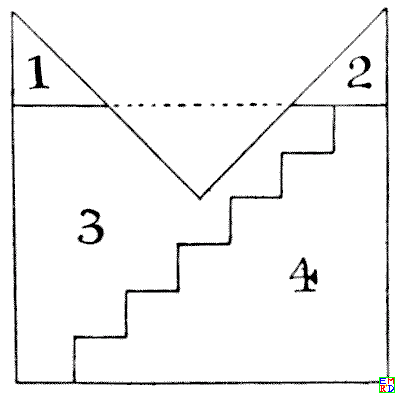
We are told first to cut oft the pieces 1 and 2 and pack them into the triangular space marked off by the dotted line, and so form a rectangle.

So far, so good. Now, we are directed to apply the old step principle, as shown, and, by moving down the piece 4 one step, form the required square. But, unfortunately, it does not produce a square: only an oblong. Call the three long sides of the mitre 84 in. each. Then, before cutting the steps, our rectangle in three pieces will be 84×63. The steps must be 10½ in. in height and 12 in. in breadth. Therefore, by moving down a step we reduce by 12 in. the side 84 in. and increase by 10½ in. the side 63 in. Hence our final rectangle must be 72 in. × 73½ in., which certainly is not a square! The fact is, the step principle can only be applied to rectangles with sides of particular relative lengths. For example, if the shorter side in this case were 615/7 (instead of 63), then the step method would apply. For the steps would then be 102/7 in. in height and 12 in. in breadth. Note that 615/7 × 84= the square of 72. At present no solution has been found in four pieces, and I do not believe one possible.

我們首先被告知要切下第1和第2塊，並將它們放入由虛線標記的三角形空間中，從而形成一個矩形。

到目前為止，一切順利。現在，我們被指示應用舊的階梯原理，如圖所示，通過將第4塊向下移動一階，形成所需的正方形。但不幸的是，這並未形成正方形：只形成了一個長方形。假設斜角的三個長邊各為84英寸。那麼，在切割階梯之前，我們的三塊矩形將為84×63英寸。階梯的高度必須為10½英寸，寬度為12英寸。因此，通過向下移動一階，我們將84英寸的邊減少12英寸，並將63英寸的邊增加10½英寸。因此，我們的最終矩形必須為72英寸×73½英寸，這顯然不是正方形！事實上，階梯原理僅適用於具有特定相對長度邊的矩形。例如，如果在這種情況下較短邊為615/7英寸（而不是63英寸），那麼階梯方法將適用。因為階梯的高度將為102/7英寸，寬度為12英寸。請注意，615/7 × 84 = 72的平方。目前尚未找到四塊的解決方案，我也不認為這是可能的。

ejsoon

DISSECTING A MITRE.—solution

The diagram on the next page shows how to cut into five pieces to form a square. The dotted lines are intended to show how to find the points C and F—the only difficulty. A B is half B D, and A E is parallel to B H. With the point of the compasses at B describe the arc H E, and A E will be the distance of C from B. Then F G equals B C less A B.

This puzzle—with the added condition that it shall be cut into four parts of the same size and shape—I have not been able to trace to an earlier date than 1835. Strictly speaking, it is, in that form, impossible of solution; but I give the answer that is always presented, and that seems to satisfy most people.



We are asked to assume that the two portions containing the same letter—AA, BB, CC, DD—are joined by "a mere hair," and are, therefore, only one piece. To the geometrician this is absurd, and the four shares are not equal in area unless they consist of two pieces each. If you make them equal in area, they will not be exactly alike in shape.



解剖一個斜角——解答

下一頁的圖表顯示了如何將其切割成五塊以形成一個正方形。虛線旨在展示如何找到C點和F點——這是唯一的難點。AB等於BD的一半，AE平行於BH。以B點為圓心，用圓規畫出弧HE，則AE將是C點到B點的距離。然後，FG等於BC減去AB。

這個謎題——加上必須切割成四個大小和形狀相同的部分的條件——我無法追溯到1835年之前。嚴格來說，在這種形式下，它是無法解決的；但我給出了通常呈現的答案，這似乎能滿足大多數人。

我們被要求假設包含相同字母的兩個部分——AA、BB、CC、DD——僅由「一根細毛」連接，因此只算作一塊。對幾何學家來說，這是荒謬的，除非每塊由兩部分組成，否則四塊的面積並不相等。如果讓它們面積相等，形狀就不會完全相同。

ejsoon

最終被我找到了，寡人表示非常開森！

https://vesatimonen.github.io/mitre-dissection/

ejsoon

ejsoon

前面的中文翻譯來自grok。

ejsoon

找到四塊切分方法的是一個芬蘭人，益智愛好者。他的工作是嵌入式工程師，他是用自己做的程式破解了這個謎題。