用Mathematica编程求出m使得误差函数值达到最小

笨笨

wayne

因为$\frac{\, _2F_1\left(-\frac{1}{2},-\frac{1}{2};1;\lambda ^2\right)}{\frac{3 \lambda ^2}{\sqrt{4-3 \lambda ^2}+10}+1}-1 = \frac{3 \lambda ^{10}}{131072}+\frac{67 \lambda ^{12}}{2097152}+O\left(\lambda ^{13}\right)$

而$\left(1-\frac{1-\lambda }{\lambda +1}\right)^{10} = 1024 \lambda ^{10}-10240 \lambda ^{11}+56320 \lambda ^{12}+O\left(\lambda ^{13}\right)$

所以里面的$\frac{22}{7 \pi }-1$应该换成$\frac{3}{134217728}$, 同时$m=10$
最终$\, _2F_1\left(-\frac{1}{2},-\frac{1}{2};1;\lambda ^2\right)-\left(\frac{3 \lambda ^2}{\sqrt{4-3 \lambda ^2}+10}+1\right) \left(\frac{3 \left(1-\frac{1-\lambda }{\lambda +1}\right)^{10}}{134217728}+1\right) =\frac{15 \lambda ^{11}}{65536}-\frac{2573 \lambda ^{12}}{2097152}+O\left(\lambda ^{13}\right)$

笨笨

wayne 发表于 2025-5-6 18:49
因为$\frac{\, _2F_1\left(-\frac{1}{2},-\frac{1}{2};1;\lambda ^2\right)}{\frac{3 \lambda ^2}{\sqrt{4- ...

前辈你好，你的解答不符合题意。

首先把\(\frac{22}{7 \pi }-1\)换成\(\frac{3}{134217728}\)且写成\(\left(1-\frac{1-\lambda }{\lambda +1}\right)^{10}\)这种形式求得的级数只能保证与原级数前几项高度相似，不能保证函数簇整体误差最小。



其次满足形如以下条件下的m值在误差函数簇中误差最小的那个。

wayne

我是觉得你的题目没出好,有点莫名其妙.所以擅自作主了.
既然你这么坚持,那请你严格定义一下 你新造的词汇,误差函数簇 的数学意义.

笨笨

wayne 发表于 2025-5-6 21:53
我是觉得你的题目没出好,有点莫名其妙.所以擅自作主了.
既然你这么坚持,那请你严格定义一下 你新造的词汇, ...

前辈你好，由于我没表达好且能力有限。主贴大致类似于这个帖子:用Mathematica编程求出最大误差函数值时如：10⁻⁸下的(x,a,b,c,d)
https://bbs.emath.ac.cn/forum.php?mod=viewthread&tid=18985
(出处: 数学研发论坛)

笨笨

@Ickiverar

笨笨

wayne 发表于 2025-5-6 21:53
我是觉得你的题目没出好,有点莫名其妙.所以擅自作主了.
既然你这么坚持,那请你严格定义一下 你新造的词汇, ...

大致就是这个意思，前辈请看下图

笨笨

折腾了2天未果！下面的程序deepseek算的结果很接近主贴所求m值。

最优参数 m = 46.4295，误差=0.00001868207537802924，b=0.05376700730325596

检验误差：

1. NumberForm[
   
2. N[NMaximize[{Abs[
   
3.      Hypergeometric2F1[-(1/2), -(1/2),
   
4.        1, ((1 - b)/(
   
5.         1 + b))^2] - (1 + (3 ((1 - b)/(1 + b))^2)/(
   
6.          10 + Sqrt[
   
7.           4 - 3 ((1 - b)/(1 + b))^2])) (1 + (22/(7 \[Pi]) - 1) (1 -
   
8.             b)^  46.42947629474779` )], 0 < b < 1}, b]], 10]

复制代码

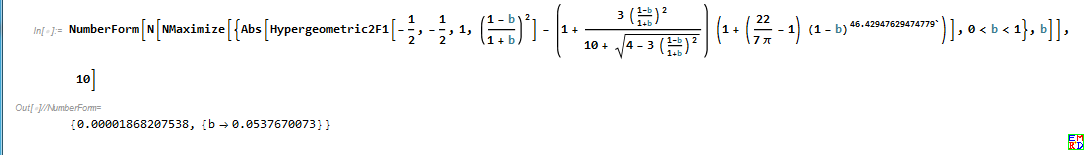
求出最优m值

1. (*左边 Hypergeometric 函数*)
   
2. left[x_] := Hypergeometric2F1[-1/2, -1/2, 1, ((1 - x)/(1 + x))^2];
   
3. 
   
4. (*右边修正后的表达式*)
   
5. right[x_,
   
6.    m_] := (1 + (3*((1 - x)/(1 + x))^2)/(10 +
   
7.         Sqrt[4 - 3*((1 - x)/(1 + x))^2]))*(1 + (22/(7*Pi) -
   
8.         1)*(1 - x)^m);
   
9. 
   
10. (*预计算常数项优化计算效率*)
    
11. constantFactor = N[22/(7*Pi) - 1];(* \[TildeTilde]-0.31831*)
    
12. right[x_?NumericQ,
    
13.   m_?NumericQ] := (1 + (3*((1 - x)/(1 + x))^2)/(10 +
    
14.        Sqrt[4 - 3*((1 - x)/(1 + x))^2]))*(1 +
    
15.     constantFactor*(1 - x)^m);
    
16. 
    
17. (*定义均方误差，积分区间设为[0,1]*)
    
18. mse[m_?NumericQ] :=
    
19.   NIntegrate[(left[x] - right[x, m])^2, {x, 0, 1},
    
20.    Method -> "GlobalAdaptive", MaxRecursion -> 20];
    
21. (*全局优化，限制 m>0*)
    
22. result = NMinimize[{mse[m], m > 0}, m, Method -> "SimulatedAnnealing"];
    
23. {minError, {mOpt -> mValue}} = result;
    
24. 
    
25. (*输出结果*)
    
26. Print["最优参数 m = ", mOpt, "，最小均方误差 = ", minError]
    
27. (*绘制函数对比*)optM = mOpt /. result[[2]];
    
28. Plot[{left[x], right[x, optM]}, {x, 0, 1},
    
29. PlotLegends -> {"Hypergeometric", "Approximation"},
    
30. PlotStyle -> {Blue, Red}, Frame -> True,
    
31. FrameLabel -> {"x", "Function Value"},
    
32. PlotLabel -> "Optimal m = " <> ToString[optM]]

复制代码

笨笨

固定椭圆长半轴a=1，用肉眼观察法可知主贴所求的m值在46.401附近使误差达到最小

1. Manipulate[
   
2. Plot[{Hypergeometric2F1[-(1/2), -(1/2),
   
3.      1, ((1 - b)/(
   
4.       1 + b))^2] - (1 + (3 ((1 - b)/(1 + b))^2)/(
   
5.        10 + Sqrt[
   
6.         4 - 3 ((1 - b)/(1 + b))^2])) (1 + (22/(7 \[Pi]) - 1) ((1 - b)/
   
7.          1)^m), -0.00002, 0.00002}, {b, 0, 1},
   
8.   PlotRange -> {-0.00002, 0.00002},
   
9.   Epilog -> {Dashed, Line[{{1, 0}, {1, -0.00002}, {1, 0.00002}}]},
   
10.   PlotLegends -> "Expressions"], {m, 0, 50}]

复制代码

笨笨

不知道8楼的代码怎么优化才能得到：m=46.401