搭桥(4)

KeyTo9_Fans

有一条无限长的河，宽度为$N$。 下图是宽度为$4$的河。红色表示河岸。 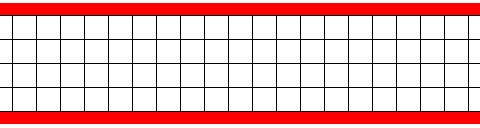有一个人想搭桥过河，有一个人想捣乱。 搭桥者每次可以在河里放一块$1xx1$的木板，捣乱者则可以在河里放一块$1xx1$的障碍。 木板不能放在障碍上，障碍也不能放在木板上。 搭桥者的木板是$4$连通的（往上下左右$4$个方向相连）。 如果搭桥者的木板把两岸连起来了（路线长度与拐弯数不限），则视为搭桥成功。 搭桥者和捣乱者身上都有$100$块钱。 他们每次都会同时开出一个价。 搭桥者的开价记为$a$，捣乱者的开价记为$b$。 如果$a>b$，则搭桥者付给捣乱者$a$块钱，然后在河里放一块木板。 如果$a<=b$，则捣乱者付给搭桥者$b$块钱，然后在河里放一块障碍。 开价不能高于自己当前拥有的钱数。 对于$N=1,2,3,4,...$，问： $1.$搭桥者是否有必胜策略？ $2.$无论搭桥者放$1$块木板还是捣乱者放$1$块障碍都视为$1$步。假设搭桥者想用尽可能少的步数把桥搭成，捣乱者则想尽可能多地增加步数。问搭桥成功所需步数的期望值$S(N)$是多少？ $3.$假设搭桥者一定要把桥搭成，但是想尽可能地省钱。而捣乱者则想尽可能多地赚钱。问搭桥成功后，搭桥者所剩钱数的期望值$V(N)$。

zeroieme

放板有限制么？是否除了不能放在障碍上，可随意放？包括没连接岸上，直接扔水面。

songdeng123

2# zeroieme 直接扔水里，不就被水冲走了啊？ 呵呵

gxqcn

应该假定水面为静止的（如果流速够快的快的话，无论是什么都给冲走了）。 还有，放木板或障碍的位置与人当前位置之间是否可跳空？或别的要求？

KeyTo9_Fans

水是静止的。 除了不能重叠，没有别的要求。 先讨论$N=1$的情况。