6 阶模幻方的搜索

hujunhua

$Z_6^2$上的最优幻方

        在编排6阶全对称幻方时，排成蜂窝状网格（又称为等距网格）比排成方格可体现更高的对称性，如图1所示。图中坐标相同的格为同一格，表现了所谓全对称幻方是嵌入到一个三维环面（轮胎面）的。在平面上表现时，可以按这个局部呈现的相邻关系扩展到整个平面上。扩展后，将视野取为一个如图2那样的正六角形区域时，呈现了6阶幻方的旋转对称性。在等距格网上，原来方格网上的一条对角线（x=y）看起来成为一条主轴。等距网格的对角线定义为相距次近的两格的连线，如图1中的黄色格列（在图2的正六角形视野中，呈现为正六角形的长对角线方向）。按此定义，6阶幻方有3条主轴方向和3条对角线方向，我们要求在其中的每一个方向上直线排列的6格数之和都等于幻方和数。这就比通常所谓的“全对称幻方”约束更多，对称性更高。

      

四边形视野

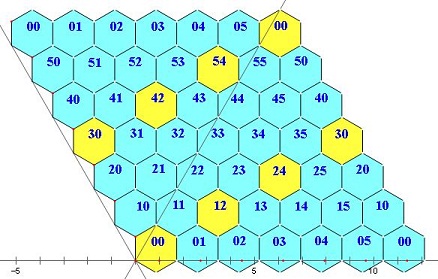
六角形视野

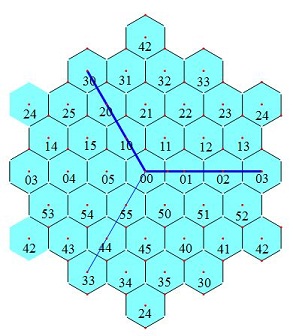
                               图1   菱形视野                                                                                                                                           图2 六角形视野
         用代数学的语言来描述，6阶幻方就是$Z_6^2$→｛1, 2, 3, ..., 36｝的一个映射f, f 满足某些函数方程，即幻方编排者所称的幻方律。比如关于行的幻方律即
               $ f(x,y)+f(x,y+1)+f(x,y+2)+...+f(x,y+5)=6A$($A$是36个填入数的平均值）
由于 f 的定义域为模$Z_6^2$, 所以这类幻方宜可称之为模上的幻方，简称模幻方。

       除了定义时给出的2条幻方律（其实是6条，但是可用主轴线和对角线分别概括），6阶模幻方还有一些导出的幻方律，展现了其6阶旋转对称性。

导出律1：对角线上的相间三格之和等于3A。如图3所示。变换视野，一条对角线的相间3格布成一个正三角形。图4显示两条这样的半对角线布成了一个正六角形，六角之和等于6A（导出律2）。
导出律3：见图5，4个黄色格（其中格33带红色纹线）之和等于4A。格33也可以在带纹线的青色格的位置，在此视野中这四格呈菱形。

幻方律1

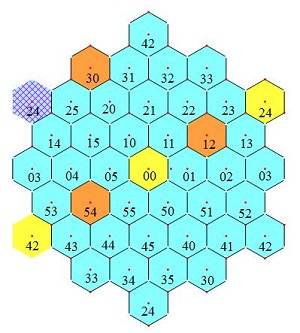
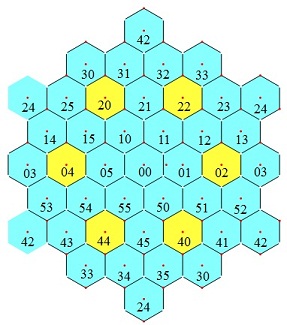
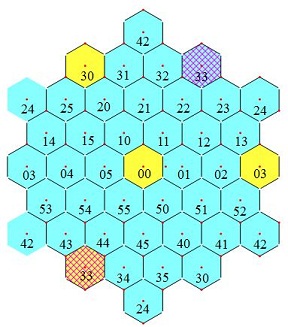
图3    导出律1：对角线上的相间三格之和等于3A                   图4  导出律2：正六角形的六角之和等于6A              图5 导出律3：边长为4格的菱形四角之和等于4A
      
        还有更多的表现6阶旋转对称性的导出律，下帖给出。这些导出律并非观察具体的数字而来，而是依据定义所给的约束方程消元而得。要用具体的数字来验证这些幻方律，我暂时还没有实例，因为我至今也没有编排出一个6阶模幻方的实例。事实上，对于这样的6阶幻方，用｛1, 2, 3, ..., 36｝是填不成功的。因为，图5中的4格减去图3中3格=4A-3A=A，所以A必须是整数。若用｛1, 2, 3, ..., 36｝，总和Σ=18×37，A=Σ/36 非整数。
        为了编出6阶模幻方，f 只能取其它的值域。为了保持幻方的数字之美，值域应该满足一定的要求。我们的要求是尽可能接近自然数前段{1~36}。由于18×37≡18(mod 36), 所以要使A为整数，最接近｛1~36｝的数组是从中去掉18，添上0，即｛0~17，19~36｝。

这就是本擂的目标：用｛0~17，19~36｝填入构建6阶模幻方。

hujunhua

导出律4：如图6所示的边平行于主轴的最小正六角形（黄色格），六角之和加上中心格的2倍等于8A
导出律5：如图7所示的边平行于对角线的最小正六角形（黄色格），六角之和减去中心格等于5A

图6 导出律4

图7 导出律5

         图6  导出律4                                                                            图7  导出律5

hujunhua

导出律6：图8所示正六角形区域的13个黄格之和等于13A. 由图6与图7叠加即得。 导出律7：图9所示正六边形区域的19个黄格之和等于19A. 由图8与图4叠加即得。

图8 导出律6

图9 导出律7

图8 导出律6 图9 导出律7

郭先抢

导出律6：图8所示正六角形区域的13个黄格之和等于13A. 由图6与图7叠加即得。 导出律7：图9所示正六边形区域的19个黄格之和等于19A. 由图8与图4叠加即得。 43554356 图8 导出律6 ... hujunhua 发表于 2013-1-6 11:35

我更关心你的图是如何弄出来的

hujunhua

4# 郭先抢 我会有交代的。 导出律1和导出律3涉及的格子少，导出律4涉及的格子密集，这很有利于手工得出参数解。图10就是一个在36个填入数之和为零（称为零和幻方）的条件下的参数布置方案。如果我们用填入数｛±1, ±2, ±3, ..., ±18｝,就会产生零和幻方。

图10 参数解

图10 参数解 6阶零和模幻方的定义中给出的36个约束方程的秩为24，所以参数解的维数为12. 上图中我们选两个白六角形的六个角a1,b1,...,f1, a2,b2, ..., f2为参数，其它格就可以由上述导出律得到。s1=-(a1+b1+...+f1)/2, s2=-(a2+b2+...+f2)/2, s3=-(s1+s2), a3=-(a1+a2),....

mathematica

为什么不是精华帖呢?

hujunhua

终于自己编了程序开始搜索，已经计算20个小时了，还没有输出一个结果， 也就是说搜索到现在还没有发现一个解。
都快失去信心了，担心会最后运行结果就是这样无息而终。那就表明问题是无解的，或者程序有问题。
很后悔没有输出一些中间结果来提示进度，现在没法估计还得多久搜索计算完。

@wayne @chyanog现在能否将程序暂停，以便通过查看中间结果了解进度，然后再继续？

wayne

hujunhua 发表于 2015-7-5 00:44
终于自己编了程序开始搜索，已经计算20个小时了，还没有输出一个结果， 也就是说搜索到现在还没有发现一个 ...

程序正在运行的时候，查看中间结果，这个我没有做过。
====
可以再QQ群里@chyanog

hujunhua

今天上午9点将程序终止运行了，检查中间结果，发现进度大约为5%。程序运行了52小时。
照此速度，全部搜索完得1000小时。太恐怖了！当初阿佩尔证明四色定理也才计算了1200小时。

chyanog

我们要求在其中的每一个方向上直线排列的6格数之和都等于幻方和数

这句话怎么理解？