一维空间中的吃豆子问题

KeyTo9_Fans

实验表明，当$k=2$时，“总是吃最近的豆子”并不是最佳策略。 当两个豆子差不多近时，优先吃边上的豆子，可以吃得更快 具体的策略函数如下： 如果Score$(x_1)>$Score$(x_2)$，那么$f(x_1,x_2,x_w)=Go(x_w->x_1)$，否则$f(x_1,x_2,x_w)=Go(x_w->x_2)$。 其中： $Sco re(x_i)={|x_i-1/2|+1/2}/{|x_w-x_i|}$，（表示豆子离$1/2$处越远越好，离wayne越近越好） $Go(x_w->x_i)$表示$x_i$在$x_w$的哪边就去哪边。 该策略吃豆子的平均速率是$(4.55648\pm0.00001)$个每秒，比“总是吃最近的豆子”的策略好。 （$3$楼“总是吃最近的豆子”的策略的速率只有$(4.53704\pm0.00002)$个每秒）

wayne

11# KeyTo9_Fans “总是吃最近的豆子” 是局部最优，全局最优的话，需要时时刻刻以当前自身的位置作为距离计算的参照点，作为评估函数。 fans给的这个score很靠谱。但有一个1/2在里面，不是很和谐啊。

mathe

k=2时Fans可以试着给个离散解看看？ 其实k=2时，本质是求一个函数$g(x_1,x_2)$,如果$x_wg(x_1,x_2)$选择右边。同样k=n时是求一个将n个数映射到n-1个数的函数。 而给定选择函数，应该可以通过迭代得出$(x_1,x_2,...,x_k,x_w)$的一个稳定的分布密度，也就是经过一次迭代后密度函数保持不变。然后计算这个密度函数下的平均速率，所以是一个带额外约束条件变分问题，只是k越大，表达式越复杂，很难计算。

zgg___

对于两个点的情况，如13层所说，尝试了一些函数g，最后还是选择了平均数，令gq(x1,x2)为x1、x2和1/2这三个数的加权算数平均数，其权的比例为1：1：q，故gq(x1,x2)=(x1+x2+q/2)/(q+2)。然后做了一点数据模拟，对每一个k，每次吃10^5个豆，反复吃50次求平均、最大和最小（代码见下）。

1. g[x1_, x2_, k_] := (x1 + x2 + k/2)/(k + 2);
2. ks = {};
3. Do[ts = {};
4. Do[w = 0.5; t = 0; s1 = Random[]; s2 = Random[];
5. Do[If[s1 < s2, x1 = s1; x2 = s2, x1 = s2; x2 = s1;];
6. If[w < g[x1, x2, k], tt = Abs[w - x1]; w = x1; s1 = x2;,
7. tt = Abs[w - x2]; w = x2; s1 = x1;];
8. s2 = Random[]; t = (t n + tt)/(n + 1);, {n, 0, 100000}];
9. AppendTo[ts, t];, {50}];
10. AppendTo[ks, {{k, Mean[ts]}, {k, Min[ts]}, {k, Max[ts]}}];
11. Print[k];, {k, 0, 2, 0.1}];
12. ListPlot[Transpose[ks], Filling -> {1 -> {2}, 1 -> {3}},
13. PlotMarkers -> {" \[FilledCircle]", "\[LongDash]", "\[LongDash]"}]

复制代码

结果如图，纵轴是吃每一个豆的平均时长，是lz说的吃豆速度的倒数，横轴是1/2的权重，当权重q=0，相当于吃最近的，当权重q很大时，相当于随便吃，即每次出现一个豆的情况(k=1)。此代码效率低，有空弄个好点的。

wayne

14# zgg___ nice. 不过，我比较关注的是，这个图像稳定吗

zgg___

14L的图是反复吃50次求平均、最大和最小的结果（分别对应图中的点和上下边），看到长长的竖线，图形当然是不稳定的了，呵呵。不过总趋势是稳定的，所以要用c再弄一个验证下。呵呵。

wayne

16# zgg___ 像fans问的这种题，我的直觉是，我们排除不了那种类似于混沌分形的非线性格局的可能性(例如遍历假说)。

zgg___

算了一下10^7个豆的，吃10次，结果比较好看了。

zgg___

又弄了一个10^8的豆的，感觉上需要验证随机数的可靠性和考虑double的误差积累了。所以请Fans也有空算一下权重p的极小值吧。呵呵。 源码如下，我用vc2005：

1. #include "stdafx.h"
2. #include <conio.h>
3. #include <stdlib.h>
4. #include <time.h>
5. typedef double F;
6. int _tmain(int argc, _TCHAR* argv[])
7. {
8. FILE *fp;
9. long i,j,n;
10. F w,t,s1,s2,k,x1,x2;
11. srand((unsigned)time(NULL));
12. fopen_s(&fp,"d:\\chidou.txt","w");fprintf(fp,"s={");
13. n=100000000L;
14. for(k=0.0;k<2.01;k+=0.1){
15. for(j=0;j<10L;j++){
16. w=0.5;t=0.0;s1=(F)rand()/RAND_MAX;
17. for(i=0;i<n;i++){s2=(F)rand()/RAND_MAX;
18. if(s1<s2){x1=s1;x1=s1;x2=s2;}else{x1=s2;x2=s1;}
19. if(w<(x1+x2+k/2.0)/(k+2.0)){t+=(w>x1)?w-x1:x1-w;w=x1;s1=x2;}else{t+=(w>x2)?w-x2:x2-w;w=x2;s1=x1;}}
20. printf("j=%3d; k=%f; t=%f\n",j,k,t/n);fprintf(fp,"%f,",t/n);}}fprintf(fp,"0};");
21. return 0;
22. }

复制代码

M画图代码：

1. <<"d:\\chidou.txt"
2. ss=Transpose[Map[{Mean[#],Max[#],Min[#]}&,Partition[Most[s],{10}]]];ss//First
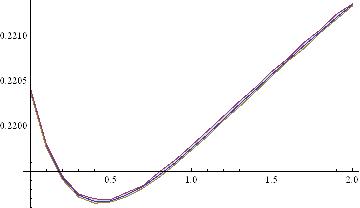
3. ListPlot[Map[Transpose[{Range[0,2,1/10],#}]&,ss],Filling->{1->{2},1->{3}},Joined->True]

复制代码

结果如下，权重p为0到2，0.1步长，结果是吃豆的期望时长： {0.220413,0.219784,0.219428,0.219236,0.219167,0.219171,0.21924,0.219331,0.219458,0.219596,0.219753,0.219908,0.220075,0.220245,0.220406,0.220575,0.220731,0.220894,0.221046,0.221204,0.221347}

wayne

17# wayne 用大数定理，好像可以直接否掉我的直觉，汗...