一道平面几何

葛雨润 · 发表于 2013-3-2 21:46:18

马上注册，结交更多好友，享用更多功能，让你轻松玩转社区。

您需要登录才可以下载或查看，没有账号？欢迎注册

×

已知三角形ABC中，∠BCA=90°，D是过顶点C的高的垂足，设X是线段CD内部一点，K是线段AX上一点，使得BK=BC，L是BX上一点，使得AL=AC，设M是AL与BK的交点，求证MK=ML

wayne · 发表于 2013-3-7 12:02:01

给楼主配一个图

hujunhua · 发表于 2013-3-7 23:05:42

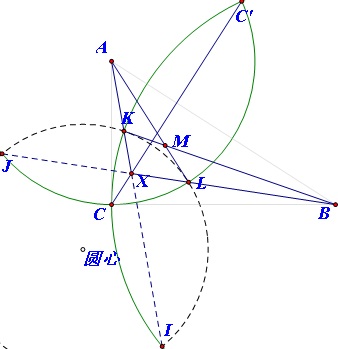
证明：作出以三角形的直角边为半径的圆A和圆B，两圆相交于直角顶点C及C关于斜边AB的镜像点C'. 于是题目可以重新描述如下：已知：圆A和圆B正交于点C和C‘，X是两圆公共弦CC'上的点，线段AX交圆B于K，线段BX交圆A于L, .......... 下面来完成证明。作出直线AX、BX各与圆B、圆A的另一交点I、J; 由相交弦定理得KX·XI=CX·XC'=LX·XJ, 故IJKL四点共圆。圆A与圆B正交→{J,L}为基于圆B的反演共轭点对→圆B与圆IJKL正交→BK为圆IJKL的切线同理可得圆A与圆IJKL正交，AL亦为圆IJKL的切线。故MK=ML. 几何难题征解1.jpg

gxqcn · 发表于 2013-3-8 08:24:29

巧用圆的性质，漂亮！

账号		自动登录	找回密码
密码			欢迎注册

[提问] 一道平面几何

马上注册，结交更多好友，享用更多功能，让你轻松玩转社区。

评分

评分