数字"1"在三角阵中的生存概率

wayne · 发表于 2013-8-1 21:28:02

把上面的关于p的多项式 (生存概率) 画在一个图里面，看看趋势：
貌似N 越大，曲线的坡度越陡，越接近于一个阶跃函数(90度的折线)。

mathe · 发表于 2013-8-1 22:12:32

越阶处即分界线。你能算出1的期望数目关于p的多项式吗

wayne · 发表于 2013-8-1 22:31:35

mathe 发表于 2013-8-1 22:12
越阶处即分界线。你能算出1的期望数目关于p的多项式吗

如mathe所言，给出1的期望数目

{4,2 p}
{5,-(-4+p) p^2}
{6,-4 (-2+p) p^3}
{7,p^4 (16-12 p+p^2-p^3+p^4)}
{8,-2 p^5 (4-3 p-p^2+p^3) (-4+p-p^2+p^3)}
{9,p^6 (64-80 p+24 p^2-13 p^3+6 p^4+8 p^5+8 p^6-14 p^7+4 p^8)}
{10,-2 p^7 (-64+96 p-40 p^2+20 p^3-10 p^4-8 p^5-7 p^6-4 p^7+28 p^8-18 p^9+3 p^10)}
{11,p^8 (256-448 p+240 p^2-120 p^3+65 p^4+29 p^5+24 p^6+5 p^7+14 p^8-204 p^9+223 p^10-97 p^11+31 p^12-10 p^13+p^14)}
{12,-2 p^9 (-256+512 p-336 p^2+176 p^3-101 p^4-20 p^5-20 p^6+6 p^7-7 p^8-12 p^9+343 p^10-524 p^11+330 p^12-122 p^13+p^14+48 p^15-27 p^16+4 p^17)}
{13,-p^10 (-1024+2304 p-1792 p^2+1008 p^3-604 p^4-7 p^5-68 p^6+69 p^7-12 p^8-15 p^9-166 p^10+2604 p^11-4980 p^12+4341 p^13-2562 p^14+1088 p^15-364 p^16+609 p^17-718 p^18+335 p^19-66 p^20+14 p^21-6 p^22+p^23)}
{14,-2 p^11 (-1024+2560 p-2304 p^2+1408 p^3-876 p^4+118 p^5-68 p^6+116 p^7-9 p^8+10 p^9-176 p^10-4 p^11+4438 p^12-10544 p^13+11162 p^14-7556 p^15+3042 p^16+510 p^17-1475 p^18+2100 p^19-3196 p^20+2676 p^21-1190 p^22+388 p^23-142 p^24+20 p^25+17 p^26-8 p^27+p^28)}
{15,-p^12 (-4096+11264 p-11520 p^2+7680 p^3-4960 p^4+1252 p^5-369 p^6+669 p^7-83 p^8+120 p^9-802 p^10+237 p^11-1050 p^12+34193 p^13-94583 p^14+121472 p^15-103735 p^16+66516 p^17-31313 p^18+23392 p^19-31180 p^20+39705 p^21-56551 p^22+62657 p^23-43426 p^24+20198 p^25-7060 p^26+585 p^27+1347 p^28-474 p^29-272 p^30+226 p^31-57 p^32+5 p^33)}

复制代码

再给一下图像：

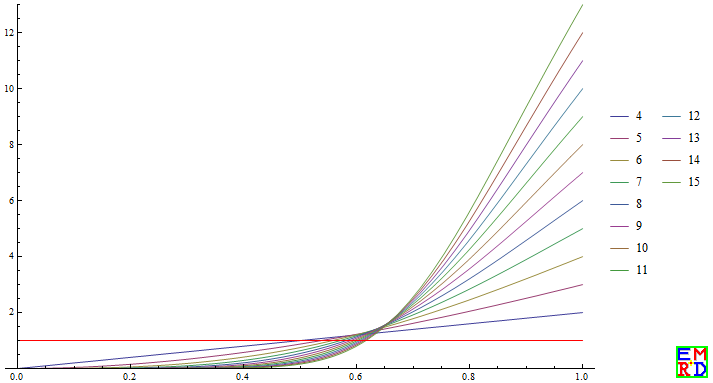
然后计算这些1的期望数目的多项式=1的时候p的值：
{4,0.5000000000}
{5,0.5374015770}
{6,0.5575439973}
{7,0.5712360524}
{8,0.5813885621}
{9,0.5893377588}
{10,0.5957991736}
{11,0.6011967994}
{12,0.6058008376}
{13,0.6097931583}
{14,0.6133015047}
{15,0.6164187214}

附带给出代码：

t={{{0,1,0},1}};
d=Table[{n+3,t=Table[{g[[1,1]],Total[g[[All,2]]]//Factor},{g,GatherBy[Flatten[Table[Table[{{0,Sequence@@k[[All,1]],0},(k[[All,2]]/.List->Times)i[[2]]},{k,Tuples[Table[If[i[[1,ii]]+i[[1,ii+1]]==0,{{0,1}},{{0,(1-p)},{1,p}}],{ii,Length[i[[1]]]-1}]]}],{i,t}],1],#[[1]]&]}];
Factor@Sum[Total[i[[1]]]*i[[2]], {i, t}]},{n,8}]

复制代码

KeyTo9_Fans · 发表于 2018-2-3 03:33:34

我把楼主的问题做成了一个游戏。

下载这个附件，解压后就可以玩这个游戏了：

01Triangle.zip (84.92 KB, 下载次数: 3)

玩法简介：

用键盘输入$p$的值，然后按回车键，就可以看到数字$1$在三角阵中如何生存了（数字$1$用黑色方块表示），如下图所示：

如果想移动显示的区域，按方向键或翻页键即可，最多显示到第$10000$行，这$1$万行数据一共占用$6$MB的内存。

随机数用time(NULL)种子、rand()函数和噪声生成，周期约为$10^14$，大概够玩$100$万次。

#####

玩了多次之后可以发现数字$1$能否生生不息的分界点在$p=0.7$附近。

wayne · 发表于 2018-2-3 09:19:31

好感动，五年前的帖子。留下的还在活跃的都是真爱呀，

KeyTo9_Fans · 发表于 2018-2-3 12:04:43

是呀~ 那个时候《数学研发论坛》刚从5d6d里迁出不久，这是我在论坛迁移后发的第$1$个主题，被系统识别成【新人贴】了

#####

问题$1$：当$p=0.75$时，数字$1$的生存概率是多少？

我们一行一行来分析。

新增$1$行：$0.0625$几率死掉，$0.375$几率存活$1$个，$0.5625$几率存活$2$个。

新增$2$行：$0.0947265625$几率死掉，$0.2197265625$几率存活$1$个，$0.4482421875$几率存活$2$个，$0.2373046875$几率存活$3$个。

此时，存活$2$个有两种情况：并排的$11$和隔空的$101$。

由于隔空的$101$与存活$3$个是等效的，应归并到存活$3$个的情况里，归并之后的结果如下：

新增$2$行：$0.0947265625$几率死掉，$0.2197265625$几率存活$1$个，$0.369140625$存活$2$个，$0.31640625$几率存活$3$个。

新增$3$行：$0.1154632568359375$几率死掉，存活状态有$5$种：$1, 11, 111, 1001, 1111$，手算几率比较麻烦，暂时不算了。

新增$4$行：新增$4$种存活状态：$10001, 10011, 11001, 11111$。

新增$5$行：新增$7$种存活状态：$100001, 100011, 110001, 100111, 111001, 110011, 111111$。

新增$6$行：新增$12$种存活状态：$1000001, 1000011, 1001001, 1100001, 1000111, 1110001, 1100011, 1001111, 1111001, 1100111, 1110011, 1111111$。

新增$7$行：新增$21$种存活状态：略。

新增$8$行：新增$37$种存活状态：略。

新增$9$行：新增$65$种存活状态：略。

……

记新增的状态数为$a(n)$，则有$a(n) = a(n-1) + a(n-2) + a(n-4)$，该数列被收录在A005251。

#####

由于状态数增长得太快了，即使合并了左右对称的状态之后，状态数依然呈指数级增长，因此难以逐一计算几率。

于是把$p$的值设为$0.75$，然后直接玩$1$亿次游戏，然后统计这$1$亿次游戏中，数字$1$死在新增的第$n$行的次数，结果如下：

1: 6249297
2: 3223650
3: 2075642
4: 1476786
5: 1116333
6: 880046
7: 708667
8: 586003
9: 493423
10: 421340
11: 360387
12: 314441
13: 275779
14: 242733
15: 215845
16: 192579
17: 171848
18: 154209
19: 139657
20: 126890
21: 115322
22: 105784
23: 95462
24: 87696
25: 80460
26: 74757
27: 68186
28: 62607
29: 58135
30: 54372
31: 50723
32: 46610
33: 43224
34: 40741
35: 37307
36: 35261
37: 32360
38: 30417
39: 28410
40: 26921
41: 25097
42: 23889
43: 22359
44: 20996
45: 19582
46: 18653
47: 17321
48: 16469
49: 15380
50: 14371
51: 14018
52: 13065
53: 12265
54: 11544
55: 10767
56: 10301
57: 9747
58: 9274
59: 8641
60: 8302
61: 7919
62: 7402
63: 7007
64: 6754
65: 6261
66: 5978
67: 5604
68: 5449
69: 5179
70: 4966
71: 4627
72: 4463
73: 4244
74: 4031
75: 3865
76: 3664
77: 3491
78: 3234
79: 3262
80: 3040
81: 2970
82: 2709
83: 2678
84: 2523
85: 2466
86: 2192
87: 2206
88: 2040
89: 1971
90: 1934
91: 1758
92: 1716
93: 1631
94: 1594
95: 1560
96: 1446
97: 1334
98: 1335
99: 1291

复制代码

而新增$100$行都没死的次数是$78959855$。

由于新增$100$行后，再继续模拟下去效率太低了，

因此不再往下模拟，而是根据以上数据的走势预测后续数据，结果如下：

100: 1239
101: 1188
102: 1139
103: 1092
104: 1048
105: 1005
106: 965
107: 925
108: 889
109: 853
110: 819
111: 786
112: 756
113: 725
114: 698
115: 670
116: 644
117: 619
118: 595
119: 573
120: 550
121: 530
122: 509
123: 491
124: 471
125: 454
126: 437
127: 421
128: 405
129: 390
130: 376
131: 361
132: 349
133: 336
134: 323
135: 312
136: 301
137: 290
138: 279
139: 269
140: 260
141: 251
142: 241
143: 233
144: 225
145: 217
146: 210
147: 202
148: 195
149: 188
150: 182
151: 175
152: 170
153: 163
154: 158
155: 153
156: 147
157: 143
158: 137
159: 133
160: 129
161: 124
162: 120
163: 116
164: 112
165: 109
166: 105
167: 101
168: 98
169: 95
170: 92
171: 89
172: 86
173: 83
174: 80
175: 78
176: 75
177: 73
178: 71
179: 68
180: 66
181: 64
182: 62
183: 60
184: 59
185: 56
186: 54
187: 53
188: 51
189: 50
190: 48
191: 47
192: 45
193: 43
194: 43
195: 41
196: 40
197: 38
198: 38
199: 36
200: 35
201: 34
202: 33
203: 32
204: 31
205: 30
206: 30
207: 28
208: 28
209: 26
210: 26
211: 25
212: 25
213: 23
214: 23
215: 23
216: 21
217: 21
218: 21
219: 20
220: 19
221: 18
222: 19
223: 17
224: 17
225: 17
226: 16
227: 16
228: 15
229: 15
230: 14
231: 14
232: 13
233: 13
234: 13
235: 13
236: 12
237: 11
238: 12
239: 11
240: 11
241: 10
242: 10
243: 10
244: 10
245: 9
246: 9
247: 9
248: 9
249: 8
250: 8
251: 8
252: 8
253: 7
254: 8
255: 7
256: 6
257: 7
258: 7
259: 6
260: 6
261: 6
262: 6
263: 6
264: 5
265: 6
266: 5
267: 5
268: 5
269: 5
270: 4
271: 5
272: 4
273: 5
274: 4
275: 4
276: 4
277: 4
278: 4
279: 3
280: 4
281: 3
282: 4
283: 3
284: 3
285: 4
286: 3
287: 3
288: 3
289: 2
290: 3
291: 3
292: 2
293: 3
294: 2
295: 3
296: 2
297: 3
298: 2
299: 2
300: 2
301: 2
302: 2
303: 2
304: 2
305: 2
306: 2
307: 2
308: 1
309: 2
310: 2
311: 1
312: 2
313: 1
314: 2
315: 1
316: 2
317: 1
318: 2
319: 1
320: 1
321: 1
322: 2
323: 1
324: 1
325: 1
326: 1
327: 1
328: 1
329: 1
330: 1
331: 1
332: 1
333: 1
334: 1
335: 1
336: 1
337: 1
338: 1
340: 1
341: 1
342: 1
344: 1
345: 1
347: 1
348: 1
350: 1
351: 1
353: 1
355: 1
357: 1
359: 1
361: 1
363: 1
365: 1
367: 1
370: 1
373: 1
376: 1
379: 1
382: 1
386: 1
389: 1
394: 1
399: 1
404: 1
410: 1
417: 1
425: 1
436: 1
449: 1
467: 1
497: 1
592: 1
此后全部幸存，不再有死亡案例

复制代码

以上死亡次数相加，得到存活$100$行之后还要死$33002$次，剩余的存活次数为$78926853$次，

所以当$p=0.75$时，数字$1$的存活概率约为$0.78926853$。

#####

玩$6$亿次游戏，再次进行数值分析，得到剩余的存活次数为$473614448$次，

所以当$p=0.75$时，数字$1$的存活概率约为$0.78935741$。

KeyTo9_Fans · 发表于 2018-2-5 11:06:27

问题$2$：要令生存概率为$0$，$p$的最大值是多少？

取$p=0.74$，玩$3$亿次游戏，求得生存概率为$0.74649012$；

取$p=0.73$，玩$3$亿次游戏，求得生存概率为$0.68895148$；

取$p=0.72$，玩$10$亿次游戏，求得生存概率为$0.600599344$；

取$p=0.71$，玩$5$亿次游戏，求得生存概率为$0.435693792$；

把以上$5$个数据点用一条曲线连起来，就得到了这样的结果：

于是就可以目测出$p$的临界值大概是$0.698$了。

#####

取$p=0.7$，玩$5$亿次游戏，求得生存概率为$0$

说明上述预测方法很不靠谱，正确的阈值应该介于$0.7$到$0.71$之间，而不是$0.698$

取$p=0.705$，玩$2$万次游戏，求得生存概率依然为$0$

说明正确的阈值应该介于$0.705$到$0.71$之间，与上述预测方法的结果相去甚远，还不如用二分法求临界值

取$p=0.706$，玩$2$万次游戏，求得生存概率明显大于$0$，

说明正确的阈值应该介于$0.705$到$0.706$之间。

取$p=0.7055$，玩$300$次游戏，求得生存概率略大于$0$，

说明正确的阈值应该介于$0.705$到$0.7055$之间。

取$p=0.7054$，玩$200$次游戏，求得生存概率为$0$，

说明正确的阈值应该介于$0.7054$到$0.7055$之间。

KeyTo9_Fans · 发表于 2018-2-6 01:19:49

由于我们已经拿到了$p$的临界值的足够多的小数位数（$4$位小数）了，

我们接下来就可以去维基百科的《渗流阈值》词条里用【Ctrl+F】查找文本【0.7054】了。

不出所料，搜出来一张表：

里面已经有$4$条记录了，分别对应$4$篇参考文献。

其中，最准确的结果是$0.70548522(4)$，来自参考文献[180]，摘录如下：

$1999$年发表的，现在已经$2018$了，我彻底out了。

参考文献：

[180] Jensen, Iwan (1999). "Low-density series expansions for directed percolation: I. A new efficient algorithm with applications to the square lattice". J. Phys. A. 32 (28): 5233–5249.

账号		自动登录	找回密码
密码			欢迎注册

[原创] 数字"1"在三角阵中的生存概率

点评

点评