- 注册时间
- 2014-9-4
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 42
- 在线时间
- 小时
|
马上注册,结交更多好友,享用更多功能,让你轻松玩转社区。
您需要 登录 才可以下载或查看,没有账号?欢迎注册
×
浙大工程硕士概率统计题目,毕业十几年了,实在不懂,希望有解答过程。
- 设连续型随机变量 \(X\) 满足:当 \(0\lt x\leq 1\) 时,\(P(0\lt X\leq x)=\frac{x^2}{2}\),当 \(2\lt x\leq 3\) 时,\(P(0\lt X\leq x)=\frac{(x-2)^2}{2}\)。
求 \(X\) 的分布函数及密度函数。 - 设随机变量 \((X,Y)\) 的概率密度 \(f(x,y)=\begin{cases}xy/2,&0\lt x\lt2,\ 1\lt y\lt1\\(2-x)y/6, &0\lt x\lt2,\ 1\lt y\lt2\\0,&\text{其它}\end{cases}\),
求: (1) \(P(X+Y>1)\) (2) \(F(x,y),\;F(1,1.5)\) (3) \(f_X(x),\;f_Y(y)\) (4) \(f_{Y|X}(y|x)\)

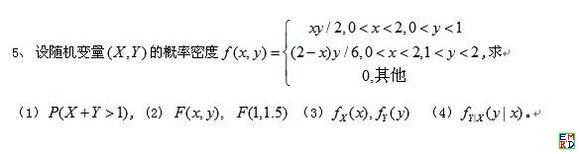
|
评分
-
查看全部评分
|