- 注册时间
- 2013-10-24
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 8858
- 在线时间
- 小时
|
 发表于 2014-11-5 22:13:14
|
显示全部楼层
发表于 2014-11-5 22:13:14
|
显示全部楼层
本帖最后由 kastin 于 2014-11-5 22:14 编辑
弹性力学倒是需要较强的数学功底,毕竟需要解出应力函数(平衡方程是一组偏微分方程组),而且很多解都是级数解或者带半猜测性质的,不过做起来挺有意思的,而且复变函数中的很多知识也能用到求解应力函数的中。但材料力学就简单多了,它是弹性力学的简化版,做了很多假设,所以用的都是很简单微积分知识。
考虑一个长为 `l` 的等截面均匀水平悬臂梁(或细杆),在自由端施加竖直向下的集中力 `F`,经变形后达到静平衡。
以悬点为原点,水平向右为 `x` 轴,竖直向下为 `y` 轴建立坐标系。设距离原点水平距离为 `x` 处竖直位移为 `y(x)`。在沿竖直方向截断梁(或杆),显然截面处内力只有弯矩。对右边一段受力分析可知,截面处的弯矩与外力平衡,所以弯矩 `M(x)=F(l-x)`.
所以$$\kappa=\frac{y''}{(1+y'^2)^{3/2}}=\frac{F(l-x)}{EI}\tag{1}$$下面考虑边值条件,在固定端,位移为零:`y(0)=0`;固定端不会发生转动,仍然保持原来水平角度:`y'(0)=0`.
事实上,上述公式左端(也就是9楼给出的公式)有很强的几何意义。因为曲率的定义是,曲线切线的转角 `\theta` 相对于弧长 `s` 的变化率,并注意到弧微分关系 `ds=\sqrt{1+y'^2}\,dx` 和几何关系`\theta=\arctan y'`,因此就有$$\kappa=\frac{d\theta}{ds}=\frac{dy'}{(1+y'^2)\sqrt{1+y'^2}dx}=\frac{y''}{(1+y'^2)^{3/2}}\tag{2}$$
1. 若变形较小,最大转角 `y'\to 0`,故(1)可近似为 `EI y''=F(l-x)`,积分可得 `\D y=-\frac{F}{6EI}x^3+\frac{Fl}{2}x^2+c_1x+c_2`,代入边界条件得到挠曲线(变形后的曲线)方程$$y=-\frac{F}{6EI}x^3+\frac{Fl}{2}x^2$$这是一个三次曲线。
2. 这次我们换个稍微精确一点的近似方法来处理(思想来自于8楼资料)。注意到弧微分关系可变形为$$\frac{dy}{dx}=\pm \frac{dy/ds}{\sqrt{1-(dy/ds)^2}}\tag{3}$$如果我们能从等式(1)和(2)中得到 `dy/ds` 的近似表达,那么代入方程(3)后,相当于将方程(1)降为了一阶。
为方便起见,记 `\D a=\frac{F}{2EI}`。因为有小角度近似 `\arctan y'\sim y'\,(y'\to 0)` 代入(2)得到$$\frac{d\theta}{ds} \sim \frac{dy'}{ds}=\frac{d(dy/dx)}{ds}\stackrel{\color{green}{(a)}}{=}\frac{d^2y}{dxds}\stackrel{\color{green}{(b)}}{=}\frac{d(dy/ds)}{dx}=2a(l-x)\tag{4}$$因为 `s=0` 时 `s=x`,故`\D \frac{dy}{ds}|_{s=0}=\frac{dy}{dx}|_{s=0}\*\frac{ds}{dx}|_{x=0}=0\* 1=0`因此$$\frac{dy}{ds}=\frac{dy}{ds}|_{s=0}+\int_0^x 2a(l-u)\dif u=a(2lx-x^2)$$于是,将结果代入(3)便得到稍精确降阶微分方程$$\frac{dy}{dx}=\pm \frac{2alx-ax^2}{\sqrt{1-(2alx-ax^2)^2}}\tag{*}$$使用Mathematica求解(物理解满足转角 `y'>0`,前面取正号 ). 上述方程都没有解析解,通过Mathematica数值求解 `a=3,l=1` 得到结果
- s1 = NDSolveValue[{y''[x] == 3 (1 + y'[x]^2)^(3/2) (1 - x), y[0] == 0,
- y'[0] == 0}, y, {x, 0, 0.5}];
- s = NDSolveValue[{y'[x] == 3 (2 x - x^2)/Sqrt[1 - 3^2 (2 x - x^2)^2],
- y[0] == 0}, y, {x, 0, 0.5}];
- Plot[{s1[x], s[x]}, {x, 0, 0.4}, PlotLegends -> {"精确解", "近似解"}]
a(l-x)情形的解
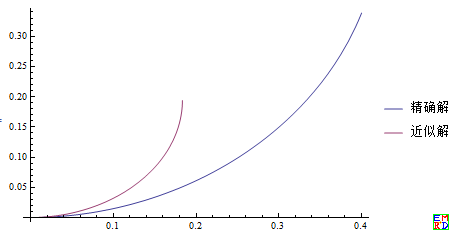
但是可以肯定的是,它们的解与椭圆积分有关,比如上面的积分,如果方程中的 `(l-x)` 换成 `x` 那么结果恰好就是第一类不完全椭圆积分 `F(x|m)` 和第二类不完全椭圆积分 `E(x|m)` 在参数 `m=-1` 时的复合函数 $$y=\frac{1}{\sqrt{a}}E(\arcsin(\sqrt{a}x)|-1)-\frac{1}{\sqrt{a}}F(\arcsin(\sqrt{a}x)|-1)\tag{5}$$Mathematica代码- sol1 = DSolve[{y'[x] == a x^2/Sqrt[1 - a^2 x^4], y[0] == 0}, y[x],
- x] // Simplify[#, a > 0] &
2. 若各个位置的位移(挠度)尺度跨度较大(非小变形)。
a. 但在原点附近,位移较小,并且转角接近零,即 `x \to 0,y' \to 0`,上述近似解都成立。
b. 在全局范围,则不能适用上述近似。直接求解方程(1),解有两个(一正一负),考虑到物理解必须满足 `y>0`,使用Mathematica计算出结果仍然是(5):- sol = DSolve[{y''[x] == 2 a (1 + y'[x]^2)^(3/2) x, y[0] == 0,
- y'[0] == 0}, y[x], x] // Simplify[#, a > 0]&
令`a=3`,绘图比较
- Plot[{y[x] /. sol1 /. a -> 3, y[x] /. First[sol] /. a -> 3}, {x, 0,
- 1}, PlotLegends -> {sol1[[1]][[1]] // TraditionalForm,
- First[sol][[1]] // TraditionalForm}]
ax情形的解
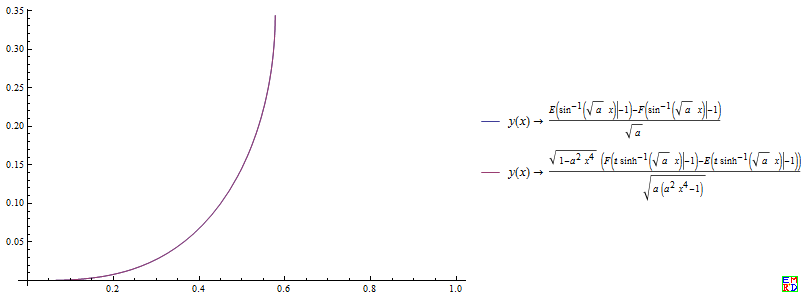
很显然,(*)与(1)不等价,这在上面的图像中给出了
我猜测,问题出在:要么Mathematica直接求解(1)给出的解只是一个分支,或者是某种情况下退化的解;要么(4)式中的步骤(a)或步骤(b)有问题(因为全微分不等于偏微分,弧长 `s` 也是坐标 `x` 的函数)。
下面回到能量法。弹性势能在弹性系统中指的就是应变能(条件是“完全弹性“,即能量不会损耗),因为势能对应保守系统,保守系统能量不会耗散,而是相互转化,且与路径无关,就意味着可全微分。弹性势能来自于弯矩做功。由于假设纯弯曲,所以只有弯曲应变能,单位弧长上转角为`\D\frac{1}{\rho}=\kappa`单位长度梁段弯矩做功(弯曲应变能密度)为`\D V_{\varepsilon}=\int_0^k M\dif k=\int_0^{\kappa} EIk\dif k=\frac{1}{2}EI\kappa^2=\frac{1}{2}EI\kappa^2=\frac{M^2}{2EI}`总能为整个梁的弧长积分$$V=\frac{1}{2}EI\int \kappa^2 ds $$即找到上述积分的最小值,而`\kappa`与变形曲线的关系就是$$\kappa=\frac{y''}{(1+y'^2)^{3/2}}$$这就相当于一个变分问题了。 |
|