特殊的共心三角形

数学星空

如下图,若三角形\(\triangle DEF\)在锐角\(\triangle ABC\)内部，且\(AD=BE=CF= r\)，\(D,E, F\)分别在线段\(AF，BD，CE\)上,设\(\triangle ABC\)各边长依次为\(a,b,c\)



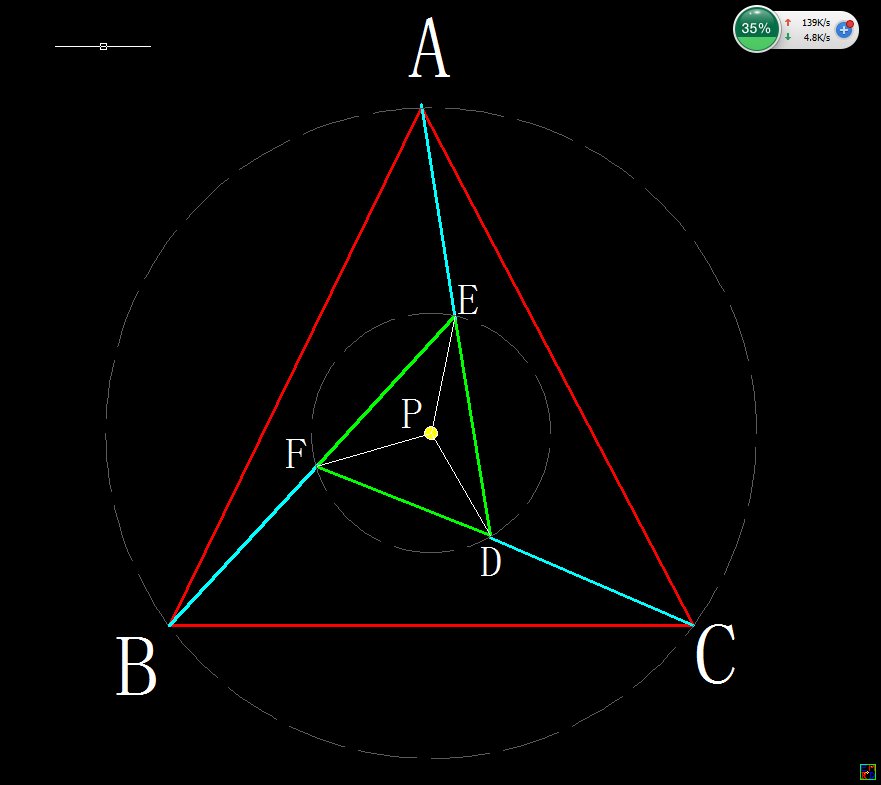
1)若存在点\(P\)是\(\triangle ABC\)和\(\triangle DEF\)的外心,求\(r\)值? 并给出\(\triangle DEF\)的各边长\(m,n,p\)?

2)若存在点\(P\)既是\(\triangle ABC\)的外心,又是\(\triangle DEF\)的内心,求\(r\)值? 并给出\(\triangle DEF\)的各边长\(m,n,p\)?

3)若存在点\(P\)既是\(\triangle ABC\)的外心,又是\(\triangle DEF\)的垂心,求\(r\)值? 并给出\(\triangle DEF\)的各边长\(m,n,p\)?

4)若存在点\(P\)既是\(\triangle ABC\)的外心,又是\(\triangle DEF\)的重心,求\(r\)值? 并给出\(\triangle DEF\)的各边长\(m,n,p\)?


5)若存在点\(P\)是\(\triangle ABC\)和\(\triangle DEF\)的内心,求\(r\)值? 并给出\(\triangle DEF\)的各边长\(m,n,p\)?

6)若存在点\(P\)既是\(\triangle ABC\)的内心,又是\(\triangle DEF\)的外心,求\(r\)值? 并给出\(\triangle DEF\)的各边长\(m,n,p\)?

7)若存在点\(P\)既是\(\triangle ABC\)的内心,又是\(\triangle DEF\)的垂心,求\(r\)值? 并给出\(\triangle DEF\)的各边长\(m,n,p\)?

8)若存在点\(P\)既是\(\triangle ABC\)的内心,又是\(\triangle DEF\)的重心,求\(r\)值? 并给出\(\triangle DEF\)的各边长\(m,n,p\)?


9)若存在点\(P\)是\(\triangle ABC\)和\(\triangle DEF\)的垂心,求\(r\)值? 并给出\(\triangle DEF\)的各边长\(m,n,p\)?

10)若存在点\(P\)既是\(\triangle ABC\)的垂心,又是\(\triangle DEF\)的外心,求\(r\)值? 并给出\(\triangle DEF\)的各边长\(m,n,p\)?

11)若存在点\(P\)既是\(\triangle ABC\)的垂心,又是\(\triangle DEF\)的内心,求\(r\)值? 并给出\(\triangle DEF\)的各边长\(m,n,p\)?

12)若存在点\(P\)既是\(\triangle ABC\)的垂心,又是\(\triangle DEF\)的重心,求\(r\)值? 并给出\(\triangle DEF\)的各边长\(m,n,p\)?



13)若存在点\(P\)是\(\triangle ABC\)和\(\triangle DEF\)的重心,求\(r\)值? 并给出\(\triangle DEF\)的各边长\(m,n,p\)?

14)若存在点\(P\)既是\(\triangle ABC\)的重心,又是\(\triangle DEF\)的外心,求\(r\)值? 并给出\(\triangle DEF\)的各边长\(m,n,p\)?

15)若存在点\(P\)既是\(\triangle ABC\)的重心,又是\(\triangle DEF\)的内心,求\(r\)值? 并给出\(\triangle DEF\)的各边长\(m,n,p\)?

16)若存在点\(P\)既是\(\triangle ABC\)的重心,又是\(\triangle DEF\)的垂心,求\(r\)值? 并给出\(\triangle DEF\)的各边长\(m,n,p\)?

若点\(P\)在一般条件不存在,请给出存在的条件?

注: \(EF=m,DF=n,DE=p\)

chyanog

问题1)，不存在这样的点P

creasson

以第一问为例：用重心坐标
\[\left\{ \begin{array}{l}
A  =  \frac{r}{m}E + \left( {1 - \frac{r}{m}} \right)D \\
B = \frac{r}{n}F + \left( {1 - \frac{r}{n}} \right)E \\
C = \frac{r}{p}D + \left( {1 - \frac{r}{p}} \right)F \\
\end{array} \right.\]
由距离公式得
\[\left\{ \begin{array}{l}
{c^2} = \frac{{{r^3}}}{m} + {r^2} - mr + \left( {1 - \frac{r}{m}} \right)\left\{ {\frac{r}{n}{p^2} + \left( {1 - \frac{r}{n}} \right){m^2} - nr + {r^2}} \right\} \\
{a^2} = \frac{{{r^3}}}{n} + {r^2} - nr + \left( {1 - \frac{r}{n}} \right)\left\{ {\frac{r}{p}{m^2} + \left( {1 - \frac{r}{p}} \right){n^2} - pr + {r^2}} \right\} \\
{b^2} = \frac{{{r^3}}}{p} + {r^2} - pr + \left( {1 - \frac{r}{p}} \right)\left\{ {\frac{r}{m}{n^2} + \left( {1 - \frac{r}{m}} \right){p^2} - mr + {r^2}} \right\} \\
\end{array} \right.\]
再由外心坐标公式：
\[P = \frac{{{a^2}\left( {{b^2} + {c^2} - {a^2}} \right)A + {b^2}\left( {{c^2} + {a^2} - {b^2}} \right)B + {c^2}\left( {{a^2} + {b^2} - {c^2}} \right)C}}{{2{a^2}{b^2} + 2{b^2}{c^2} + 2{c^2}{a^2} - {a^4} - {b^4} - {c^4}}}\]
\[P = \frac{{{n^2}\left( {{p^2} + {m^2} - {n^2}} \right)D + {p^2}\left( {{m^2} + {n^2} - {p^2}} \right)E + {m^2}\left( {{n^2} + {p^2} - {m^2}} \right)F}}{{2{m^2}{n^2} + 2{n^2}{p^2} + 2{p^2}{m^2} - {m^4} - {m^4} - {p^4}}}\]
代入比较可得如下两式:
\[\left\{ \begin{array}{l}
\frac{{{a^2}p\left( {m - r} \right)\left( {{b^2} + {c^2} - {a^2}} \right) + {c^2}mr\left( {{a^2} + {b^2} - {c^2}} \right)}}{{(2{a^2}{b^2} + 2{b^2}{c^2} + 2{a^2}{c^2} - {a^4} - {b^4} - {c^4})mp}} = \frac{{{n^2}\left( {{p^2} + {m^2} - {n^2}} \right)}}{{2{m^2}{n^2} + 2{n^2}{p^2} + 2{p^2}{m^2} - {m^4} - {m^4} - {p^4}}} \\
\frac{{{c^2}n\left( {p - r} \right)\left( {{a^2} + {b^2} - {c^2}} \right) + {b^2}pr\left( {{a^2} + {c^2} - {b^2}} \right)}}{{(2{a^2}{b^2} + 2{b^2}{c^2} + 2{a^2}{c^2} - {a^4} - {b^4} - {c^4})np}}   = \frac{{{m^2}\left( {{n^2} + {p^2} - {m^2}} \right)}}{{2{m^2}{n^2} + 2{n^2}{p^2} + 2{p^2}{m^2} - {m^4} - {m^4} - {p^4}}} \\
\end{array} \right.\]
以上五式共同决定未知数m,n,p,r