空间四球,每三球的外公切面交于一线,这四线是否共线

chyanog

假定球两两相离、半径不等，任意三球球心不共线，结论应该成立，如何证明？

hujunhua

证明：任意两个大小不等的相离圆球都有一个外公切锥，使得两球在同一个半锥内（vs 内公切锥，两球各处于一个半锥内）。
（注：两个对顶半锥构成一个向两方无限伸展的整锥)
将四个球记为A, B, C, D.
将A, B两球的外公切锥锥顶记为`V_{AB}`, 其余5个锥顶类此标记。
将A, B, C三球的外公切面交线记为`l_{ABC}`, 其余三条交线类此标记。
易知，
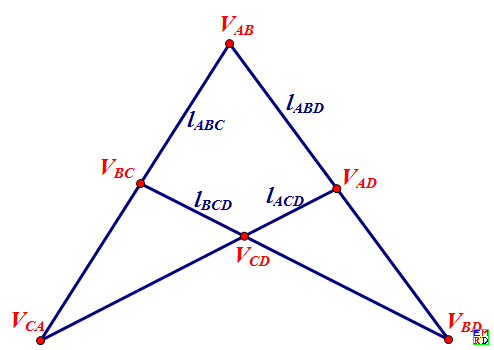
        交线`l_{ABC}`关联三个锥顶`V_{AB}, V_{BC}, V_{AC}`，
        交线`l_{ABD}`关联三个锥顶`V_{AB}, V_{BD}, V_{AD}`，
        交线`l_{ACD}`关联三个锥顶`V_{AC}, V_{AD}, V_{CD}`，
        交线`l_{BCD}`关联三个锥顶`V_{BC}, V_{BD}, V_{CD}`。
可见四条交线两两相交。我们知道空间三条直线两两相交则必定共面，所以这四条直线共面，见图。


后语：如果将命题改为六个锥顶共面可能更见精妙。