以概率1收敛（a.s.收敛）问题

fungarwai

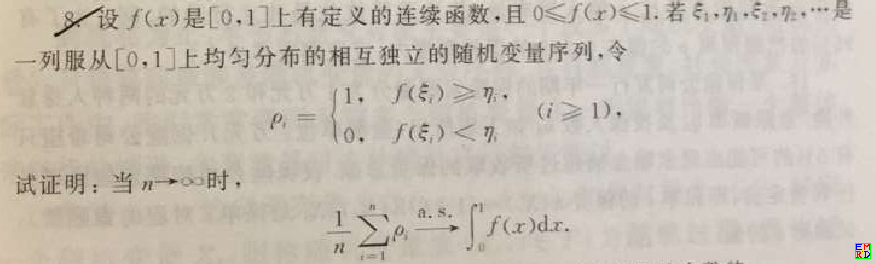
设 \(f(x)\) 是 \([0,1]\) 上有定义的连续函数，且 \(0\leqslant f(x)\leqslant 1\). 若 \(\xi_1,\eta_1,\xi_2,\eta_2,\dots\) 是一列服从 \([0,1]\) 上均匀分布的相互独立的随机变量序列，令 \[\rho_i=\begin{cases}1, &f(\xi_i)\geqslant\eta_i,\\0, &f(\xi_i)\lt\eta_i\end{cases}(i\geqslant1),\]
试证明：当 \(n\to\infty\) 时，\[\frac1n\sum_{i=1}^{n}{\rho_i}\ce{->[a.s.]}\int_0^1f(x)\dif x .\]