空心半球的万有引力函数不连续

TSC999

在数学教科书上总能看到各种各样的奇怪函数，例如有一种是这样的意思：
在某一点 x = x0  处，函数值 f(x0) =10，当 x 比 x0 减少一丁点儿，f(x) 就会突然上跳成 30；而当 x 比 x0 增加一丁点儿，f(x) 又会突然下跳成 -10。
也就是说，在 x0 点处这个函数是不连续的，并且 f(x0) 的值等于该点的 ”左极限“ 与 ”右极限“ 的平均值。
我曾想，书本里面写的这种函数只是数学家们凭空臆想的怪物，在现实世界中是不会有这种不连续的怪现象的。但是现在的我不再这样认为了，也许真地有人在某时某地，突然掉进 ”时空隧道“ 中消失了。
你算一算这个空心半球的万有引力函数，就知道在顶点 A 处的不连续现象并非是人们的虚构。
注： 计算放在 x 轴上的一个质点受到的空心半球（有一定质量）的引力时，当质点受力方向沿 x 轴向时算正引力，否则算是负引力。这样规定以后，若质点位于负 x 轴上并且距离球心较远（大于球半径）时，
该质点所受引力为正值。而当质点从左到右移动到正 x 轴上时，它受到的引力将变为负值。从正到负，这中间的变化过程是连续的吗？假定空心球壳是无限薄的、没有厚度的。

kastin

连续，但可能是分段函数（存在不可导的衔接点）。

kastin

设引力常量为 `G`，半圆半径为 `R`，质量线密度为 `\rho`，以 `y` 轴为极轴，逆时针为正方向，极角为  `\theta` 处的微元弧质量为 `\dif m=\rho R\dif\theta`.
于是位于 `x(>0)` 处的单位质量质点与上述微元距离 `l` 满足余弦定理$$l=\sqrt{R^2+x^2-2xR\cos(\frac{\pi}{2}+\theta)}=\sqrt{R^2+x^2+2xR\sin\theta}$$设 `l` 所在直线与x轴夹角为 `\varphi`，现在的任务是计算 `\cos\varphi`. 同样根据余弦定理$$\cos\varphi=\frac{x^2+l^2-R^2}{2xl}=\frac{x+R\sin\theta}{\sqrt{R^2+x^2+2xR\sin\theta}}$$经检验，`x<0` 时上述结果仍然成立。
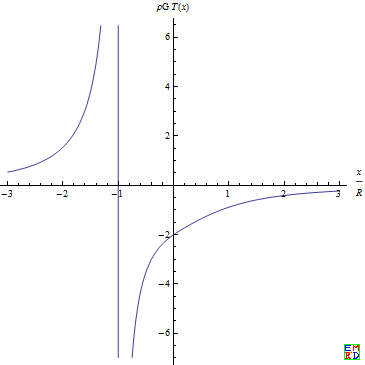
对称微元对单位质量质点的引力的合力为$$-2\cos\varphi\dif F=-\frac{2G}{l^2}\cos\varphi\dif m=\frac{2\rho RG(x+R\sin\theta)}{(R^2+x^2+2xR\sin\theta)^{3/2}}\dif \theta$$积分就得到总引力为$$T(x)=-2\rho G\int_0^{\frac{\pi}{2}}\frac{R(x+R\sin\theta)}{(R^2+x^2+2xR\sin\theta)^{3/2}}\dif \theta$$这个积分没有初等原函数，但如果 `t=x/R\neq 1`，还是可以用广义超几何函数以及椭圆积分函数来表达的:$$T(x)=-2 G \rho  \left[\frac{\left(t^2+1\right)\, _3F_2\left(\frac{3}{4},1,\frac{5}{4};\frac{1}{2},\frac{3}{2};\frac{4 t^2}{\left(t^2+1\right)^2}\right)-3 t^2 \, _3F_2\left(1,\frac{5}{4},\frac{7}{4};\frac{3}{2},\frac{3}{2};\frac{4 t^2}{\left(t^2+1\right)^2}\right)}{\left(t^2+1\right)^{5/2}}+\frac{(t-1) K\left(\frac{4 t}{(t+1)^2}\right)+(t+1) E\left(\frac{4 t}{(t+1)^2}\right)}{2 (t-1) t \left| t+1\right| }\right]\;(t=x/R)$$当 `t=-1` 时，无定义是因为 `x=-R`相当于单位质量质点与半圆环发生接触，此时单位质量物体不能继续被视为质点，引力公式失效。
当 `t=1` 时，上述公式不再有效，需要直接计算

1. -G \[Rho] Integrate[2(1 +
   
2.      Sin[\[Theta]])/(1 + 1^2 + 2*1* Sin[\[Theta]])^(3/2), {\[Theta],
   
3.    0, Pi/2}]

复制代码

结果为$$2\rho G\,\mathrm{arctanh}(1-\sqrt{2})=-\frac{1}{4}\ln (17+12\sqrt{2})\rho G$$引力结果绘图如下

TSC999

先说说我的计算结果吧。见下图：

TSC999

具体计算过程，今天没有时间了，以后慢慢发上来跟各位讨论吧。
由红色曲线关于纵轴对称可知，处于空心球壳（壳体可有任意厚度）内的物体，受球壳引力的和将为零。
由此知道，人站在地球表面时所受的引力最大，如果朝地心打个洞，人进到洞里越深，受的引力将随下潜深度成正比减小，到达地心时减到零。为什么会这样？因为人朝着地心进发时，他背后的球壳对他的引力相互抵消掉了。

zeroieme

事实上就是动点与半球与X轴交点距离趋0，$r^(-2)$这个负幂函数引起的跳跃。

可以拓展问题，半球上开个隧道供人/物体通过，然后分析隧道半径变化引起的变化。

kastin

zeroieme 发表于 2016-12-5 01:18
事实上就是动点与半球与X轴交点距离趋0，$r^(-2)$这个负幂函数引起的跳跃。

可以拓展问题，半球上开个隧 ...

上面已经说了，在与球壳接触点不能使用引力公式的，因为那时候已经不能看成质点，所以那里本身没有定义。

TSC999

为了计算引力，先建立坐标系如图。将半球面的球心放在坐标原点上，顶点 \( A~ \)朝左，底面在 \( YOZ~ \)平面内。假定球面的半径为 \( ~R=1~ \)，则半球面的方程为：
\( ~~~~~~~~~~~~~~~~~~~~~~~~~~  x^2+y^2+z^2=1 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(1)   \)
我们的问题就是计算放在 \( x \) 轴的一个质点，当它沿 \( x \) 轴从左向右 (或从右向左) 移动时（我们可以想象自己乘一架飞机沿 \( x \)轴飞行，飞机相对于半球面小得可以看做是一个质点），它受到的半球面的引力将怎样变化，特别是在图中 \( A \)点处，引力是否连续。

TSC999

        假定质点的质量为  \( m \)，球面的质量面密度为  \( μ \)，我们要规定该质点受到球面引力的 “正方向”：当质点受到的引力方向沿  \( x \) 轴正向时，认为引力为 “正”，而与  \( x \) 方向相反时，认为引力为 “负”。
在动手计算之前，先让我们凭 “直觉” 定性地猜测引力曲线的大致形状吧。
        当质点位于正  \( x \) 轴上、并且离坐标原点很远时，质点受半球面的吸引，方向沿负  \( x \) 轴，因此这时的引力是 “负”的；当质点位于负  \( x \) 轴上、并且离坐标原点很远时，质点受半球面的吸引，方向沿正  \( x \) 轴，这时的引力是 “正” 的。
现在的问题是，“正” 曲线与 “负” 曲线如何交汇呢？有人认为，它们大概是在半球面的 “重心” 处交汇：在该点，质点受到的引力是零。定性地画出引力曲线如图 2 所示。这条想象中的引力曲线是连续的。
        然而，这条曲线画得并不正确。

TSC999

        下面让我们用积分方法定量地进行分析和计算，看引力曲线到底应该是什么样子。
        
        如图  \( 3 \)，当质点在\(~ B~ \)点时，假定它到坐标原点的距离为 \( a \)，沿 \( y \) 轴和 \( z \)轴方向的合成引力均为零，只有沿 \( x \) 方向（或负 \( x \)方向）的引力 \( F_x \)，为了求出这个引力，可以用一系列平行于 \(YOZ\) 的平行平面（相互间距为 \(dx\) ）切割半球面，将其切成许许多多的 “球带”。每一个球带的表面积均为：
\(  ~~~~~~~~~~~~~~~~~~~~~dS=2πRdx=2πdx ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(2)   \)
        注意，\( dS \)  的大小与它所处的位置 \( x \) 无关，只与球半径 \( R \) 和 \(dx \) 有关。这一点，许多教科书中似乎没有强调，甚至根本就没有提过这个不起眼的公式。
        根据万有引力的计算公式，\( F_x \) 可表达为下面的面积分：
\(~~~~~~~~~~~~~~~~~~~~ F_x= \int_s \frac{kmμdS}{L^2}*\frac{(x-a)}{L}  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(3)       \)
        上式中 \( k \) 是万有引力常数。\( x \) 是 \( dS \) 球带的横坐标。\( L \) 是 \( B \) 点（质点在此处）到 \( dS \) 面上任一点的距离。\( \frac{(x-a)}{L}=cosθ  \)，表示引力要投影到 \( x \) 轴上才能 “合成” 到 \( F_x \) 中。
         根据空间两点间的距离公式:
         \( ~~~~~~~~~~ L=\sqrt{(x-a)^2+y^2+z^2 }   ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(4)                        \)
         由 \( (1) \) 式，\(  z^2=\sqrt{1-x^2-y^2} \)，代入上式并考虑到  \( y=0  \)，上式可简化为：
         \( ~~~~~~~~~~ L=\sqrt{1+a^2-2ax}   ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(5)                        \)
        设 \(  kmμ=1 \) ，将 \(（5）、（2）\) 代入 \(（3）\) 式中，得：
        \(~~~~~~~~~~~  F_x=2π \displaystyle \int_{-1}^{0} \frac{(x-a)dx}{(1-2ax+a^2)^{3/2}} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(6)                \)
        先做上式的定积分，积分结果为：
        \(~~~~~~~~~~~~~~ 2π\frac{1}{a^2 \sqrt{1+a^2}}-2π\frac{1+a}{\sqrt{(1+a)^2}} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(7)      \)
        当 \( -1<a<+∞ \) 时，\( (7) \) 式简化为：
\(~~~~~~~~~~~~~~~~~~~~~  F_x= \frac{2π}{a^2}(\frac{1}{\sqrt{1+a^2}}-1) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(8)                \)
        当 \( -∞<a<-1 \) 时，\( (7) \) 式简化为：
\(~~~~~~~~~~~~~~~~~~~~~  F_x= \frac{2π}{a^2}(\frac{1}{\sqrt{1+a^2}}+1) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(9)                \)
        当 \( a=-1 \) 时，表示质点恰好放在半球面的顶点 \( A \) 处（见图1）。注意，此时 \( (7) \) 式中第二项的分母为零，公式不能用。这时要重新考虑 \( (6) \) 式的积分。
        将 \( a=-1 \) 代入  \( (6) \) 式得：
\(~~~~~~  F_x=2π \displaystyle \int_{-1}^{0} \frac{(x-a)dx}{(1-2ax+a^2)^{3/2}}= 2π \displaystyle \int_{-1}^{0} \frac{(x+1)dx}{(1+2x+1)^{3/2}}=\\~~~~~~~~~=2π \displaystyle \int_{-1}^{0} \frac{(x+1)dx}{2^{3/2}(1+x)^{3/2}}= \frac{2π}{\sqrt{8}}\displaystyle \int_{-1}^{0} \frac{dx}{\sqrt{1+x}}=\sqrt{2}π ~~~~~~~~~~~~~~~~(10)                \)

        \(  (8)、(9)、(10) \) 三式就是所求的结果。按此做出的引力曲线如下图所示：