落叶高精度表达式计算器v1.0版

落叶 · 发表于 2016-12-28 19:57:14

本帖最后由落叶于 2016-12-28 19:59 编辑

happysxyf 发表于 2016-12-28 19:14
表达式解析，最好还是用逆波兰特最简单，速度最快，内存占用最小，我实现表达式计算只要3小时。但是我不 ...

天哪，你表达式实现只要了三小时，你知道我构思基本通过用了多少？用了两个月，中间完善大概四个月吧，就这样我还觉得不可思议，感觉太快了！

happysxyf · 发表于 2016-12-29 12:02:03

落叶发表于 2016-12-28 19:33
http://bbs.emath.ac.cn/thread-8882-2-1.html这里有我向宝宝请教对数的贴子，我的主题里有对三角函数的学 ...

好的，感谢提供思路，因为逆波兰特是几乎所有现代计算机的实现方式。太经典，所以必须得用。

落叶 · 发表于 2016-12-29 17:20:36

本帖最后由落叶于 2016-12-29 20:15 编辑

我已过了需要表扬的年龄了，首先在这里第一个发布，就是来让网友们批评，指正的，错误啥的大量接收!

happysxyf · 发表于 2016-12-30 19:02:44

本帖最后由 happysxyf 于 2016-12-30 19:06 编辑

落叶发表于 2016-12-29 17:20
我已过了需要表扬的年龄了，首先在这里第一个发布，就是来让网友们批评，指正的，错误啥的大量接收!

落叶，你的计算器非常好用，暂无漏洞。圆周率很快，准确无误。
但是居然没有排列组合数，这个经常需要用到。

落叶 · 发表于 2016-12-31 02:00:41

本帖最后由落叶于 2016-12-31 02:05 编辑

整体框架现比较完善，加功能很方便的，批量计算已想好，1.1版再加上，发现一个问题，x的负一次方忘了判断，现计算是错的。
那个圆周率我没有计算，存了一个万位常数直接读取。

happysxyf · 发表于 2016-12-31 11:02:17

落叶发表于 2016-12-31 02:00
整体框架现比较完善，加功能很方便的，批量计算已想好，1.1版再加上，发现一个问题，x的负一次方忘了判断， ...

怪不得计算派都不需要时间，直接就出来了。

落叶 · 发表于 2017-1-2 15:47:51

本帖最后由落叶于 2017-1-2 19:56 编辑

刚才简单的和SpeedCrunch（老外的成品计算器）在表达式解析方面作了一下测试，（国内的还没找到合适的）
sin(5)
= -0.95892427466313846889

((((((((2^2)*2)^2)*2)^2)*2)^2)^2)*2
= 2305843009213693952

-((((((((2^2)*2)^2)*2)^2)*2)^2)^2)*2
= -2305843009213693952

23+56/(102-100)*((36-24)/(8-6))
= 191

1.55- 1.55^3/3! +1.55^5/5! - 1.55^7/7!+ 1.55^9/9!
= 0.99978682495119270984

1.55- 1.55*1.55^2*(4*5*6*7*8*9 - 1.55^2*(6*7*8*9 - 1.55^2*(8*9- 1.55^2)))/9!
= 0.99978682495119270984

sin(6)+3
= 2.72058450180107412719

cos(sin(6)^4)^6
= 0.99988854394413890284

cos (sin(6)^ 4)^ 6
= 0.99988854394413890284

cos(sin(-6)^4)^6
= 0.99988854394413890284

cos(-sin(6)^4)^6
= 0.99988854394413890284

2^cos(sin(6)^4)^6
= 1.9998454950664980933

上面有红色部分和我的不一致：
我的是：2^cos(sin(6)^4)^6  =6.3995055612514362198736651007398E1
然后加上括号后：2^(cos(sin(6)^4)^6 )  =1.9998454950664980933018590689861，这时才和它的结果保持一致，
不知道从语法上到底是谁才是对的？
SpeedCrunch的:2^sin(3)^2= 1.01389964085539956385,我的：2^sin(3)^2  =1.216081581587201296984729037121值不同
2^sin(3)*2= 2.20552178097356481036但这个数 SpeedCrunch的和我一致，看来它采用的是乘方指数优先原则。

落叶 · 发表于 2017-1-2 16:36:01

本帖最后由落叶于 2017-1-2 21:46 编辑

在算4^4!时：
SpeedCrunch的是4^4!= 281474976710656，很明显它是先算了后面的。
我目前把两个运算符的等级定为相等，所以我的是左边先算：4^4! =8.5781777534284265411908227168123E506
不知道两个运算符的数学运算等级是怎么样的，上网查了一下也没查出结果？
单操作数的运算等级应该高于双操作数的，看来它是对的，我的运算符等级需要重新调整一下。开始我把乘方运算定义为单操作数了

又查了一个国内比较牛的人写的表达式计算，运算4^4!采用的规则和它的一样。看来我需要改一下。好了，调了一下运算符等级，现在这个问题已解决。

落叶 · 发表于 2017-1-2 17:03:14

本帖最后由落叶于 2017-1-2 21:19 编辑

SpeedCrunch的3^4^2= 43046721
我的是：3^4^2 =6.561E3
难道两个乘方符号在一起先算右边的？

不过在我的计算器上有个等级最高的括号，若为了表达清晰，请把需要先算的括起来，就可以正常运算了。

又查了几个国内比较牛的人写的表达式计算，采用连续乘方的规则和我的一样。

happysxyf · 发表于 2017-1-3 13:20:54

本帖最后由 happysxyf 于 2017-1-3 17:25 编辑

落叶发表于 2017-1-2 17:03
SpeedCrunch的3^4^2= 43046721
我的是：3^4^2 =6.561E3
难道两个乘方符号在一起先算右边的？

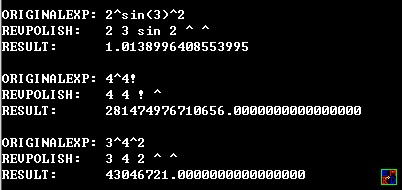
如果你使用逆波兰，你就没有这些问题了，我又花了几小时写了个逆波兰，这个的计算结果跟SpeedCrunch软件的完全吻合，运算优先级完全一致。只要你用逆波兰那些优先级都是一致的。只是我没加入高精度，其实大体框架已经成了。就差做个计算器的界面和按钮以及调用GMP的大数库提高点精度。

我的代码，本来只有100行，为了弄精致点变成了

/*
REVPOLISH.EXE
VERSION 1.0
*/
#include <stdio.h>
#include <ctype.h>
#include <math.h>
#include <windows.h>
/***************定义宏变量***************/
//堆栈尺寸
#define STACK_SIZE 1024
//数学函数关键词数
#define KEY_SIZE 23
//帮助说明
#define HELPINFORMATION "\
REVERSE POLISH EXPRESSION CALCULATOR, VERSION 1.0\n\
-----------------------------------------------------------------\n\
revpolish [expression]\n\
-----------------------------------------------------------------\n\
EXAMPLES:\n\
revpolish ((3*3+2)%6+7.187)*5-7/189+3^2\n\
revpolish (ceil(sin(pi/3)+2)%6+0.187)*e-lg(6.5)\n\
revpolish 5*(arctan(cos(sin(ln(lg(2.71828))))))\n\
-----------------------------------------------------------------\n\
FUNCTIONS:\n\
pi=3.1415926535897932, e=2.7182818284590452\n\
+, -, *, /, %, ^, !\n\
round, floor, ceil, exp, deg, sqrt, abs, lg, ln\n\
sin, cos, tan, arcsin, arccos, arctan\n\
sinh, cosh, tanh, arcsinh, arccosh, arctanh\n\
-----------------------------------------------------------------\n\
/***************全局类变量***************/
//数学函数关键词
static const char* KEY_WORDS[]={"arcsinh", "arccosh", "arctanh", "arcsin", "arccos", "arctan", "round", "floor", "ceil", "sqrt", "deg", "sinh", "cosh", "tanh", "lg", "ln", "sin", "cos", "tan", "abs", "exp", "e", "pi"};
static const char KEY_LLENS[]={ 7, 7, 7, 6, 6, 6, 5, 5, 4, 4, 3, 4, 4, 4, 2, 2, 3, 3, 3, 3, 3, 1, 2 };
//运算符栈
char STACK1[STACK_SIZE]={0};
//逆波兰栈
char STACK2[STACK_SIZE]={0};
//浮点数栈
double STACK3[STACK_SIZE]={0};
/***************功能函数类***************/
//判断逆波兰函数符，即大写字母
inline BOOL isLETTER(const char c)
{
if('A'<=c && c<='Z'){return TRUE;}
return FALSE;
}
//判断浮点数，包括小数点
inline BOOL isDDIGIT(const char c)
{
if( ('0'<=c&&c<='9') || c=='.'){return TRUE;}
return FALSE;
}
//阶乘函数
int fact(int n)
{
return (n<2) ?1 :n*(fact(n-1));
}
//识别关键词
char IdentifyKeyWords(char* pstr)
{
char SN;
for(SN=0; SN<KEY_SIZE; SN++){
char *op=pstr, *kp=(char*)KEY_WORDS[SN];
//比对字母
while(*op==*kp && *kp!='\0'){
op++, kp++;
}
//尾部验证
if((*op<'a'||*op>'z') && (*kp=='\0')){
return SN;
}
}
return -1;
}
//逆波兰核心
void RevPolishCore(const char* expression)
{
char *op=(char*)expression, *S1=STACK1, *S2=STACK2, SN;
double *S3=STACK3;
//逆波兰化
while(*op!='\0')
{
if(isspace(*op)){
op++;
continue;
}
//判断伪双目
if( (SN=IdentifyKeyWords(op)) !=-1)
{
*(S2++)='.';
*(S2++)=' ';
//伪双目入栈
while(isLETTER(*S1))
{
*(S2++)=*(S1--);
}
*(++S1)=SN+65;
op+=KEY_LLENS[SN];
continue;
}
switch(*op)
{
case '(':
*(++S1)=*op;
if(*(op+1)=='-' || *(op+1)=='+'){
*(S2++)='0', *(S2++)=' ';
}
break;
case ')':
while(*S1!='(')
{
*(S2++)=*(S1--);
}
//舍弃'('
S1--;
break;
case '+':
case '-':
while(S1!=STACK1 && *S1!='(')
{
*(S2++)=*(S1--);
}
*(++S1)=*op;
break;
case '^':
while(isLETTER(*S1))
{
*(S2++)=*(S1--);
}
*(++S1)=*op;
break;
case '!':
*(S2++)=*op;
break;
case '%':
case '*':
case '/':
while(isLETTER(*S1) ||*S1=='%' ||*S1=='*' ||*S1=='/' ||*S1=='^')
{
*(S2++)=*(S1--);
}
*(++S1)=*op;
break;
default :
//浮点数入栈
while(isDDIGIT(*op)){
*(S2++)=*(op++);
}
op--;
*(S2++)=' ';
break;
}
op++;
}
while(S1 !=STACK1)
{
*(S2++)=*(S1--);
}
*S2=' ';
//计算逆波兰
op=STACK2;
while(*op!=' ')
{
//计算伪双目
if(isLETTER(*op))
{
switch(*op)
{
case 'A':
*(S3-1)=asinh(*S3);
break;
case 'B':
*(S3-1)=acosh(*S3);
break;
case 'C':
*(S3-1)=atanh(*S3);
break;
case 'D':
*(S3-1)=asin(*S3);
break;
case 'E':
*(S3-1)=acos(*S3);
break;
case 'F':
*(S3-1)=atan(*S3);
break;
case 'G':
*(S3-1)=round(*S3);
break;
case 'H':
*(S3-1)=floor(*S3);
break;
case 'I':
*(S3-1)=ceil(*S3);
break;
case 'J':
*(S3-1)=sqrt(*S3);
break;
case 'K':
*(S3-1)=(*S3)*3.1415926535897932/180.0;
break;
case 'L':
*(S3-1)=sinh(*S3);
break;
case 'M':
*(S3-1)=cosh(*S3);
break;
case 'N':
*(S3-1)=tanh(*S3);
break;
case 'O':
*(S3-1)=log10(*S3);
break;
case 'P':
*(S3-1)=log(*S3);
break;
case 'Q':
*(S3-1)=sin(*S3);
break;
case 'R':
*(S3-1)=cos(*S3);
break;
case 'S':
*(S3-1)=tan(*S3);
break;
case 'T':
*(S3-1)=(*S3<0)?(-(*S3)):(*S3);
break;
case 'U':
*(S3-1)=exp(*S3);
break;
case 'V':
*S3=2.7182818284590452;
break;
case 'W':
*S3=3.1415926535897932;
break;
default :
break;
}
if(*op!='V' && *op!='W'){S3--;}
op++;
continue;
}
//计算双目
switch(*op)
{
case '+':
*(S3-1)+=*S3;
S3--;
break;
case '-':
*(S3-1)-=*S3;
S3--;
break;
case '*':
*(S3-1)*=*S3;
S3--;
break;
case '%':
case '/':
if(S3 !=STACK3){
if(*op=='%'){
*(S3-1)=(int)*(S3-1) % (int)*S3;
}else{
*(S3-1)/=*S3;
}
}else{
//除数为0，抛出错误并退出
fputs("Divisor is zero error\n", stderr);
exit(0);
}
S3--;
break;
case '^':
*(S3-1)=pow(*(S3-1), *S3);
S3--;
break;
case '!':
*S3=fact((int)(*S3));
break;
default :
//集数器
if (isDDIGIT(*op)){
*(++S3)=atof(op);
}
while(isDDIGIT(*op)){
op++;
}
break;
}
op++;
}
//打印中缀式
fprintf(stdout, "ORIGINALEXP: %s\n", expression);
//打印后缀式
fprintf(stdout, "REVPOLISH: ");
op=STACK2;
while(op!=S2){
if(*op=='.' && *(op+1)==' '){
op++;
}else if(isLETTER(*op)){
fprintf(stdout, "%s ", KEY_WORDS[*op-65]);
}else{
fputc(*op, stdout);
if(*op=='+' ||*op=='-' ||*op=='*' ||*op=='/' ||*op=='%' ||*op=='^' ||*op=='!'){fputc(' ', stdout);}
}
op++;
}
fputc('\n', stdout);
//打印计算结果
fprintf(stdout, "RESULT: %.16lf\n", *S3);
}
/*************MAIN主函数入口*************/
int main(int argc, char** argv)
{
if(argc==1){
//异常则抛出使用说明
fputs(HELPINFORMATION, stderr);
exit(1);
}
RevPolishCore(argv[1]);
return 0;
}

复制代码

300行：

以下是说明

用法：
-----------------------------------------------------------------------------
revpolish [expression]
-----------------------------------------------------------------------------
示例:
revpolish ((3*3+2)%6+7.187)*5-7/189+3^2
revpolish (ceil(sin(pi/3)+2)%6+0.187)*e-lg(6.5)
revpolish 5*(arctan(cos(sin(ln(lg(2.71828))))))
-----------------------------------------------------------------------------
备注：
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
常数类
pi 3.1415926535897932
e 2.7182818284590452
通用类
round 四舍五入
floor 整取
abs 绝对值
ceil 向上舍入
deg 角度转弧度
exp e的次幂
sqrt 开方
fac 阶乘
lg 常用对数，以10为底
ln 自然对数
+ 加
- 减
* 乘
/ 除
% 取余数
^ 次方
! 阶乘
三角函数类
sin、cos、tan
arcsin、arccos、arctan
双曲函数类
sinh、cosh、tanh
arcsinh、arccosh、arctanh
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

复制代码

源码都是完整的，直接就能编译，如果你的机器无法编译C语言请下载我的附件。我就差个高精度和计算器按钮界面了。

账号		自动登录	找回密码
密码			欢迎注册

[原创] 落叶高精度表达式计算器v1.0版

点评

点评