尺规作图

northwolves

用圆规作出两条线段AB,CD之差(两线段只给出了4个端点,且长短相近)

northwolves

没有办法？

mathe

建议找一本关于反演变换的书看看，应该可以完全解决圆规作图问题。

shshsh_0510

记得小时候看过这个，结论好像是所有尺规作图都可单用圆规解
呵呵，当时是看不太懂的。

mathe

^_^，根据shshsh_0510给出的台湾的链接，找到一篇介绍无尺作图的文章：
http://www.math.sinica.edu.tw/ma ... le=ZDMwNC8zMDQwNw==

无心人

学习学习啊

mathe

看到有人在CSDN回答了关于圆规作图的方法，给出的就是反演法:
http://topic.csdn.net/u/20080721 ... f-55391ff0b119.html

也来无聊一下.楼主只用圆规的限制挺有意思.粗看起来,只用圆规能作的图要少于可同时使用直尺和圆规作的图.但早在18世纪意大利人Mascheroni就证明了一个颇让人震惊的事实: 只使用圆规,可以作出所有尺规作图法能作出的图(当然,只用圆规不能画直线,因此此定理的一个更准确的说法是: 所有用直尺和圆规能找到的点,都可以单独用圆规找到).

Mascheroni定理的证明比较繁琐,为免跑题不在此列出了.这里只解决楼主的题目: 只用圆规找到一个圆的圆心.为此,我们需要先实现两个基本工具: 延长直线和找反演点.

工具1(延长直线): 已知两个点A和B, 对任意自然数n>1,可以用圆规找到AB延长线上的点C,使得AC=n*BC
作法: 只需考虑n=2的情况, n>2的情况可反复利用n=2的作法解决.
用r表示AB长,作法如下:
1. 以B为圆心,r为半径画圆
2. 在此圆上,从A点开始,依次用圆规找到三个点P,Q,C,使得AP=PQ=QC=r
3. C点满足AC=2*BC,完毕.
证明: 只需注意三角形AOP, POQ, QOC都是正三角形.

工具2(找反演点). 设有一个以O为圆心,r为半径的圆,则对平面上异于O的任意一点P,P关于圆O的反演点Q是直线OP上的满足如下条件的点:
      OP*OQ = r^2  (Q与P在O的同侧)
作法: 已知O,r,P,让我们用圆规找到P的反演点Q
1. 以P为圆心,OP为半径画圆,与圆O相交于R和S两点(注*)
2. 分别以R和S为半径,以r为半径画圆,交于Q点(另一个交点是O)
3  Q就是P的反演点
证明: 三角形OPR和ORQ都是等腰三角形,并且共一个底角POR,因此它们是相似三角形,有
    OP/OR = OR/OQ,  亦即OP*OQ = OR^2 = r^2
下面为配图:

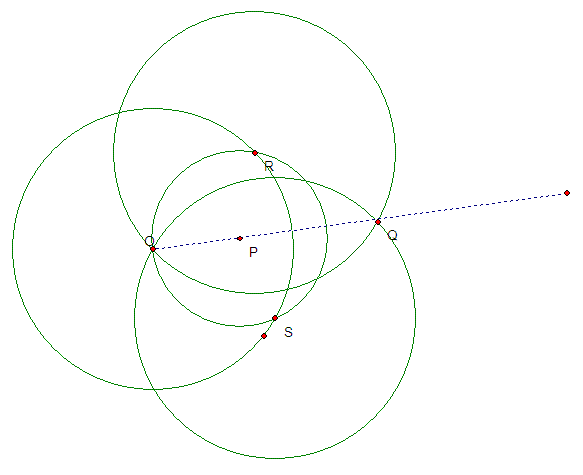*: 在第1步有一种情况需要考虑: 圆P与圆O不相交(P离O比较近的情况).此时可用工具1延长OP数倍,再找到新点的反演点,然后再把其延长相应的倍数即可.