- 注册时间
- 2015-10-15
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 2223
- 在线时间
- 小时
|
楼主 |
发表于 2017-4-30 10:27:24
|
显示全部楼层
本帖最后由 TSC999 于 2017-4-30 10:28 编辑
再来第二个例子,对于下面这个八区域,求其染色多项式:
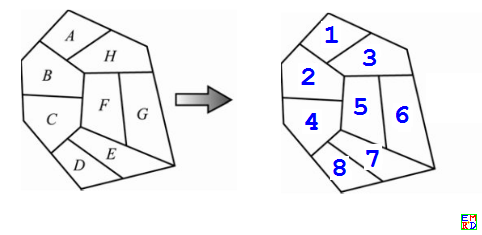
为求出上面区域的染色多项式,编程如下:
- Clear["Global`*"];
- Array[g, 20]; Array[c, 20];
- f[k_, m_, {}] := m^k
- For[i = 2, i <= 11, i++,
- f[k_, m_, s_] :=
- Module[{s1, s2, node1, node2}, node1 = s[[1]][[1]];
- node2 = s[[1]][[2]]; s1 = Delete[s, 1];
- s2 = Union[s1 /. node1 -> node2];
- f[k, m, s1] - f[k - 1, m, s2]
- ];
- s = Sort[{{1, 2}, {1, 3}, {2, 3}, {2, 4}, {2, 5}, {3, 5}, {3,
- 6}, {4, 5}, {4, 7}, {4, 8}, {5, 6}, {5, 7}, {6, 7}, {7, 8}}];
- g[i] = f[8, i, s];
- ];
- a = {a8, a7, a6, a5, a4, a3, a2, a1} /.
- NSolve[{a8 + a7 + a6 + a5 + a4 + a3 + a2 + a1 == g[2],
- a8 2^8 + a7 2^7 + a6 2^6 + a5 2^5 + a4 2^4 + a3 2^3 + a2 2^2 +
- a1 2^1 == g[3],
- a8 3^8 + a7 3^7 + a6 3^6 + a5 3^5 + a4 3^4 + a3 3^3 + a2 3^2 +
- a1 3^1 == g[4],
- a8 4^8 + a7 4^7 + a6 4^6 + a5 4^5 + a4 4^4 + a3 4^3 + a2 4^2 +
- a1 4^1 == g[5],
- a8 5^8 + a7 5^7 + a6 5^6 + a5 5^5 + a4 5^4 + a3 5^3 + a2 5^2 +
- a1 5^1 == g[6],
- a8 6^8 + a7 6^7 + a6 6^6 + a5 6^5 + a4 6^4 + a3 6^3 + a2 6^2 +
- a1 6^1 == g[7],
- a8 7^8 + a7 7^7 + a6 7^6 + a5 7^5 + a4 7^4 + a3 7^3 + a2 7^2 +
- a1 7^1 == g[8],
- a8 8^8 + a7 8^7 + a6 8^6 + a5 8^5 + a4 8^4 + a3 8^3 + a2 8^2 +
- a1 8^1 == g[9]}, {a8, a7, a6, a5, a4, a3, a2, a1}, Integers];
- b = a[[1]];
- For[i = 1, i <= 8, i++,
- c[i] = b[[i]];
- ];
- Print["f(n)=",
- Factor[ c[1] n^8 + c[2] n^7 + c[3] n^6 + c[4] n^5 + c[5] n^4 +
- c[6] n^3 + c[7] n^2 + c[8] n]]
- f[n_] := Factor[
- c[1] n^8 + c[2] n^7 + c[3] n^6 + c[4] n^5 + c[5] n^4 + c[6] n^3 +
- c[7] n^2 + c[8] n]
- For[n = 1, n <= 19, n++,
- Print["m=", n + 1, "时,n=", n, ",f(", n, ")=", f[n]]
- ]
程序运行结果如下(注意,式中 n=m-1,所以当 m=3 时, n=2,f(n)=f(2) 即是用 3 种颜色时的涂色方法数。余类推):

|
|