mathematica 机器证明平面几何定理【例 1】

TSC999 · 发表于 2017-5-23 11:07:27

马上注册，结交更多好友，享用更多功能，让你轻松玩转社区。

您需要登录才可以下载或查看，没有账号？欢迎注册

×

李涛，张景中的高徒，专门研究机器证明。本人曾看过李涛多年前写的一篇论文。按此论文的思路，使用 mathematica 为平台，用机器证明的方法，试证了几个平面几何定理。
至于专用的机器证明软件，国内外应该都有，只是不容易下载得到。
本文的证明没有采用专用软件，通过阅读程序，也许可以有个机器证明的初步概念。

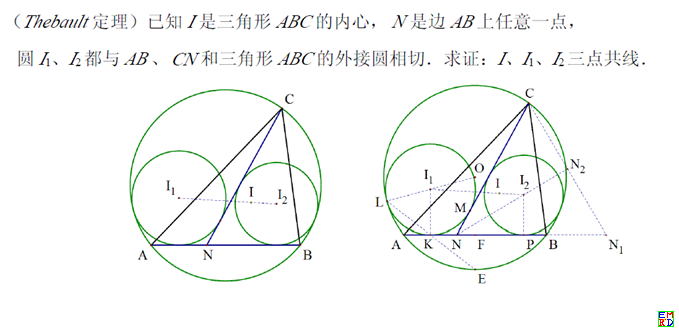
下面是编程证明平面几何中的泰博定理。

泰博定理图.png

u =.; v =.; a =.;
XI = 0; YI = 0; XA = u; YA = -1; XB = v; YB = -1;
ZA = XA + YA I; ZB = XB + YB I; ZI = XI + YI I;
XC =.; YC =.; aa = {XC, YC} /.
Solve[{(
XA Sqrt[(XB - XC)^2 + (YB - YC)^2] +
XB Sqrt[(XA - XC)^2 + (YA - YC)^2] +
XC Sqrt[(XA - XB)^2 + (YA - YB)^2])/(
Sqrt[(XA - XB)^2 + (YA - YB)^2] +
Sqrt[(XB - XC)^2 + (YB - YC)^2] +
Sqrt[(XC - XA)^2 + (YC - YA)^2]) == 0, (
YA Sqrt[(XB - XC)^2 + (YB - YC)^2] +
YB Sqrt[(XA - XC)^2 + (YA - YC)^2] +
YC Sqrt[(XA - XB)^2 + (YA - YB)^2])/(
Sqrt[(XA - XB)^2 + (YA - YB)^2] +
Sqrt[(XB - XC)^2 + (YB - YC)^2] +
Sqrt[(XC - XA)^2 + (YC - YA)^2]) == 0,
Abs[XA (YB - YC) + XB (YC - YA) + XC (YA - YB)]/(
Sqrt[(XA - XB)^2 + (YA - YB)^2] +
Sqrt[(XB - XC)^2 + (YB - YC)^2] +
Sqrt[(XC - XA)^2 + (YC - YA)^2]) == 1}, {XC, YC }];
bb = aa[[1]];
XC = bb[[1]];
YC = bb[[2]];
ZC = Simplify[XC + YC I];
Print["C = ", ZC]
(* 下面求三角形 ABC 外接圆圆心 O 的坐标及其半径 R *)
XO = ((XA^2 (YB - YC) + XB^2 ( YC - YA) +
XC^2 ( YA - YB)) - (YA - YB ) ( YB - YC) (YC - YA))/(
2 XA (YB - YC) + 2 XB ( YC - YA) + 2 XC ( YA - YB));
YO = -(((YA^2 (XB - XC) + YB^2 ( XC - XA) +
YC^2 ( XA - XB)) - (XA - XB ) ( XB - XC) (XC - XA))/(
2 XA (YB - YC) + 2 XB ( YC - YA) + 2 XC ( YA - YB)));
ZO = Factor[XO + YO I];
Print["O = ", ZO]
(* 下面求三角形 ABC 外接圆的半径 R *)
R = Assuming[u < 0 && v > 0 && 1 + u v < 0,
Factor[Simplify[
Sqrt[((XA - XB)^2 + (YA - YB)^2) ((XB - XC)^2 + (YB -
YC)^2) ((XC - XA)^2 + (YC - YA)^2)]/(
2 (XA (YB - YC) + XB (YC - YA) + XC (YA - YB)))]]];
Print["R = ", R];
(* 下面求 OF 线与 \[CircleDot]O 的交点 E 的坐标 *)
XE = Factor[ComplexExpand[Re[ZO]]];
YE = Factor[ComplexExpand[Im[ZO]] - R];
ZE = Simplify[XE + YE I];
Print["E = ", ZE]
ZF = (ZA + ZB)/2; (* F 是 AB 的中点 *)
ZK = Simplify[(1 - a) ZA +
a ZF] ; (* 在 AB 线上求一个 K 点，其位置由 a 决定。a 是介于 0 与 1 的实数。 *)
Print["K = ", ZK]
XK = Factor[ComplexExpand[Re[ZK]]];
YK = -1;
(* 下面求 EK 的延长线与 \[CircleDot]O 的交点 L 的坐标 *)
x =.; y =.; aa = {{x, y}} /.
Simplify[Assuming[u < 0 && v > 0 && 1 + u v < 0 && x < XK,
Solve[{(x - XK)/(y - YK) == (XK - XE)/(
YK - YE), (x - XO)^2 + (y - YO)^2 == R^2}, {Factor[
Simplify[x]], Factor[Simplify[y]] }]]];
bb = aa[[2]];(* 交点有两个，第一组解不符合要求，舍去。取第二组解 *)
cc = bb[[1]];
XL = cc[[1]];
YL = cc[[2]];
ZL = Simplify[XL + YL I] ;
Print["L = ", ZL]
(* 下面求 \[CircleDot]I1 圆心 I1 的复坐标，I1 点是 OL 线与通过 K 点的 AB 的垂线的交点 *)
(* x=XK 是通过 K 点的 AB 的垂线 KK1 的直线方程，KK1 与 OL 的交点即是 I1 点 *)
XL = Factor[ComplexExpand[Re[ZL]]];
YL = Factor[ComplexExpand[Im[ZL]]];
x =.; y =.; aa = {{x, y}} /.
Simplify[Solve[{(x - XO)/(y - YO) == (XO - XL)/(YO - YL),
x == XK}, {Factor[Simplify[x]], Factor[Simplify[y]] }]];
bb = aa[[1]];(* 交点只有一个，取第一组解 *)
cc = bb[[1]];
XI1 = cc[[1]];
YI1 = cc[[2]];
ZI1 = Simplify[Factor[XI1 + YI1 I] ];
Print["I1 = ", ZI1]
(* 从 C 点向 \[CircleDot]I1 作切线，切点为 M, 下面求 M 点的坐标 *)
x1 = XI1; y1 = YI1;(* 圆心坐标 *)
x2 = XC; y2 = YC; (* 向圆引切线的那个定点的坐标 *)
r = YI1 - YK; (* 左边 \[CircleDot]I1 圆的半径 *)
(* 所求的切点是 M1(XM1,YM1) 和 M2(XM2,YM2)，已知有以下公式： *)
XM1 = x1 - (
r^2 (x1 - x2) - (y1 - y2) r Sqrt[(x1 - x2)^2 + (y1 - y2)^2 -
r^2])/((x1 - x2)^2 + (y1 - y2)^2) ;
YM1 = y1 - (
r^2 (y1 - y2) + (x1 - x2) r Sqrt[(x1 - x2)^2 + (y1 - y2)^2 -
r^2])/((x1 - x2)^2 + (y1 - y2)^2) ;
(* 上面这个 ZM1 切点不符合要求，舍去 *)
XM2 = x1 - (
r^2 (x1 - x2) + (y1 - y2) r Sqrt[(x1 - x2)^2 + (y1 - y2)^2 -
r^2])/((x1 - x2)^2 + (y1 - y2)^2);
YM2 = y1 - (
r^2 (y1 - y2) - (x1 - x2) r Sqrt[(x1 - x2)^2 + (y1 - y2)^2 -
r^2])/((x1 - x2)^2 + (y1 - y2)^2);
ZM = Assuming[
1 + u v < 0 &&
1 > a > 0 && ((2 ((1 + u^2)) v + a ((u - v - u^2 v + u v^2)))) >
0, Simplify[Factor[XM2 + YM2 I]]];
(* 上面这条语句中，((2((1+u^2))v+a((u-v-u^2v+u v^2))))>0 \
这个条件是程序调试中发现的，不可能事先分析出来。若不加上这个条件，表达式就不能充分化简 *)
Print["M = ", ZM]
(* 将 CM 延长交 AB 于 N, 下面求 N 点的坐标 *)
XM = Factor[ComplexExpand[Re[ZM]]];
YM = Factor[ComplexExpand[Im[ZM]]];
x =.; y =.; aa = {{x, y}} /.
Simplify[Solve[{(x - XC)/(y - YC) == (XC - XM)/(YC - YM),
y == -1}, {Factor[Simplify[x]], Factor[Simplify[y]] }]];
bb = aa[[1]];(* 交点只有一个，取第一组解 *)
cc = bb[[1]];
XN = cc[[1]];
YN = cc[[2]];
ZN = Simplify[Factor[XN + YN I] ];
Print["N = ", ZN]
(* 延长 NB 到 N1, 使 NN1=NC *)
NC = Assuming[
u < 0 && v > 0 && 1 + u v < 0 && 1 > a > 0 && (-2 + a) u - a v < 0,
Simplify[Factor[Sqrt[(XN - XC)^2 + (YN - YC)^2]]]];
XN1 = Simplify[XN + NC];
ZN1 = Simplify[Factor[XN1 - 1 I] ];
Print["N1 = ", ZN1]
(* 求出 N1C 的中点 N2 *)
ZN2 = Simplify[Factor[(ZC + ZN1)/2]];
Print["N2 = ", ZN2]
(* 求出 NN2 与 I1I 的交点 I2, 此即 \[CircleDot]I2 的圆心 *)
XN2 = Factor[ComplexExpand[Re[ZN2]]];
YN2 = Factor[ComplexExpand[Im[ZN2]]];
x =.; y =.; aa = {{x, y}} /.
Simplify[Solve[{(x - XN2)/(y - YN2) == (XN2 - XN)/(YN2 - YN), (
x - XI)/(y - YI) == (XI - XI1)/(YI - YI1)}, {Factor[
Simplify[x]], Factor[Simplify[y]] }]];
bb = aa[[1]];(* 交点只有一个，取第一组解 *)
cc = bb[[1]];
XI2 = cc[[1]];
YI2 = cc[[2]];
ZI2 = Simplify[Factor[XI2 + YI2 I]];
Print["I2 = ", ZI2];
(* 求出 \[CircleDot]I2 圆的半径, 为此从 I2 点向 AB 作垂线, 垂足为 P, I2P 即是半径 *)
I2P = YI2 + 1;
R2 = I2P;
XP = XI2;
YP = -1;
ZP = Simplify[Factor[XP + YP I]];
Print["P = ", ZP];
(* 证明 \[CircleDot]I2 圆与 \[CircleDot]O 圆相切，就完成了全部证明。 *)
S = Assuming[
u < 0 && v > 0 && 1 + u v < 0 &&
1 - 2 (-2 + a) a u v + (-1 + a)^2 v^2 +
u^2 (1 - 2 a + a^2 + v^2) > 0,
Simplify[Sqrt[(XI2 - XO)^2 + (YI2 - YO)^2]]];
Print["S+R2 = ", Factor[Simplify[S + R2]]];
Print["R = ", R];
If[Factor[Simplify[S + R2]] == R, Print["由于 \!\(\*
StyleBox["S",\nFontColor->GrayLevel[0]]\)\!\(\*
StyleBox["+",\nFontColor->GrayLevel[0]]\)\!\(\*
StyleBox["R2",\nFontColor->GrayLevel[0]]\)\!\(\*
StyleBox["=",\nFontColor->GrayLevel[0]]\)R，因此 \[CircleDot]I2 圆与 \
\[CircleDot]O 圆相切。"]]

复制代码

程序运行结果：

上述运行结果，与李涛论文所给结果完全相同。李涛的结果是用他专门开发的机器证明软件做的，如果写出程序，必然是有许多子程序调用，因而程序看起来会简明得多。

TSC999 · 发表于 2017-5-23 11:24:47

我觉得机器证明中的一个最困难的环节，就是如何进行构图，使得每个关键点在复平面上的位置都能够用不太复杂的复数代数式来表达。如果公式过于复杂，mathematica 就不能胜任繁重的计算任务，即使经过长时间运行，也不能给出证明结果；或者即使能给出结果，但是需要时间过长，那就不是一个好的程序。

账号		自动登录	找回密码
密码			欢迎注册

[分享] mathematica 机器证明平面几何定理【例 1】

马上注册，结交更多好友，享用更多功能，让你轻松玩转社区。