三角形中三联等圆交于外心

hujunhua

hejoseph 发表于 2023-7-21 11:36
已知 △ABC 以及三个角α、β、γ，其中 α+β+γ=π，求作一点 P，使其到直线 BC、CA、AB 的垂足D、E、F满 ...

“作一个已知形状的三角形，使其顶点落在三条给定的直线上”比其对偶问题
“作一个已知形状的三角形，使其三边所在直线经过给定三点”
好像要麻烦一点。并且前者可以从后者得到解决。

TSC999

对于楼主首页问题，可用复平面解析方法证明，程序代码见
http://kuing.infinityfreeapp.com ... amp;extra=#pid55264

nyy

TSC999 发表于 2023-7-22 06:31
对于楼主首页问题，可用复平面解析方法证明，程序代码见
http://kuing.infinityfreeapp.com/forum.php?mod ...

http://kuing.infinityfreeapp.com ... 11171&pid=55264

20楼才是你的代码，我把20楼的精确链接给你复制过来了

hejoseph

作图问题是这样得到的：若点 \(D\)、\(E\)、\(F\) 分别在直线 \(BC\)、\(CA\)、\(AB\) 上，且 \(\triangle DEF\) 的三个内角是固定的已知值，\(\odot AEF\)、\(\odot BFD\)、\(\odot CDE\) 共点于 \(P\)，那么点 \(P\) 是一个定点，与点 \(D\)、\(E\)、\(F\) 的位置无关。若点 \(D\)、\(E\)、\(F\) 共线，那么点 \(P\) 必定在 \(\triangle ABC\) 的外接圆上，这也是 Simson 定理的逆定理。

lihpb00

这命题推广到四面体能成立吗？

wayne

为了让alphageometry也参与贡献。咱们翻译一下老胡的题目，先做一个圆$O$，在其上任取三点$O_1, O_2,O_3$,记三个圆两两相交的其他交点分别是$D,E,F$，也就是$O_1,O_2$交于$O,F$,$O_1,O_3$交于$O,E$,$O_2,O_3$交于$O,D$
设圆$O_1$上的自由点是$A$，那么$AF$交圆$O_2$于$B$,$AE$交圆$O_3$于$C$，那么就是要证明$B,D,C$共线，且$OA=OB=OC$。 geogebra按照上面的描述画的图

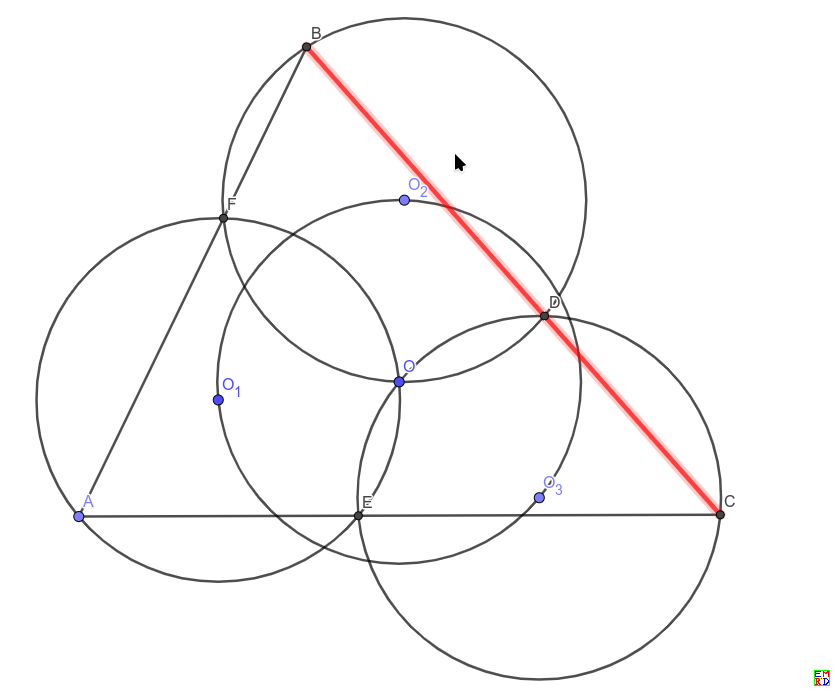
翻译成alphageometry的命题陈述的语法就是两个命题：

1. o = free; o1 = free; a = on_circle a o1 o; o2 = on_circle o2 o o1; f = on_circle f o1 o, on_circle f o2 o; o3 = on_circle o3 o o1; e = on_circle e o1 o, on_circle e o3 o; d = on_circle d o2 o, on_circle d o3 o; b = on_line b a f, on_circle b o2 o; c = on_line c a e, on_circle c o3 e ? coll b c d
   

复制代码

1. o = free; o1 = free; a = on_circle a o1 o; o2 = on_circle o2 o o1; f = on_circle f o1 o, on_circle f o2 o; o3 = on_circle o3 o o1; e = on_circle e o1 o, on_circle e o3 o; d = on_circle d o2 o, on_circle d o3 o; b = on_line b a f, on_circle b o2 o; c = on_line c a e, on_circle c o3 e ? cong o a o b o c
   

复制代码

然后输出的人类可读的证明如下：

证明输入的那个图里的$B,D,C$共线
alphageometry的输出图形把输入命题的点都重置了。重新标记了，如图：

1. 
   
2. ==========================
   
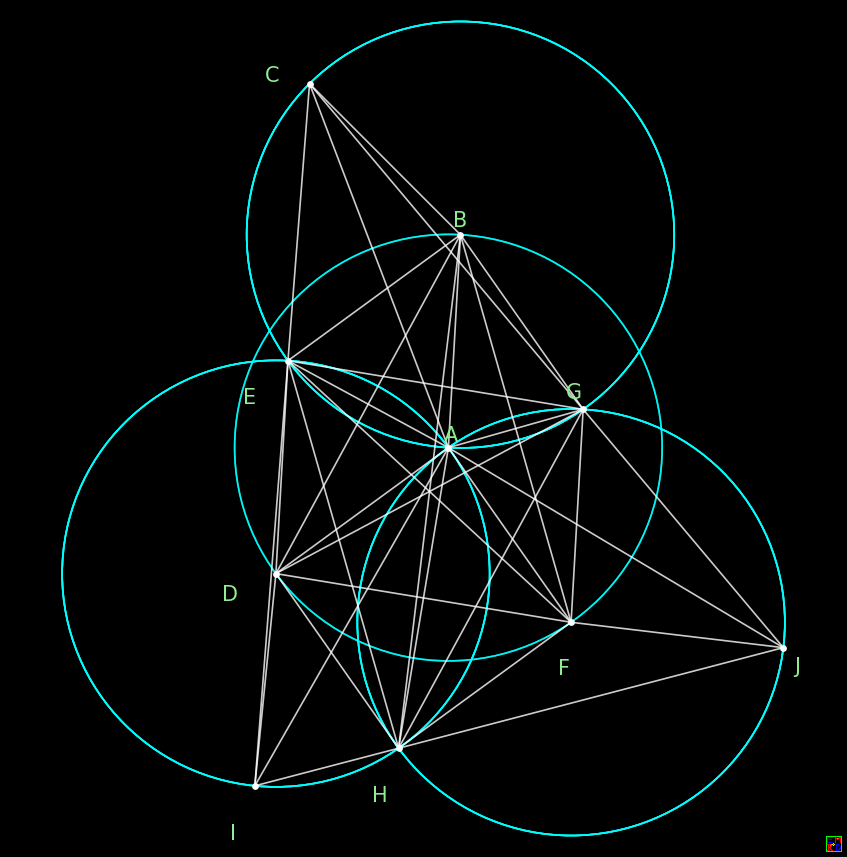
3. * From theorem premises:
   
4. A B C D E F G H I J : Points
   
5. BC = BA [00]
   
6. BE = BA [01]
   
7. DE = DA [02]
   
8. FG = FA [03]
   
9. BG = BA [04]
   
10. FH = FA [05]
    
11. DH = DA [06]
    
12. DI = DA [07]
    
13. I,C,E are collinear [08]
    
14. FJ = FG [09]
    
15. C,J,G are collinear [10]
    
16. 
    
17. * Auxiliary Constructions:
    
18. : Points
    
19. 
    
20. 
    
21. * Proof steps:
    
22. 001. FG = FA [03] & FJ = FG [09] & FH = FA [05] ⇒  H,A,J,G are concyclic [11]
    
23. 002. H,A,J,G are concyclic [11] ⇒  ∠HAG = ∠HJG [12]
    
24. 003. BC = BA [00] & BG = BA [04] & BE = BA [01] ⇒  A,C,E,G are concyclic [13]
    
25. 004. A,C,E,G are concyclic [13] ⇒  ∠CEA = ∠CGA [14]
    
26. 005. DE = DA [02] & DI = DA [07] & DH = DA [06] ⇒  H,A,I,E are concyclic [15]
    
27. 006. H,A,I,E are concyclic [15] ⇒  ∠HAE = ∠HIE [16]
    
28. 007. ∠HAG = ∠HJG [12] & C,J,G are collinear [10] & ∠CEA = ∠CGA [14] & ∠HAE = ∠HIE [16] & I,C,E are collinear [08] ⇒  ∠IHA = ∠JHA [17]
    
29. 008. ∠IHA = ∠JHA [17] ⇒  HI ∥ HJ [18]
    
30. 009. HI ∥ HJ [18] ⇒  H,I,J are collinear
    
31. ==========================
    

复制代码

再让他证明输入图的$OA = OB$，如下(alphageometry的输出图形把输入命题的点都重置了。重新标记了)

1. ==========================
   
2. * From theorem premises:
   
3. A B C D E I : Points
   
4. BC = BA [00]
   
5. AD = AB [01]
   
6. DE = DA [02]
   
7. BE = BA [03]
   
8. I,E,C are collinear [04]
   
9. DI = DA [05]
   
10. 
    
11. * Auxiliary Constructions:
    
12. F G H : Points
    
13. AF = AB [06]
    
14. BG = BA [07]
    
15. FG = FA [08]
    
16. DH = DA [09]
    
17. FH = FA [10]
    
18. 
    
19. * Proof steps:
    
20. 001. BG = BA [07] & AF = AB [06] & FG = FA [08] ⇒  GF = GB [11]
    
21. 002. AF = AB [06] & GF = GB [11] ⇒  BF ⟂ AG [12]
    
22. 003. AF = AB [06] & AD = AB [01] ⇒  AD = AF [13]
    
23. 004. DH = DA [09] & AD = AB [01] & AF = AB [06] & FH = FA [10] ⇒  HF = HD [14]
    
24. 005. AD = AF [13] & HF = HD [14] ⇒  DF ⟂ AH [15]
    
25. 006. BF ⟂ AG [12] & DF ⟂ AH [15] ⇒  ∠(BF-AG) = ∠(AH-DF) [16]
    
26. 007. FG = FA [08] & AF = AB [06] ⇒  AB = GF [17]
    
27. 008. AD = AB [01] & DE = DA [02] ⇒  AB = ED [18]
    
28. 009. AB = GF [17] & AB = ED [18] ⇒  DE = GF [19]
    
29. 010. BG = BA [07] & AF = AB [06] ⇒  FA = BG [20]
    
30. 011. AB = GF [17] & FA = BG [20] (SSS)⇒  AB ∥ FG [21]
    
31. 012. BE = BA [03] & AD = AB [01] ⇒  AD = EB [22]
    
32. 013. DE = BA [18] & AD = EB [22] (SSS)⇒  DE ∥ AB [23]
    
33. 014. AB ∥ FG [21] & DE ∥ AB [23] ⇒  ∠DEF = ∠GFE [24]
    
34. 015. DE = GF [19] & ∠DEF = ∠GFE [24] (SAS)⇒  ∠(DE-FG) = ∠(DF-EG) [25]
    
35. 016. ∠(BF-AG) = ∠(AH-DF) [16] & ∠(DE-FG) = ∠(DF-EG) [25] & AB ∥ FG [21] & DE ∥ AB [23] ⇒  ∠(FB-AG) = ∠(AH-GE) [26]
    
36. 017. DH = DA [09] & DI = DA [05] & DE = DA [02] ⇒  H,A,E,I are concyclic [27]
    
37. 018. H,A,E,I are concyclic [27] ⇒  ∠HAI = ∠HEI [28]
    
38. 019. DH = DA [09] & AD = AB [01] & AF = AB [06] ⇒  AF = HD [29]
    
39. 020. FH = FA [10] & AF = AB [06] & AD = AB [01] ⇒  DA = FH [30]
    
40. 021. DA = FH [30] & AF = HD [29] (SSS)⇒  AF ∥ DH [31]
    
41. 022. AF ∥ DH [31] & DE ∥ AB [23] ⇒  ∠EDH = ∠BAF [32]
    
42. 023. DE = BA [18] & AF = HD [29] & ∠EDH = ∠BAF [32] (SAS)⇒  ∠(DE-AB) = ∠(EH-BF) [33]
    
43. 024. I,E,C are collinear [04] & ∠HAI = ∠HEI [28] & ∠(DE-AB) = ∠(EH-BF) [33] & DE ∥ AB [23] ⇒  ∠HAI = ∠(FB-IE) [34]
    
44. 025. ∠(FB-AG) = ∠(AH-GE) [26] & ∠HAI = ∠(FB-IE) [34] ⇒  ∠(GE-IA) = ∠(AG-IE) [35]
    
45. 026. BE = BA [03] & BG = BA [07] & BC = BA [00] ⇒  A,E,G,C are concyclic [36]
    
46. 027. A,E,G,C are concyclic [36] ⇒  ∠AGE = ∠ACE [37]
    
47. 028. I,E,C are collinear [04] & ∠(GE-IA) = ∠(AG-IE) [35] & ∠AGE = ∠ACE [37] ⇒  ∠ACI = ∠CIA [38]
    
48. 029. ∠ACI = ∠CIA [38] ⇒  AC = AI
    
49. ==========================
    

复制代码