- 注册时间
- 2009-6-9
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 19997
- 在线时间
- 小时
|
 发表于 2021-6-1 22:11:10
|
显示全部楼层
发表于 2021-6-1 22:11:10
|
显示全部楼层
对于三角形\(ABC\)的内心\(I\)将原三角形分成6个三角形\(AIE,AIF,BIF,BID,BID,CID,CIE\),(其中\(D,E,F\)分别为\(AI,BI,CI\)延长线交对边的点)且这6个小三角形的内心分别设为\(I1,I2,I3,I4,I5,I6\)
为了便于分析与计算,我们将\(B\)点设为原点\(O,C\)点位于\(X\)正半轴上,并设
\(A[x1,y1],B[x2,y2],C[x3,y3],D[x11,y11],E[x12,y12],F[x13,y13],I[x0,y0],I1[x21,y21],I2[x22,y22],I3[x23,y23],I4[x24,y24],I5[x25,y25],I6[x26,y26]\)
\(AB=c,AC=b,BC=a,AD=t1,BE=t2,CF=t3,BD=a11,DC=a12,CE=b11,AE=b12,AF=c11,BF=c12\)
我们可以得到:
\(x1=\frac{a^2-b^2+c^2}{2a},y1=\frac{2s}{a},x2=0,y2=0,x3=a,y3=0,x0=\frac{a-b+c}{2},y0=\frac{2s}{a+b+c},x11=\frac{ac}{b+c},y11=0,x12=\frac{(a+c)^2-b^2}{2(a+c)},y12=\frac{2s}{a+c}
x13=\frac{a^2-b^2+c^2}{2(a+b)},y13=\frac{2s}{a+b}\)
\(a11=\frac{ac}{b+c},a12=\frac{ab}{b+c},b11=\frac{ab}{a+c},b12=\frac{bc}{a+c},c11=\frac{bc}{a+b},c12=\frac{ac}{a+b},a1=\frac{t1(b+c)}{a+b+c},a2=\frac{at1}{a+b+c},b1=\frac{(a+c)t2}{a+b+c},
b2=\frac{bt2}{a+b+c},c1=\frac{(a+b)t3}{a+b+c},c2=\frac{ct3}{a+b+c}\)
\(x21=\frac{a1x12 + b12x0 + b2x1}{b2 + b12 + a1}, y21=\frac{a1y12 + b12y0 + b2y1}{b2 + b12 + a1}, x22=\frac{a1x13 + c11x0 + c2x1}{c2 + c11 + a1}, y22=\frac{a1y13 + c11y0 + c2y1}{c2 + c11 + a1}, x23=\frac{b1x13 + c12x0 + c2x2}{c2 + c12 + b1}, y23=\frac{b1y13 + c12y0 + c2y2}{c2 + c12 + b1}
, x24=\frac{a11x0 + a2x2 + b1x11}{a2 + a11 + b1}, y24 =\frac{a11y0 + a2y2 + b1y11}{a2 + a11 + b1}, x25=\frac{a12x0 + a2x3 + c1x11}{a2 + a12 + c1}, y25=\frac{a12y0 + a2y3 + c1y11}{a2 + a12 + c1}, x26=\frac{b11x0 + b2x3 + c1x12}{b2 + b11 + c1}, y26=\frac{b11y0 + b2y3 + c1y12}{b2 + b11 + c1}\)
\(t1=\frac{\sqrt{bc(a+b+c)(-a+b+c)}}{b+c},t2=\frac{\sqrt{ac(a+b+c)(a-b+c)}}{a+c},t3=\frac{\sqrt{ab(a+b+c)(a+b-c)}}{a+b},s=\frac{\sqrt{2a^2b^2+2a^2c^2+2b^2c^2-a^4-b^4-c^4}}{4}\)
\(I1,I2,I3,I4,I5,I6\)选较简单的后5个点坐标构成椭圆曲线
\[\det{\left(
\begin{array}{cccccc}
x^2& xy& y^2& x&y,&1\\
x22^2&x22y22&y22^2&x22&y22&1\\
x23^2&x23y23&y23^2&x23&y23&1\\
x24^2&x24y24&y24^2&x24&y24&1\\
x25^2&x25y25&y25^2&x25&y25&1\\
x26^2&x26y26&y26^2&x26&y26&1\\
\end{array}
\right) }=0\]
例如:取\({a=5,b=4,c=3}\)
得到
\(a = 5, a1=\sqrt{2}, a11 = \frac{15}{7}, a12 =\frac{20}{7}, a2 = \frac{5\sqrt{2}}{7}, b = 4, b1 = \sqrt{5}, b11=\frac{5}{2}, b12=\frac{3}{2}, b2=\frac{\sqrt{5}}{2}, c = 3, c1 =\sqrt{10}, c11=\frac{4}{3}, c12=\frac{5}{3}, c2 =\sqrt{10}{3}, s = 6, t1=\frac{12\sqrt{2}}{7}, t2=\frac{3\sqrt{5}}{2}, t3=\frac{4\sqrt{10}}{3}, x0 = 2, x1 =\frac{9}{5}, x11=\frac{15}{7}, x12 = 3, x13 = 1, x2 = 0, x3 = 5, y0 = 1, y1=\frac{12}{5}, y11 = 0, y12 =\frac{3}{2}, y13 =\frac{4}{3}, y2 = 0, y3 = 0\)
\(x21 =\frac{2880 + 2880\sqrt{2}+ 864\sqrt{5}}{10(144 + 96\sqrt{2}+ 48\sqrt{5})}, x22 =\frac{2880 + 1080\sqrt{2}+ 648\sqrt{10}}{10(144 + 108\sqrt{2}+ 36\sqrt{10})}, x23 =\frac{720 + 216\sqrt{5}}{2(180 + 108\sqrt{5}+ 36\sqrt{10})}, x24 = \frac{15(48 + 24\sqrt{5})}{2(180 + 60\sqrt{2}+ 84\sqrt{5})}, x25 =\frac{5(192 + 120\sqrt{2}+ 72\sqrt{10})}{2(240 + 60\sqrt{2}+ 84\sqrt{10})}, x26 =\frac{960 + 576\sqrt{10}+ 480\sqrt{5}}{2(240 + 96\sqrt{10} + 48\sqrt{5})}, y21 = \frac{12(60 + 60\sqrt{2}+ 48\sqrt{5}}{5(144 + 96\sqrt{2}+ 48\sqrt{5})}, y22 =\frac{12(60 + 60\sqrt{2}+ 36\sqrt{10})}{5(144 + 108\sqrt{2}+ 36\sqrt{10})}, y23 = \frac{12(15 + 12\sqrt{5})}{180 + 108\sqrt{5} + 36\sqrt{10}}, y24 =\frac{180}{180 + 60\sqrt{2}+ 84\sqrt{5}}, y25 = \frac{240}{240 + 60\sqrt{2}+ 84\sqrt{10}}, y26 =\frac{12(20 + 12\sqrt{10})}{240 + 96\sqrt{10}+ 48\sqrt{5}}\)
椭圆曲线方程:
\((465865600000\sqrt{10}+ 657851200000\sqrt{5}+ 1038608000000\sqrt{2}+ 1477336000000)x^2 + ((43001600000\sqrt{10}+ 97088000000\sqrt{2}+ 63683200000\sqrt{5}+ 136976000000)y - 1952544000000\sqrt{10} - 4351680000000\sqrt{2}- 2757312000000\sqrt{5} - 6189600000000)x + (1024374400000\sqrt{10}+ 2294192000000\sqrt{2}+ 1448708800000\sqrt{5}+ 3245704000000)y^2 + (-2063712000000\sqrt{10}- 4633440000000\sqrt{2}- 2924256000000\sqrt{5}- 6549600000000)y + 8231400000000 + 5799600000000\sqrt{2}+ 2597040000000\sqrt{10} + 3668760000000\sqrt{5}=0\)
若消元可以得到:(一般表达式见附件,只含\(a,b,c,x,y\))
F1: \(121186279x^8 - 168512396x^7y - 108228692x^6y^2 - 65161548x^5y^3 - 402431070x^4y^4 + 131013868x^3y^5 - 82188452x^2y^6 + 7291116xy^7 + 21119y^8 - 2264732500x^7 + 2182105400x^6y + 1544825300x^5y^2 - 917671000x^4y^3 + 3749646500x^3y^4 - 1667779000x^2y^5 + 425714300xy^6 - 16143400y^7 + 16821693700x^6 - 9733579100x^5y - 8472300500x^4y^2 + 10502577000x^3y^3 - 14462454500x^2y^4 + 5397472900xy^5 - 542302700y^6 - 63619801500x^5 + 17096885000x^4y + 23690115000x^3y^2 - 31225170000x^2y^3 + 25547692500xy^4 - 5204323000y^5 + 127737391250x^4 - 2691082500x^3y - 22808947500x^2y^2 + 31330282500xy^3 - 16654783750y^4 - 118412287500x^3 - 16203975000x^2y - 28204387500xy^2 - 4653675000y^3 + 3679312500x^2 - 16931812500xy + 51136312500y^2 + 68588437500x + 39639375000y - 30406640625=0\)
F2: \(41659039x^8 - 69730684x^7y + 286833508x^6y^2 - 37209612x^5y^3 + 386084730x^4y^4 + 219518012x^3y^5 - 146455292x^2y^6 - 15692916xy^7 + 11868239y^8 - 601730380x^7 - 72003080x^6y - 3572639620x^5y^2 - 2078162600x^4y^3 - 4549171300x^3y^4 - 59095640x^2y^5 + 610175060xy^6 + 7908040y^7 + 4063741900x^6 + 7154965700x^5y + 22172801500x^4y^2 + 21578181000x^3y^3 + 13495178500x^2y^4 - 2238922300xy^5 - 889337900y^6 - 17105332500x^5 - 48172625000x^4y - 83709675000x^3y^2 - 67073850000x^2y^3 - 11779462500xy^4 + 3633115000y^5 + 48826666250x^4 + 150796807500x^3y + 176933227500x^2y^2 + 77586142500xy^3 + 688216250y^4 - 94309912500x^3 - 252919275000x^2y - 180009262500xy^2 - 29643825000y^3 + 116389687500x^2 + 215322187500xy + 68470312500y^2 - 81042187500x - 72309375000y + 23762109375=0\)
画图得到:
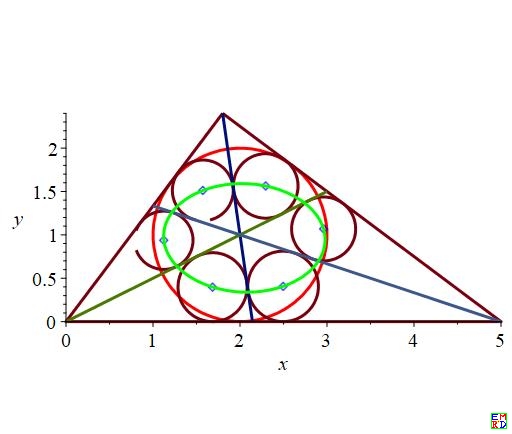
绿色曲线为F2,其中有部分与红色椭圆曲线重合
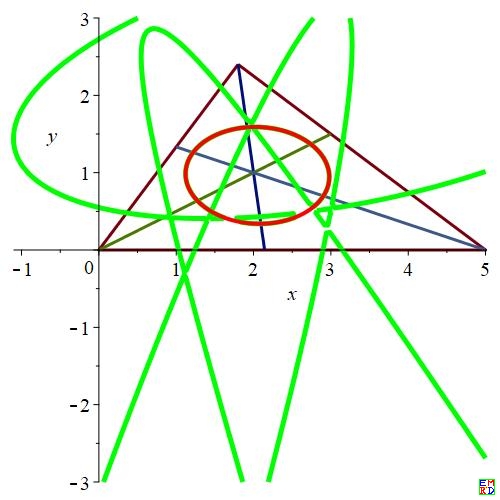
|
-

-
三角形6内心曲线.rar
1014.51 KB, 下载次数: 2, 下载积分: 金币 -1 枚, 经验 1 点, 下载 1 次
|