非随机正方形连棋

KeyTo9_Fans

这个游戏改编自《随机正方形连棋》：

https://bbs.emath.ac.cn/thread-1819-1-1.html

不同之处用红色标出了：

=======================
两人在$n*n$的正方形棋盘里下子。

双方的胜利条件都是将棋盘的对边用自己的棋子连起来。

其中一方连接上下两条边，棋子是四连通的（可以往上下左右四个方向相连），下图是四连通赢的一个例子：



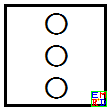
另一方连接左右两条边，棋子是八连通的（不仅上下左右，还可以往对角方向相连），下图是八连通赢的一个例子：



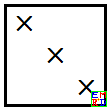
每一步轮到谁下是完全确定的，具体规则如下：

八连通方每次只能下一个棋子，而四连通方有时可以一次下多个棋子，

双方的下子序列在任何时候都满足：

四连通方所下的棋子数所占的比例是最接近$p$的分数，$p$是游戏开始前双方约定好的一个大于$1/2$的常数。

例如，当$p=2/3$时，双方的下子序列如下：

○×○ ○×○ ○×○ ○×○ ○×○ ......
=======================

我们可以这样说：

$p$越大表明四连通方下子的机会越多，四连通方越容易赢；

$p$越小表明四连通方下子的机会越少，八连通方越容易赢。

链接里的《随机正方形连棋》每一步都需要抛硬币决定谁下（硬币抛出四连通方的概率$p$比八连通方的概率$(1-p)$大），输赢有很大的运气成分。

而本贴的非随机正方形连棋则完全不需要抛硬币，没有运气成分了，输赢全凭实力。

我们要解决的问题是：

当$p$的值取多少时，恰好是四连通方必胜与八连通方必胜的分界线？

#####

目前我已经证出$p=1/2$时，八连通方必胜；$p=2/3$时，四连通方必胜。

剩下的问题就是要在$(1/2,2/3)$区间里，找到更精准的分界线$p$。

当$n=1,2,3,4,5$时，准确的分界线$p$的值如下：

$1/2, 3/5, 4/7, 7/12, 11/19$。

当$n=6$时，单机单线程算了一个多月，还没算出最终结果。

根据已有的结果，我有较大的把握，认为这个分界线$p$是严格比《随机正方形连棋》的公平$p$值要小的。

例如，当$n=15$时，《随机正方形连棋》的公平$p$值约为$0.59$：



但是非随机正方形连棋的$p$值即使只取$0.58$，对四连通方来说，也是太容易赢了。

为了验证上面这个论断，我编写了下面这个游戏：

P_Turn_Square.zip (124.06 KB, 下载次数: 2)

2021-7-20 17:03 上传

点击文件名下载附件

下载附件，解压后就可以玩了。

电脑为四连通方，玩家为八连通方，$n$为$15$，$p$为$0.58$。

我玩下来的结果是一把都赢不了，如下图所示：



坛友们不妨也试玩一下，看看是不是也赢不了电脑。

如果赢不了，那么我猜测当n→∞时，双方输赢分界线$p(n)$的极限值只有$0.57$左右（那时候我会把附件里的参数改成$p=0.57$，让大家继续测试），

这个值是严格小于《随机正方形连棋》的公平$p$值的极限值$0.59274605079$的。

#####

如果对这个游戏感兴趣的坛友较多，我打算建一个群（目前可以申请进入这个临时的QQ群，群号是6807814），

然后群友们通过实战（双人对战、人机对战或AI对战），

来找到较为准确的公平$p$值。

如果人不多就算了，还是由我一个人继续研究这个问题。

KeyTo9_Fans

呃……电脑有时候会犯傻，然后就被玩家钻空子赢了……



看来这个电脑下棋的程序还得加强。