史勇的一个经典几何案例

dlsh

乘积与线段平方的差

markfang2050

凡是以自己名字标榜的所谓定理发现，都是“妄人”。整天搞这些初等数学题，真想不通不是在浪费生命？真有能力，真知灼见，还是发表论文或搞一些应用项目也好。对国家社会个人也是好事。

TSC999

史勇不知是何方大侠？ 他有一套奇特的对合理论，对于平面几何图形的构图方法有独到研究。他在机器证明中好像很少用到共轭复数。

彭翕成

很难想象这里的E，F，坐标能很简单的求出来

dlsh

1. Clear["Global`*"]
   
2. 
   
3. \!\(\*OverscriptBox["o", "_"]\) = o = 0;
   
4. \!\(\*OverscriptBox["a", "_"]\) = 1/a;
   
5. \!\(\*OverscriptBox["b", "_"]\) = 1/b; b = -I/v; c = -
   
6. \!\(\*OverscriptBox["b", "_"]\);
   
7. \!\(\*OverscriptBox["c", "_"]\) = 1/c;(*圆心在原点，假设e^(i\[Alpha])=v*)
   
8. m = (b + c)/2;
   
9. \!\(\*OverscriptBox["m", "_"]\) = (
   
10. \!\(\*OverscriptBox["b", "_"]\) +
    
11. \!\(\*OverscriptBox["c", "_"]\))/2; h = a + b + c;
    
12. \!\(\*OverscriptBox["h", "_"]\) =
    
13. \!\(\*OverscriptBox["a", "_"]\) +
    
14. \!\(\*OverscriptBox["b", "_"]\) +
    
15. \!\(\*OverscriptBox["c", "_"]\);(*外心在原点成立*)
    
16. k[a_, b_] := (a - b)/(
    
17. \!\(\*OverscriptBox["a", "_"]\) -
    
18. \!\(\*OverscriptBox["b", "_"]\));
    
19. \!\(\*OverscriptBox["k", "_"]\)[a_, b_] := 1/k[a, b];(*复斜率定义*)
    
20. 
    
21. e = a ((a - c) (
    
22. \!\(\*OverscriptBox["a", "_"]\) -
    
23. \!\(\*OverscriptBox["c", "_"]\)) - (b - c) (
    
24. \!\(\*OverscriptBox["b", "_"]\) -
    
25. \!\(\*OverscriptBox["c", "_"]\)) )/(b - a) + b; f = a ((a - b) (
    
26. \!\(\*OverscriptBox["a", "_"]\) -
    
27. \!\(\*OverscriptBox["b", "_"]\)) - (b - c) (
    
28. \!\(\*OverscriptBox["b", "_"]\) -
    
29. \!\(\*OverscriptBox["c", "_"]\)))/(a - c) + c;(*把
    
30. \!\(\*OverscriptBox["BA", "\[RightVector]"]\)和
    
31. \!\(\*OverscriptBox["BE", "\[RightVector]"]\)旋转到
    
32. \!\(\*OverscriptBox["AC", "\[RightVector]"]\)相同的方向，再利用复斜率，根据线段相等条件求得*)
    
33. 
    
34. \!\(\*OverscriptBox["e", "_"]\) =
    
35. \!\(\*OverscriptBox["a", "_"]\) ((a - c) (
    
36. \!\(\*OverscriptBox["a", "_"]\) -
    
37. \!\(\*OverscriptBox["c", "_"]\)) - (b - c) (
    
38. \!\(\*OverscriptBox["b", "_"]\) -
    
39. \!\(\*OverscriptBox["c", "_"]\)))/(
    
40. \!\(\*OverscriptBox["b", "_"]\) -
    
41. \!\(\*OverscriptBox["a", "_"]\)) +
    
42. \!\(\*OverscriptBox["b", "_"]\);
    
43. \!\(\*OverscriptBox["f", "_"]\) =
    
44. \!\(\*OverscriptBox["a", "_"]\) ((a - b) (
    
45. \!\(\*OverscriptBox["a", "_"]\) -
    
46. \!\(\*OverscriptBox["b", "_"]\)) - (b - c) (
    
47. \!\(\*OverscriptBox["b", "_"]\) -
    
48. \!\(\*OverscriptBox["c", "_"]\)))/(
    
49. \!\(\*OverscriptBox["a", "_"]\) -
    
50. \!\(\*OverscriptBox["c", "_"]\)) +
    
51. \!\(\*OverscriptBox["c", "_"]\);
    
52. n = (e + f)/2;
    
53. \!\(\*OverscriptBox["n", "_"]\) = (
    
54. \!\(\*OverscriptBox["e", "_"]\) +
    
55. \!\(\*OverscriptBox["f", "_"]\))/2;
    
56. Simplify[{b,
    
57. \!\(\*OverscriptBox["b", "_"]\), c,
    
58. \!\(\*OverscriptBox["c", "_"]\), , e,
    
59. \!\(\*OverscriptBox["e", "_"]\), f,
    
60. \!\(\*OverscriptBox["f", "_"]\)}]
    
61. Simplify[{h, m, n, k[o, h], k[m, n], , (h - o)/(m - n), (
    
62. \!\(\*OverscriptBox["h", "_"]\) -
    
63. \!\(\*OverscriptBox["o", "_"]\))/(
    
64. \!\(\*OverscriptBox["m", "_"]\) -
    
65. \!\(\*OverscriptBox["n", "_"]\))}]

复制代码

1. 
   
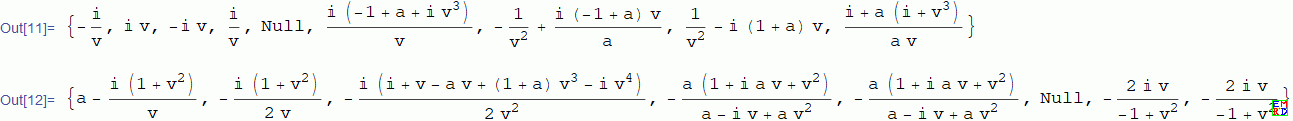
2. \!\(\*OverscriptBox["b", "_"]\) = b = 0;
   
3. \!\(\*OverscriptBox["c", "_"]\) = c = 1; a = 1/(1 - \[Lambda] v);
   
4. \!\(\*OverscriptBox["a", "_"]\) = v/(v - \[Lambda]);(*假设
   
5. \!\(\*OverscriptBox["AC", "\[RightVector]"]\)/
   
6. \!\(\*OverscriptBox["AB", "\[RightVector]"]\)=\[Lambda]v*)
   
7. m = (b + c)/2;
   
8. \!\(\*OverscriptBox["m", "_"]\) = (
   
9. \!\(\*OverscriptBox["b", "_"]\) +
   
10. \!\(\*OverscriptBox["c", "_"]\))/2; n = (e + f)/2;
    
11. \!\(\*OverscriptBox["n", "_"]\) = (
    
12. \!\(\*OverscriptBox["e", "_"]\) +
    
13. \!\(\*OverscriptBox["f", "_"]\))/2;
    
14. k[a_, b_] := (a - b)/(
    
15. \!\(\*OverscriptBox["a", "_"]\) -
    
16. \!\(\*OverscriptBox["b", "_"]\));
    
17. \!\(\*OverscriptBox["k", "_"]\)[a_, b_] := 1/k[a, b];(*复斜率定义*)
    
18. kAB = k[a, b]; kAC = k[a, c];
    
19. Chuixin[a_, b_, c_] := (
    
20. \!\(\*OverscriptBox["a", "_"]\) (b - c) (b + c - a) +
    
21. \!\(\*OverscriptBox["b", "_"]\) (c - a) (c + a - b) +
    
22. \!\(\*OverscriptBox["c", "_"]\) (a - b) (a + b - c) )/((b - c)
    
23. \!\(\*OverscriptBox["a", "_"]\) + (-a + c)
    
24. \!\(\*OverscriptBox["b", "_"]\) + (a - b)
    
25. \!\(\*OverscriptBox["c", "_"]\));(*垂心公式*)
    
26. 
    
27. \!\(\*OverscriptBox["Chuixin", "_"]\)[a_, b_, c_] := -((a (
    
28. \!\(\*OverscriptBox["b", "_"]\) -
    
29. \!\(\*OverscriptBox["c", "_"]\)) (
    
30. \!\(\*OverscriptBox["b", "_"]\) +
    
31. \!\(\*OverscriptBox["c", "_"]\) -
    
32. \!\(\*OverscriptBox["a", "_"]\)) + b (
    
33. \!\(\*OverscriptBox["c", "_"]\) -
    
34. \!\(\*OverscriptBox["a", "_"]\)) (
    
35. \!\(\*OverscriptBox["c", "_"]\) +
    
36. \!\(\*OverscriptBox["a", "_"]\) -
    
37. \!\(\*OverscriptBox["b", "_"]\)) + c (
    
38. \!\(\*OverscriptBox["a", "_"]\) -
    
39. \!\(\*OverscriptBox["b", "_"]\)) (
    
40. \!\(\*OverscriptBox["a", "_"]\) +
    
41. \!\(\*OverscriptBox["b", "_"]\) -
    
42. \!\(\*OverscriptBox["c", "_"]\)) )/((b - c)
    
43. \!\(\*OverscriptBox["a", "_"]\) + (-a + c)
    
44. \!\(\*OverscriptBox["b", "_"]\) + (a - b)
    
45. \!\(\*OverscriptBox["c", "_"]\)));
    
46. Waixin[a_, b_, c_] := (a
    
47. \!\(\*OverscriptBox["a", "_"]\) (b - c) + b
    
48. \!\(\*OverscriptBox["b", "_"]\) (c - a) + c
    
49. \!\(\*OverscriptBox["c", "_"]\) (a - b) )/(
    
50. \!\(\*OverscriptBox["a", "_"]\) (b - c) +
    
51. \!\(\*OverscriptBox["b", "_"]\) (c - a) +
    
52. \!\(\*OverscriptBox["c", "_"]\) (a - b));
    
53. \!\(\*OverscriptBox["Waixin", "_"]\)[a_, b_, c_] := -((a
    
54. \!\(\*OverscriptBox["a", "_"]\) (
    
55. \!\(\*OverscriptBox["b", "_"]\) -
    
56. \!\(\*OverscriptBox["c", "_"]\)) + b
    
57. \!\(\*OverscriptBox["b", "_"]\) (
    
58. \!\(\*OverscriptBox["c", "_"]\) -
    
59. \!\(\*OverscriptBox["a", "_"]\)) + c
    
60. \!\(\*OverscriptBox["c", "_"]\) (
    
61. \!\(\*OverscriptBox["a", "_"]\) -
    
62. \!\(\*OverscriptBox["b", "_"]\)) )/(
    
63. \!\(\*OverscriptBox["a", "_"]\) (b - c) +
    
64. \!\(\*OverscriptBox["b", "_"]\) (c - a) +
    
65. \!\(\*OverscriptBox["c", "_"]\) (a - b)));(*外心公式*)
    
66. 
    
67. h = Chuixin[a, b, c];
    
68. \!\(\*OverscriptBox["h", "_"]\) =
    
69. \!\(\*OverscriptBox["Chuixin", "_"]\)[a, b, c]; o = Waixin[a, b, c];
    
70. \!\(\*OverscriptBox["o", "_"]\) =
    
71. \!\(\*OverscriptBox["Waixin", "_"]\)[a, b, c];
    
72. 
    
73. e = kAC ((a - c) (
    
74. \!\(\*OverscriptBox["a", "_"]\) -
    
75. \!\(\*OverscriptBox["c", "_"]\)) - (b - c) (
    
76. \!\(\*OverscriptBox["b", "_"]\) -
    
77. \!\(\*OverscriptBox["c", "_"]\)) )/((b - a) I v) + b; f =
    
78. v kAB ((a - b) (
    
79. \!\(\*OverscriptBox["a", "_"]\) -
    
80. \!\(\*OverscriptBox["b", "_"]\)) - (b - c) (
    
81. \!\(\*OverscriptBox["b", "_"]\) -
    
82. \!\(\*OverscriptBox["c", "_"]\)))/(I (a - c)) + c;(*把
    
83. \!\(\*OverscriptBox["BA", "\[RightVector]"]\)和
    
84. \!\(\*OverscriptBox["BE", "\[RightVector]"]\)旋转到
    
85. \!\(\*OverscriptBox["AC", "\[RightVector]"]\)相同的方向，再利用复斜率，根据线段相等条件求得*)
    
86. 
    
87. \!\(\*OverscriptBox["e", "_"]\) = v ((a - c) (
    
88. \!\(\*OverscriptBox["a", "_"]\) -
    
89. \!\(\*OverscriptBox["c", "_"]\)) - (b - c) (
    
90. \!\(\*OverscriptBox["b", "_"]\) -
    
91. \!\(\*OverscriptBox["c", "_"]\)))/(-I (
    
92. \!\(\*OverscriptBox["b", "_"]\) -
    
93. \!\(\*OverscriptBox["a", "_"]\)) kAC) +
    
94. \!\(\*OverscriptBox["b", "_"]\);
    
95. \!\(\*OverscriptBox["f", "_"]\) = ((a - b) (
    
96. \!\(\*OverscriptBox["a", "_"]\) -
    
97. \!\(\*OverscriptBox["b", "_"]\)) - (b - c) (
    
98. \!\(\*OverscriptBox["b", "_"]\) -
    
99. \!\(\*OverscriptBox["c", "_"]\)))/(-I (
    
100. \!\(\*OverscriptBox["a", "_"]\) -
     
101. \!\(\*OverscriptBox["c", "_"]\)) v kAB) +
     
102. \!\(\*OverscriptBox["c", "_"]\);
     
103. 
     
104. Simplify[{e,
     
105. \!\(\*OverscriptBox["e", "_"]\), f,
     
106. \!\(\*OverscriptBox["f", "_"]\)}]
     
107. Simplify[{h,
     
108. \!\(\*OverscriptBox["h", "_"]\), o,
     
109. \!\(\*OverscriptBox["o", "_"]\), , m,
     
110. \!\(\*OverscriptBox["m", "_"]\), n,
     
111. \!\(\*OverscriptBox["n", "_"]\), , k[o, h], k[m, n]}]
     
112. Simplify[{(h - o)/(n - m)}]

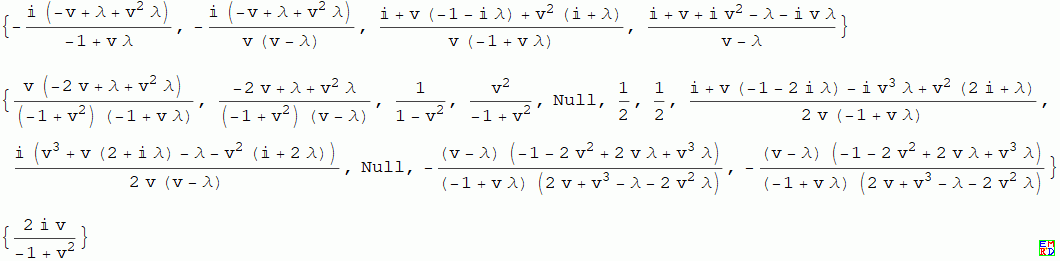
复制代码

dlsh

\(设B在原点，c=1,e^{i\alpha}=u{,}e^{i\beta}=v{,}\)，染色部分的几何意义如图中的数据，这种构图比前面两种对称

TSC999

TSC999

现在的问题是，史勇关于 E、F 点的复坐标公式是怎样算出来的？ 是根据 “复对合理论”  算的？“复对合” 是个啥东东？ 网上没见到史勇先生出版过这个理论的书。
不知哪位大师也能算出  E、F 点的复坐标？ 搬个板凳坐在这里等。

彭翕成

TSC999 发表于 2022-2-3 21:24

根据几何意义可知，BC弧中点就是复数bc。再根据等腰三角形三线合一，可知c方-b方与bc垂直。群里几个人已经建群，如果你愿意加入，可加我微信13720152511，方便交流一些

dlsh

把BC最小和线段乘积等于平方差改一下，类似的线段可能有三条