史勇的一个经典几何案例

TSC999

求 E 点坐标的方法：


求 E 点坐标的程序代码如下：

1. Clear["Global`*"];
   
2. h = a^2 + b^2 + c^2;  
   
3. \!\(\*OverscriptBox[\(h\), \(_\)]\) = 1/a^2 + 1/b^2 + 1/c^2;
   
4. Timing[Simplify[
   
5.   Solve[{Sqrt[(a^2 - b^2) (1/a^2 - 1/b^2)] Sqrt[(b^2 - e) (1/b^2 -
   
6. \!\(\*OverscriptBox[\(e\), \(_\)]\))] == (a^2 - c^2) (1/a^2 -
   
7.          1/c^2) - (b^2 - c^2) (1/b^2 - 1/c^2), (h - b^2)/(
   
8. \!\(\*OverscriptBox[\(h\), \(_\)]\) - 1/b^2) == (e - b^2)/(
   
9. \!\(\*OverscriptBox[\(e\), \(_\)]\) - 1/b^2)}, {e}, {
   
10. \!\(\*OverscriptBox[\(e\), \(_\)]\)}]]]

复制代码

求 F 点坐标的程序代码如下：

1. Clear["Global`*"];
   
2. h = a^2 + b^2 + c^2;  
   
3. \!\(\*OverscriptBox[\(h\), \(_\)]\) = 1/a^2 + 1/b^2 + 1/c^2;
   
4. Timing[Simplify[
   
5.   Solve[{Sqrt[(a^2 - c^2) (1/a^2 - 1/c^2)] Sqrt[(c^2 - f) (1/c^2 -
   
6. \!\(\*OverscriptBox[\(f\), \(_\)]\))] == (a^2 - b^2) (1/a^2 -
   
7.          1/b^2) - (b^2 - c^2) (1/b^2 - 1/c^2), (h - c^2)/(
   
8. \!\(\*OverscriptBox[\(h\), \(_\)]\) - 1/c^2) == (f - c^2)/(
   
9. \!\(\*OverscriptBox[\(f\), \(_\)]\) - 1/c^2)}, {f}, {
   
10. \!\(\*OverscriptBox[\(f\), \(_\)]\)}]]]

复制代码

E 点和 F 点未化简公式表达：



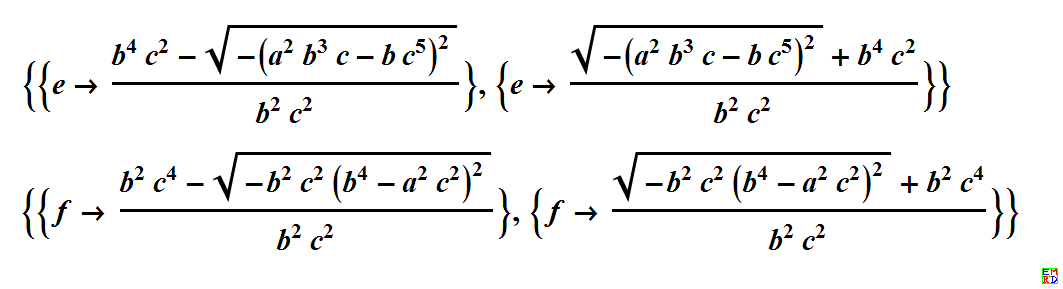
上面公式中如何化简根式？ 即如何确定开方后取正号还是负号，可以用具体数字代入公式验证确定，与实际测量结果一致才行。

dlsh

dlsh

另外一种构图顺序，参考https://bbs.emath.ac.cn/thread-18285-1-1.html

TSC999

把主帖中的原命题改一下，就能适用于任何形状的三角形，也不必限制 BC 边为最短边这个要求了。新命题如下：



对于钝角三角形，命题也是成立的：

dlsh

上楼的命题还要改进

TSC999

命题改为下面这个说法，就没有毛病了。