一个结构非常优美的复数问题

hujunhua

转自单墫的微信公众号“单谈数学”

hujunhua

大家觉得，后两页有必要么？

wayne

还不如直接消元来的简洁. 我的目标是以a为变元, 求b,c. 过程如下:

`a^2(b+c)=(b+c)(b-c)=b^2-c^2 =b+c-2a\\→b+c = \D\frac{2a}{1-a^2}`
又  $b-c=a^2$
所以 `b = \D \frac{a}{1-a^2}+\frac{a^2}{2}, \\c=\D  \frac{a}{1-a^2}-\frac{a^2}{2}`

代入另外两个式子其一, 得到

       $a^2 (a^6-3 a^2+6)=0$

于是 $(a+b+c)^2 = (a+\frac{2a}{1-a^2})^2  = \frac{a^6-6a^4+9a^2}{(1-a^2)^2}= \frac{-6-6a^4+12a^2}{(1-a^2)^2}= -6 $  
一点都不拖泥带水.

mathe

我也喜欢用对称式来做，
全部相加有$a^2+b^2+c^2=0$ (1)
设$s=a+b+c$,两边平方，根据(1)得到$ab+bc+ca=s^2/2$ (2)
三式分别乘以a,b,c相加得到$a^3+b^3+c^3=0$ (3)
由于$a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)=-s^3/2$，得到$abc=s^3/6$ (4)
将原始三式平方以后相加得到$a^4+b^4+c^4=-2(ab+bc+ca)=-s^2$ (5)
再将(1)两边平方得到$a^4+b^4+c^4+2(a^2b^2+b^2c^2+c^2a^2)=0$,即$a^2b^2+b^2c^2+c^2a^2=s^2/2$(6)
见那个(2)式再平方得到$a^2b^2+b^2c^2+c^2a^2+2abc(a+b+c)=s^4/4$,即$s^2/2+2s^3/6*s=s^4/4$,
简化后得到$6s^2=-s^4$，故s=0或$s^2=-6$

uk702

反过来，对于任意的 a，选取 b、c 满足 \( b+c=\pm \sqrt{6} \ i - a \)，\( b-c = a^2  \) 是否都满足题目的要求？

hujunhua

我觉得后两页是多余的原因在于：
1、原方程组秩与变量相等，因此恰好具有有限确定的解
2、原方程组三个等式是轮换对称的，故其解`a, b, c`可以满足同一个一元3次方程。如果用消元法消去任意两个变量，得到的必是同一个方程。
3、所以，通过对称多项式的等价变换得到`a+b+c, ab+bc+ca, abc`的值，就确定了那个一元3次方程的各项系数。它的解自然是原方程组的解。

wayne

mathe的解答过程,我重新整理一下,使得更清晰. 然后, 我们再尝试推导一下$a^n+b^n+c^n$的值
设$e_1=a+b+c, e_2=ab+bc+ca, e_3=abc$,那么$p_n=a^n+b^n+c^n$可以用$e_1,e_2,e_3$ 表达出来. 然后我们先处理一下初始条件:$p_1=e_1, p_2=0,p_3=0, p_4= 2p_2^2-2e_2$
由 $p_2 = e_1^2-2 e_2 = 0, p_3 =e_1^3-3 e_2 e_1+3 e_3 = 0$得到$e_2 = \frac{e_1^2}{2},e_3 =\frac{e_1^3}{6}$ ,  代入$ p_4 = e_1^4-4 e_2 e_1^2+4 e_3 e_1+2 e_2^2  = 2p_2^2-2e_2$ 可以得到$e_1^2+6=0$, 好了,初始条件处理完毕, 按下不表.
继续, $p_n=a^n+b^n+c^n = f(e_1,e_2,e_3)$,而 $f(e_1,e_2,e_3)$的项 是方程 $e_1+2e_2+3e_3=n$的非负整数解. 至于系数好像有点难度,  只能靠递推了? [这个节外生枝,跟本题无关]

1. Table[{n,First[SymmetricReduction[PowerSymmetricPolynomial[n,{a,b,c}],{a,b,c},{Subscript[e, 1],Subscript[e, 2],Subscript[e, 3]}]]},{n,10}]

复制代码

\[\begin{array}{l}
\left\{1,e_1\right\} \\
\left\{2,e_1^2-2 e_2\right\} \\
\left\{3,e_1^3-3 e_2 e_1+3 e_3\right\} \\
\left\{4,e_1^4-4 e_2 e_1^2+4 e_3 e_1+2 e_2^2\right\} \\
\left\{5,e_1^5-5 e_2 e_1^3+5 e_3 e_1^2+5 e_2^2 e_1-5 e_2 e_3\right\} \\
\left\{6,e_1^6-6 e_2 e_1^4+6 e_3 e_1^3+9 e_2^2 e_1^2-12 e_2 e_3 e_1-2 e_2^3+3 e_3^2\right\} \\
\left\{7,e_1^7-7 e_2 e_1^5+7 e_3 e_1^4+14 e_2^2 e_1^3-21 e_2 e_3 e_1^2-7 e_2^3 e_1+7 e_3^2 e_1+7 e_2^2 e_3\right\} \\
\left\{8,e_1^8-8 e_2 e_1^6+8 e_3 e_1^5+20 e_2^2 e_1^4-32 e_2 e_3 e_1^3-16 e_2^3 e_1^2+12 e_3^2 e_1^2+24 e_2^2 e_3 e_1+2 e_2^4-8 e_2 e_3^2\right\} \\
\left\{9,e_1^9-9 e_2 e_1^7+9 e_3 e_1^6+27 e_2^2 e_1^5-45 e_2 e_3 e_1^4-30 e_2^3 e_1^3+18 e_3^2 e_1^3+54 e_2^2 e_3 e_1^2+9 e_2^4 e_1-27 e_2 e_3^2 e_1+3 e_3^3-9 e_2^3 e_3\right\} \\
\left\{10,e_1^{10}-10 e_2 e_1^8+10 e_3 e_1^7+35 e_2^2 e_1^6-60 e_2 e_3 e_1^5-50 e_2^3 e_1^4+25 e_3^2 e_1^4+100 e_2^2 e_3 e_1^3+25 e_2^4 e_1^2-60 e_2 e_3^2 e_1^2+10 e_3^3 e_1-40 e_2^3 e_3 e_1-2 e_2^5+15 e_2^2 e_3^2\right\} \\
\end{array}\]

通过肉眼观察+Mathematica代码验证,发现 $p_n=a^n+b^n+c^n = f(e_1,e_2,e_3) = n*\sum_{{x_1,x_2,x_3}}\frac{(-1)^{x_2}*(x_1+x_2+x_3-1)!}{x_1! x_2! x_3!}* e_1^{x_1}e_2^{x_2}e_3^{x_3}$,其中${x_1,x_2,x_3}$遍历 方程$e_1+2e_2+3e_3=n$的所有非负整数解${x_1,x_2,x_3}$.

1. Clear[p];{p[1],p[2],p[3]} = Table[First[SymmetricReduction[PowerSymmetricPolynomial[i,{a,b,c}],{a,b,c},{Subscript[e, 1],Subscript[e, 2],Subscript[e, 3]}]],{i,3}];
   
2. pool=Table[If[k<4,p[k],p[k]=Expand[Sum[(-1)^(k+i-1) Subscript[e,k-i]p[i],{i,k-3,k-1}]]],{k,100}];sol=Table[{a,b,offset={a,b}.{2,3},FullSimplify[(-1)^a n  Binomial[a+b,a]/(a+b) Binomial[n-(a+2b+1),n-(2a+3b)]-Block[{e23={a,b},offset},offset=e23.{2,3};Factor[FindSequenceFunction[Table[Association[CoefficientRules[pool[[n]]]][{n-offset,e23[[1]],e23[[2]]}],{n,offset+1,offset+20}],n]]/.n->(n-offset)]]},{a,0,10},{b,1,10}]

复制代码

我还以为这个是我的原创了,后来发现Wikipedia上已经有这个公式了, https://en.wikipedia.org/wiki/Newton%27s_identities

1. With[{n=134},Total[n Function[{x,y,z},(-1)^y  Multinomial[x,y,z]/(x+y+z)  Subscript[e, 1]^x Subscript[e, 2]^y Subscript[e, 3]^z]@@@SolveValues[x+2y+3z==n&&x>=0&&y>=0&&z>=0,{x,y,z},Integers]]]

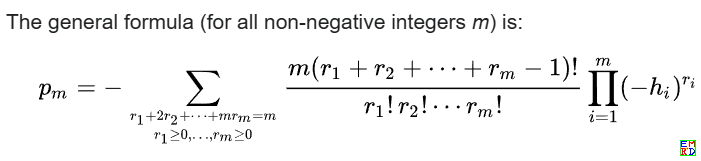
复制代码

nyy

没看懂

hujunhua

wayne 发表于 2024-4-26 10:41
mathe的解答过程,我重新整理一下,使得更清晰. 然后, 我们再尝试推导一下$a^n+b^n+c^n$的值
设$e_1=a+b+c, e ...

`p_n`的SymmetricReduction是牛顿多项式的基本问题, 哪里轮得到现在来原创。
所以我也想过求`p_n`, 但仅限于将本题的具体值代入后的复数序列，而非一般公式。
为此，可使用递推公式\[p_{n}=e_1·p_{n-1}-e_2·p_{n-2}+e_3·p_{n-3}=(p_{n-1}-p_{n-3})e_1+3p_{n-2}\]初值 `p_0=3, p_1=e_1=\sqrt{-6}，p_2=0，p_3=0`
由此可递推计算前几项为`p_4=-e_1^2=6,p_5=6e_1, p_6=3e_1^2=-18`
显然，奇数项是0或者纯虚数，偶数项是实数。因此奇偶项分开处理应更方便。
记`P_n=p_{2n},Q_n=p_{2n-1}/e_1`, 从3#已经知道`a^2, b^2, c^2`是方程\[x^3-3x+6=0\]的根，那么此即`P_n,Q_n`的递推公式所对应的特征方程，于是必有\[
P_{n}=3P_{n-2}-6P_{n-3}，(n>2, P_0=3, P_1=0, P_2=6)
\]\[Q_{n}=3Q_{n-2}-6Q_{n-3},(n>3,Q_1=1, Q_2=0,Q_3=6)
\]由此可递推计算得\[P_n: 3, 0, 6, -18, 18, -90, 192, -378, 1116, ...\]\[Q_n: 1,0,6,-6,18,-54,90,-270,594,......\]
我计算的目的之一是想知道后面是否还有 `p_n=0`, 按递推公式及正反馈的正负振荡可知没有了。

wayne

hujunhua 发表于 2024-4-27 02:15
`p_n`的SymmetricReduction是牛顿多项式的基本问题, 哪里轮得到现在来原创。
所以我也想过求`p_n`, 但仅 ...

对于给定的$n$, 求$p_n$的对称多项式, 用SymmetricReduction是可以的, 但对于较大的$n$,Mathematica就慢很多很多了. 然后对一般的$n$, Mathematica就更没办法了.  然后我要解决的就是较大的n和一般的n. 这两个目标都已经达成了,比SymmetricReduction快很多.