- 注册时间
- 2012-4-20
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 3498
- 在线时间
- 小时
|
 发表于 2025-2-16 15:26:32
|
显示全部楼层
发表于 2025-2-16 15:26:32
|
显示全部楼层
基于有理表示的解答如下:
令\(\mathop {BA}\limits^ \to = \frac{{(s + t)(1 - st)}}{{s{{(1 - it)}^2}}}\mathop {BC}\limits^ \to \), 则其余各点有表示
\[\left\{ \begin{array}{l}
\mathop {B{A_1}}\limits^ \to = \frac{{(s + t)( - 1 + st)}}{{s(1 + {t^2})}}\mathop {BC}\limits^ \to , \qquad \mathop {B{A_2}}\limits^ \to = \frac{{\left( {s + t} \right)\left( {1 + st} \right)}}{{s\left( {1 + {t^2}} \right)}}\mathop {BC}\limits^ \to \\
\mathop {B{B_1}}\limits^ \to = \frac{{2i\left( {s + t} \right)}}{{\left( {i + s} \right)\left( {i + t} \right)}}\mathop {BC}\limits^ \to , \qquad \mathop {B{B_2}}\limits^ \to = \frac{{2i\left( {s + t} \right)\left( { - 1 + st} \right)}}{{s\left( {i + s} \right){{\left( {i + t} \right)}^2}}}\mathop {BC}\limits^ \to \\
\mathop {B{C_1}}\limits^ \to = \frac{{ - s - 2t + s{t^2}}}{{s{{\left( {i + t} \right)}^2}}}\mathop {BC}\limits^ \to , \qquad \mathop {B{C_2}}\limits^ \to = \frac{{ - i + t}}{{i + t}}\mathop {BC}\limits^ \to
\end{array} \right.\]
六点的外接圆锥曲线上的点$P$,若设为 \(\mathop {BP}\limits^ \to = (x+y i)\mathop {BC}\limits^ \to \), 则$x,y$ 满足方程
\[ -4 s^2 \left(t^2+1\right)^2 x^2 \left(s t^2-s-2 t\right)+4 \left(s^2+1\right) s t \left(t^2+1\right) x y (s t-1) \left(2 s t+t^2-1\right)+8 s^2 t \left(t^2+1\right) x (s+t) \left(s t^2-s-2 t\right)-4 \left(t^2+1\right) y (s+t) \left(s^4 t^3+s^3 t^2-s^3+s^2 t^3-3 s^2 t-s t^2+s+t\right)+s \left(t^2+1\right) y^2 \left(3 s^4 t^4-6 s^4 t^2-s^4-12 s^3 t^3+4 s^3 t-2 s^2 t^4+2 s^2-4 s t^3+12 s t-t^4+6 t^2-1\right)-4 (s+t)^2 (s t-1) (s t+1) \left(s t^2-s-2 t\right) = 0 \]
根据圆锥曲线的离心率,中心, 及一个焦点的对应关系,即可反解出三角形$ABC$的位置。不妨以 \( \frac{{{x^2}}}{3} + \frac{{{y^2}}}{2} = 1\) 为例。
其离心率\(e = \frac{1}{{\sqrt 3 }}\), 而根据上述方程,离心率\(e\)满足:
\[\frac{{{{\left( { - 1 + 6{s^2} - {s^4} + 20st + 4{s^3}t + 6{t^2} - 6{s^4}{t^2} + 4s{t^3} - 12{s^3}{t^3} - {t^4} - 6{s^2}{t^4} + 3{s^4}{t^4}} \right)}^2}}}{{4({s^2} - 2{s^4} + {s^6} + 2st - 16{s^3}t - 2{s^5}t + {t^2} - 28{s^2}{t^2} - 7{s^4}{t^2} + 6{s^6}{t^2} - 16s{t^3} - 12{s^3}{t^3} + 20{s^5}{t^3} - 2{t^4} - 7{s^2}{t^4} + 44{s^4}{t^4} + 9{s^6}{t^4} - 2s{t^5} + 20{s^3}{t^5} - 6{s^5}{t^5} - 12{s^7}{t^5} + {t^6} + 6{s^2}{t^6} + 9{s^4}{t^6} - 8{s^6}{t^6} + 4{s^8}{t^6} - 12{s^5}{t^7} + 4{s^7}{t^7} + 4{s^6}{t^8})}} = \frac{{{{\left( {{e^2} - 2} \right)}^2}}}{{{e^2} - 1}} = -\frac{25}{6} \]
我们可以任意指定其中一个参数的值, 例如令\(s=\frac{1}{2}\), 在\(s>0, t>0 , 1-s t >0 \)的限定下由此求解得到两个\(t\)值:
\[ \left\{\left\{t\to \text{Root}\left[4907 \text{$\#$1}^8-6176 \text{$\#$1}^7+18012 \text{$\#$1}^6-17376 \text{$\#$1}^5+19810 \text{$\#$1}^4-22544 \text{$\#$1}^3+7252 \text{$\#$1}^2-6544 \text{$\#$1}+1947\&,1,0\right]\right\},\left\{t\to \text{Root}\left[4907 \text{$\#$1}^8-6176 \text{$\#$1}^7+18012 \text{$\#$1}^6-17376 \text{$\#$1}^5+19810 \text{$\#$1}^4-22544 \text{$\#$1}^3+7252 \text{$\#$1}^2-6544 \text{$\#$1}+1947\&,2,0\right]\right\}\right\} \]
任取其中一个, 例如第二个\(t \approx 1.017893063\), 代入前面的曲线方程,得到
\[ - 13.778713532642314 - 12.695139134788366x + 8.364973769896583{x^2} - 7.052854870822432y - 2.6817095284084016xy + 6.9040839776331495{y^2} = 0\]
由此得到其中心\(O\)和焦点\(F_1, F_2\)的表示:
\[\begin{array}{l}
\mathop {BO}\limits^ \to = (0.8677139887758467 + 0.6792944417277683i)\mathop {BC}\limits^ \to \\
\mathop {B{F_1}}\limits^ \to = (0.3121747404006916 - 0.2559648633817677i)\mathop {BC}\limits^ \to \\
\mathop {B{F_2}}\limits^ \to = (1.4232532371510018 + 1.6145537468373043i)\mathop {BC}\limits^ \to
\end{array}\]
将 \(O = 0, F_1=1, F_2=-1\) 代入上式,即可解出\(B, C\) 两点:
\[\begin{array}{l}
B = 0.9442522488063225 - 0.36689803814060307i\\
C = 0.4747826562223814 + 0.42346161010085903i
\end{array}\]
再由\(\mathop {BA}\limits^ \to = \frac{{(s + t)(1 - st)}}{{s{{(1 - it)}^2}}}\mathop {BC}\limits^ \to \) 给出\(A\)点
\[A = 0.37177738441867947 - 0.7208271131052225i\]
画图验证一下:
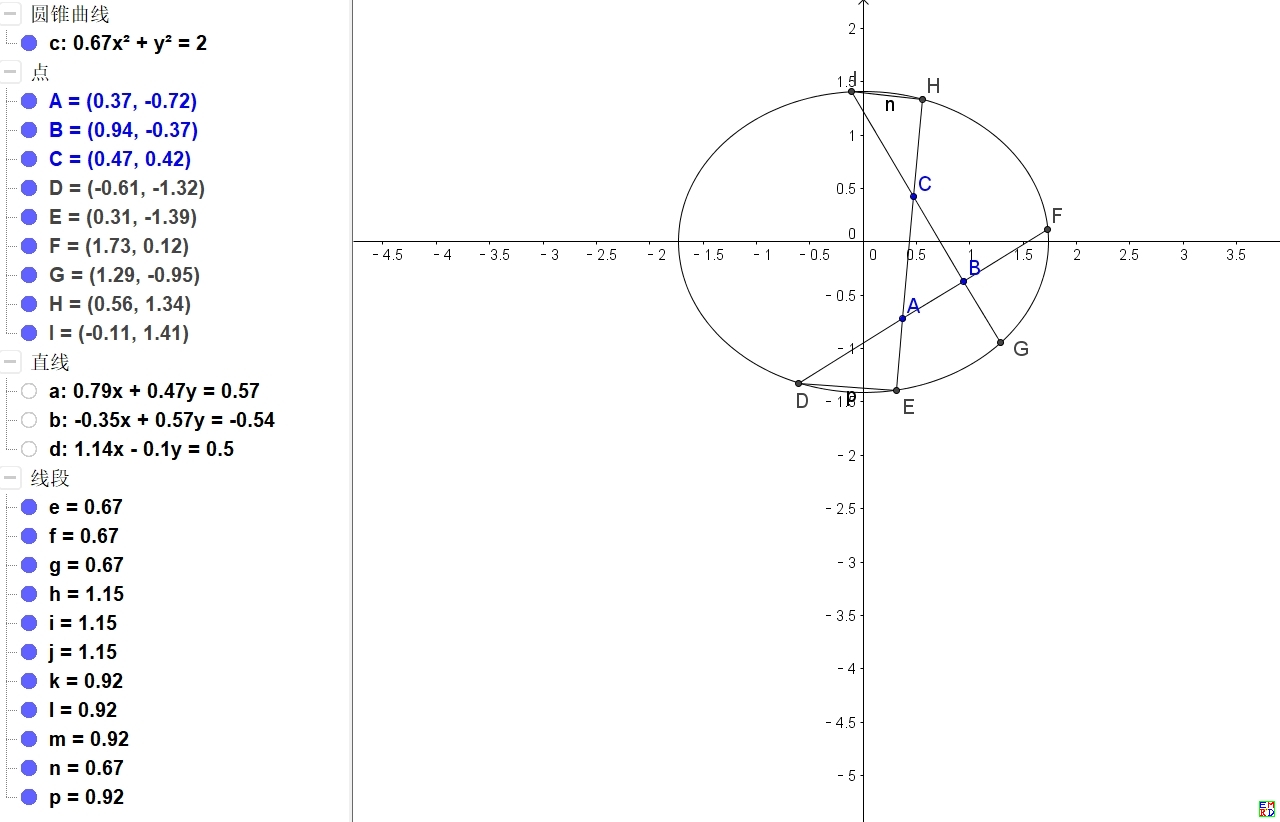
|
评分
-
| 参与人数 1 | 威望 +6 |
金币 +6 |
贡献 +6 |
经验 +6 |
鲜花 +6 |
收起
理由
|
 wayne wayne
| + 6 |
+ 6 |
+ 6 |
+ 6 |
+ 6 |
不明觉厉! |
查看全部评分
|