怪兽分裂

mathe

由于红色路径只有两种方向，总可以假设总是向坐下和右下发展。经检验发现最下面红色端点总带着两个蓝色点，可以不需要记录。
而上面蓝色点有些复杂，特别是红色路径形成一条直线时，可以时两个蓝点，其余情况应该都一个蓝点，但是有两种可能方向。最多不超过3比特信息。

mathe

由于规范化后路径每个点总是向左下或向右下移动，而整个图进行左右翻转也时等价的，总可以假设顶上第一个蓝点到红点是向左下移动的，
比如下面的图(a9)不符合上面蓝点到红点是向右下移动的，所以需要进行左右翻转。
.
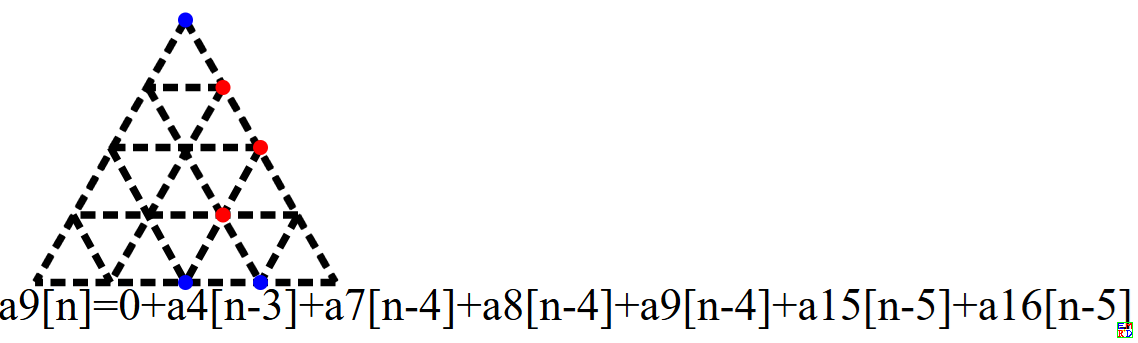然后我们一次查看每个红点到下一个红点的移动方向，如果向左下，编码为0，如果向右下，编码为1.
而由于最下面红点下方总是两个蓝点，可以不编码。由此，对于包含n个红点的图，编码后是n-1比特的整数。
而如下面(a10)这样的图，由于所有红色点在一条直线上，可以顶上偏右多一个蓝色点，我们在编码中可以忽略这个蓝色点，于是下面图会编码为n-1个比特0.

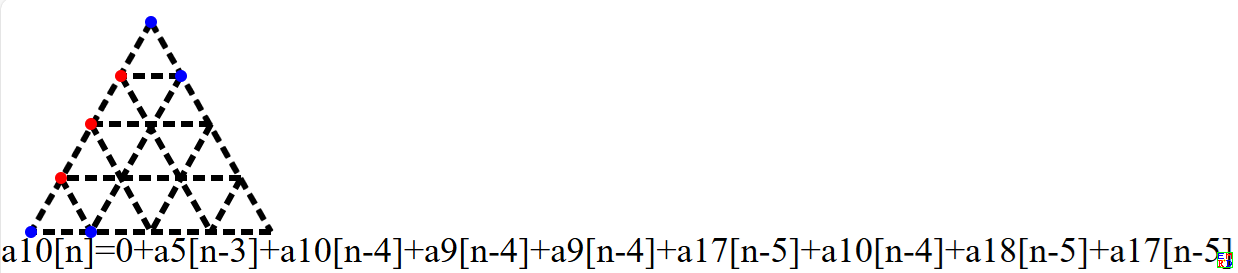
也就是对于全0的编码，我们会认为它顶上偏右位置多一个蓝色点。
而相应的如下图(a7)这样的图，所有红色点也在一条直线上，但是顶上只有一个蓝点，会被编码成全1.
。

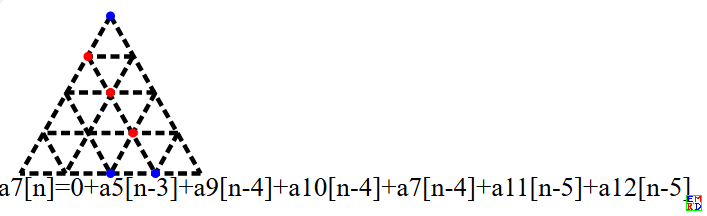特别的图a3只有一个红点，编码为0个比特（这时无所谓0，1了）。而图a2和a1只能特殊处理，不参与编码。


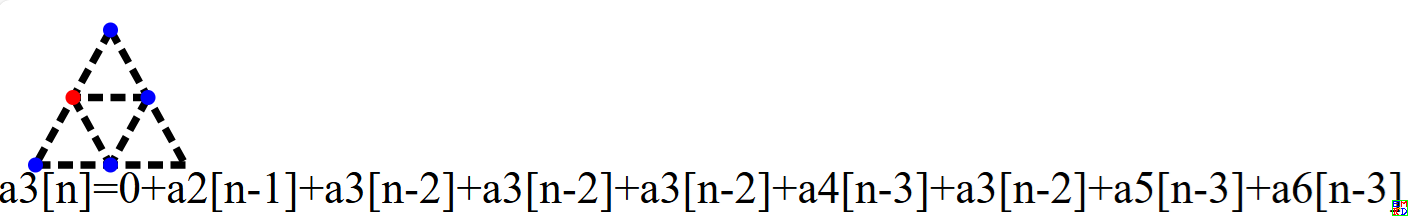
于是在这种编码方案下面，如果一个图的编码是n比特x，那么分裂m次后可以达到一个目标状态的方案数为f(n,x,m)，那么可以得到递推式
当\(n\ge 1\)时
f(n,x,m)=f(n, x, m-n-2)+f(n+1,x, m-n-3)+((x==0)+1)f(n+1,x|(1<<n),m-n-3)
            + f(n-1, r, m-n-1)+f(n,r,m-n-2)+((x==0)+1)f(n,r|(1<<(N-1)), m-n-2);
  其中在x是偶数时，r=x/2, x是奇数时，r=~(x/2) (这里~表示对这个n-1比特数取反）
而当\(n==0\)时，x无编码，对应
f(0,.,m)=a2(m-1)+4f(0,.,m-2)+2f(1,1,m-3)+f(1,0,m-3)
而
a2(0)=1
a2(m)=3a2(m-1)+3f(0,.,m-2) (当\(m\ge 1\))
当然，对于任意\(m\lt \frac{(n+2)(n+1)}2\) , f(n,.,m)=0.

而分析计算结果可以发现，对于给定的n,m, f(n,x,m)的取值只和x的第一个同最高位不同的比特位的位置相关。这个从递推式里面也容易看出，可以考虑对m+n进行从小到大的归纳假设进行分析。
另外发现x除了全0和全1，x取互补值时函数值相同， 但是这个性质比较难分析，不过我们计算时，还是可以将这两者各自单独计算，这部分复杂度不大。
由此，我们只需要计算f(n,11..110...,m)和f(n,00...01...,m)即可。
我们可以记u(n,k,m)为前面正好有k个1的情况，v(n,k,m)为前面有正好k个0的情况，(\(1\le k \le n\))
于是
u(n,k,m)=u(n,k,m-n-2)+v(n+1,1,m-n-3)+u(n+1,k+1,m-n-3)
         +u(n-1,h,m-n-1)+v(n,1,m-n-2)+u(n,h+1,m-n-2)
其中h在k<n时等于k,在k==n时h=k-1.
同样
v(n,k,m)=v(n,k,m-n-2)+v(n+1,k+1,m-n-3)+((k==n)+1)u(n+1,1,m-n-3)
    +v(n-1,h,m-n-1)+v(n,h+1,m-n-2)+((k==n)+1)u(n,1,m-n-2)
  其中h在k<n时等于k,在k==n时h=k-1.
于是可以看出，除了k==n的情况，其他情况可以通过归纳形式证明u(n,k,m)=v(n,k,m), 我们可以统一记为w(n,k,m) (\(1\le k\le n-1, m\ge \frac{(n+1)(n+2)}2\)),
而由于u(n,n,m)和v(n,n,m)可能不同，可以把它们简记为u(n,m)和v(n,m).

而其中初始条件为u(0,.,m)=v(0,.,m)=f(0,.,m)=a2(m-1)+4u(0,.,m-2)+2u(1,1,m-3)+v(1,1,m-3)=a2(m-1)+4u(0,.,m-2)+2u(1,m-3)+v(1,m-3).

mathe

使用这个更改过的代码，可以轻松计算到前一万项
比如第1000项是
847371597789571966659994286535266912661575042192955911470042915186009346713402175688300668749106201719524728919753348103884058340643567001844715647009401975955914925465690034575670917214852365428925108358739372296709796011959211240792191889047543164424746244438701355495677143126915042215726913350780554308574278556160334364540185257762297512745227151912029515331777628922526140762760904175634426935087991859776977764590252347674848727315174042790543722164590886010770636179992050632917962274098461774865528389425897074954044479480
而前2000项在下面附件中
monster2000.zip (483.15 KB, 下载次数: 2)

6 天前 上传

点击文件名下载附件

王守恩

正确答案——1, 3, 9, 30, 99, 336, 1134, 3855, 13086, 44499, 151263, 514419, 1749267, 5949063, 20231571, 68805717, 234000357, 795815145, 2706494328, 9204559704, 31303919946, 106462016427, 362068382670, 1231364375880,  

偏小答案——1, 3, 9, 30, 99, 336, 1134, 3855, 13086, 44499, 151263, 514419, 1749267, 5949063, 20231569, 68805684, 234000161, 795814072, 2706489250, 9204537063, 31303824386, 106461625974, 362066830913, 1231358327747,
RecurrenceTable[{a[1] == 1, a[2] == 3, a[3] == 9, a[4] == 30, a[5] == 99, a[6] == 336, a[n] == Ceiling[(3 a[n - 1] + 4 a[n - 2] - 17 a[n - 3]/3 - 10 a[n - 4] - 31 a[n - 5]/3 + 21 a[n - 6])]}, a[n], {n, 45}]

偏大答案——1, 3, 9, 30, 99, 336, 1135, 3859, 13103, 44561, 151485, 515187, 1751918, 5958119, 20262486, 68910965, 234358571, 797033404, 2710637217, 9218645192, 31351808346, 106624819235, 362621847648, 1233245904246,
RecurrenceTable[{a[1] == 1, a[2] == 3, a[3] == 9, a[4] == 30, a[5] == 99, a[6] == 336, a[n] == Ceiling[(3 a[n - 1] + 4 a[n - 2] - 17 a[n - 3]/3 - 10 a[n - 4] - 31 a[n - 5]/3 + 21 a[n - 6]) (1 + 1/n^n)]}, a[n], {n, 45}]

偏小答案 < 正确答案 < 偏大答案。 通项公式不好找。

iseemu2009

mathe 发表于 2025-4-13 06:59
使用这个更改过的代码，可以轻松计算到前一万项
比如第1000项是
8473715977895719666599942865352669126615 ...

mathe，把代码发一下吧，研究学习。