- 注册时间
- 2009-5-22
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 38777
- 在线时间
- 小时
|
楼主 |
发表于 2009-12-24 10:48:02
|
显示全部楼层
我昨天干坏事了,把这张帖子每分钟刷新1次,连续刷了半天,结果这张帖子成了一周内最热门的帖子……
还有那张northwolves的帖子也是。 这道题Fans在12月20日23点30分才完美解决,比比赛结束时间晚了1小时30分。
这道题Fans在12月20日23点30分才完美解决,比比赛结束时间晚了1小时30分。 所用的方法极其暴力。
首先令$n_2=0$,$m_2=0$,考虑$n_1$和$m_1$的变化,把测试结果列成一张表。
所用的方法极其暴力。
首先令$n_2=0$,$m_2=0$,考虑$n_1$和$m_1$的变化,把测试结果列成一张表。
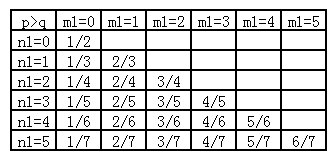 规律是显而易见的。
然后令$n_2=1$,$m_2=0$,同样考虑$n_1$和$m_1$的变化,把测试结果列成第2张表。
规律是显而易见的。
然后令$n_2=1$,$m_2=0$,同样考虑$n_1$和$m_1$的变化,把测试结果列成第2张表。
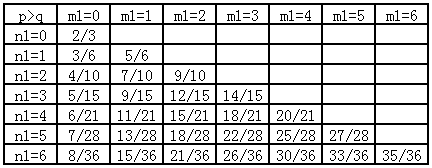 规律也是显而易见的。
然后令$n_2=1$,$m_2=1$,同样考虑$n_1$和$m_1$的变化,把测试结果列成第3张表。
规律也是显而易见的。
然后令$n_2=1$,$m_2=1$,同样考虑$n_1$和$m_1$的变化,把测试结果列成第3张表。
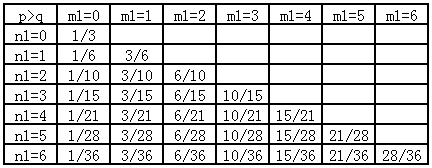 规律就更显而易见了。
然后令$n_2=2$,$m_2=0$,同样考虑$n_1$和$m_1$的变化,把测试结果列成第4张表。
规律就更显而易见了。
然后令$n_2=2$,$m_2=0$,同样考虑$n_1$和$m_1$的变化,把测试结果列成第4张表。
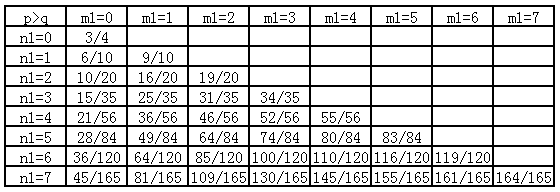 规律不怎么显而易见,不过肯定还是能找到的。
然后令$n_2=2$,$m_2=1$,同样考虑$n_1$和$m_1$的变化,把测试结果列成第5张表。
规律不怎么显而易见,不过肯定还是能找到的。
然后令$n_2=2$,$m_2=1$,同样考虑$n_1$和$m_1$的变化,把测试结果列成第5张表。
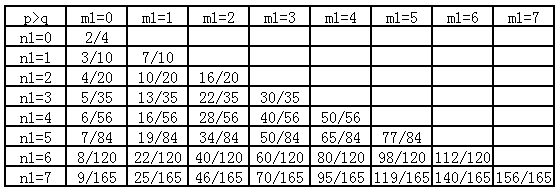 规律也是不怎么显而易见,不过肯定还是能找到的,继续努力。
接着令$n_2=2$,$m_2=2$,同样考虑$n_1$和$m_1$的变化,把测试结果列成第6张表。
规律也是不怎么显而易见,不过肯定还是能找到的,继续努力。
接着令$n_2=2$,$m_2=2$,同样考虑$n_1$和$m_1$的变化,把测试结果列成第6张表。
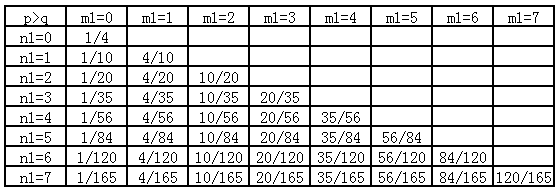 这个规律显而易见多了。
接下来令$n_2=3$,$m_2=0$,同样考虑$n_1$和$m_1$的变化,把测试结果列成第7张表。
这个规律显而易见多了。
接下来令$n_2=3$,$m_2=0$,同样考虑$n_1$和$m_1$的变化,把测试结果列成第7张表。
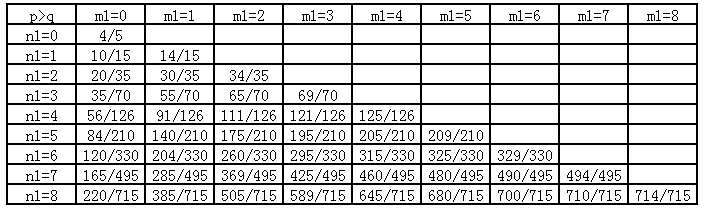 如果前面的规律都找到了,现在这些表格的规律应该一眼就看出来了。
接下来令$n_2=3$,$m_2=1$,同样考虑$n_1$和$m_1$的变化,把测试结果列成第8张表。
如果前面的规律都找到了,现在这些表格的规律应该一眼就看出来了。
接下来令$n_2=3$,$m_2=1$,同样考虑$n_1$和$m_1$的变化,把测试结果列成第8张表。
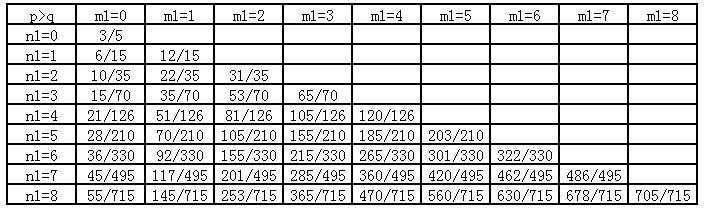 如果前面的规律都找到了,现在这些表格的规律应该一眼就看出来了。
继续令$n_2=3$,$m_2=2$,同样考虑$n_1$和$m_1$的变化,把测试结果列成第9张表。
如果前面的规律都找到了,现在这些表格的规律应该一眼就看出来了。
继续令$n_2=3$,$m_2=2$,同样考虑$n_1$和$m_1$的变化,把测试结果列成第9张表。
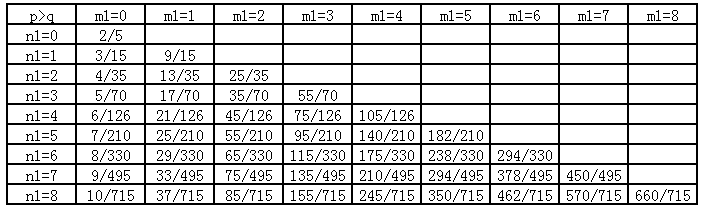 如果前面的规律都找到了,现在这些表格的规律应该一眼就看出来了。
最后令$n_2=3$,$m_2=3$,同样考虑$n_1$和$m_1$的变化,把测试结果列成第10张表。
如果前面的规律都找到了,现在这些表格的规律应该一眼就看出来了。
最后令$n_2=3$,$m_2=3$,同样考虑$n_1$和$m_1$的变化,把测试结果列成第10张表。
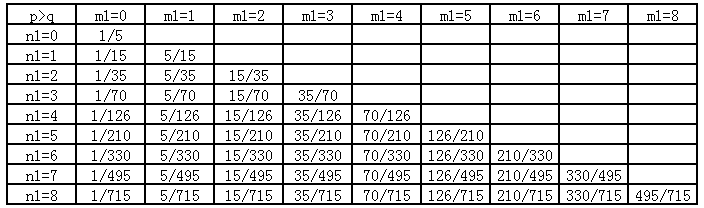 如果前面的规律都找到了,现在这些表格的规律应该一眼就看出来了。
好了,看完这10张表,表里的规律和表与表之间的变化规律是不是都找出来了呢?
如果都找出来了,那么就可以用含有$n_1$、$m_1$、$n_2$、$m_2$的式子来表示p>q的概率了:
p>q的概率为$\frac{\sum_{i=0}^{m_1}C_{m_2+i}^{m_2}C_{n_2-m_2+n_1+1-i}^{n_2-m_2}}{\sum_{i=0}^{n_1+1}C_{m_2+i}^{m_2}C_{n_2-m_2+n_1+1-i}^{n_2-m_2}}$
如果预先打好了$C_n^m$的表,上述表达式的结果是很好求的。
代码如下:
如果前面的规律都找到了,现在这些表格的规律应该一眼就看出来了。
好了,看完这10张表,表里的规律和表与表之间的变化规律是不是都找出来了呢?
如果都找出来了,那么就可以用含有$n_1$、$m_1$、$n_2$、$m_2$的式子来表示p>q的概率了:
p>q的概率为$\frac{\sum_{i=0}^{m_1}C_{m_2+i}^{m_2}C_{n_2-m_2+n_1+1-i}^{n_2-m_2}}{\sum_{i=0}^{n_1+1}C_{m_2+i}^{m_2}C_{n_2-m_2+n_1+1-i}^{n_2-m_2}}$
如果预先打好了$C_n^m$的表,上述表达式的结果是很好求的。
代码如下:-
-
- #include<cstdio>
- #include<memory>
- #include<math.h>
-
- double c[1024][1024],x,y,s,p,q;
- int i,j,k,t,n1,n2,p2,m1,m2;
-
- int main()
- {
- for(i=0;i<1024;i++)
- {
- c[i][0]=1e-153;
- c[i][i]=1e-153;
- for(j=1;j<i;j++)
- c[i][j]=c[i-1][j]+c[i-1][j-1];
- }
- while(scanf("%d%d%d%d",&n1,&m1,&n2,&m2)>3)
- {
- p2=n2-m2;
- p=0;
- q=0;
- for(i=0;i<n1+2;i++)
- {
- s=c[m2+i][m2]*c[p2+n1+1-i][p2];
- q+=s;
- if(i<=m1)p+=s;
- }
- printf("%.9lf\n",p/q);
- }
- return 0;
- }
-
 Coins2_2.rar
(38.9 KB, 下载次数: 2)
由于Fans大牛水平不足,不知道如何从积分式出发,推导出上述表达式。
所以这个工作只好交给更高级的大牛们来完成了。
Coins2_2.rar
(38.9 KB, 下载次数: 2)
由于Fans大牛水平不足,不知道如何从积分式出发,推导出上述表达式。
所以这个工作只好交给更高级的大牛们来完成了。 |
|