射影几何简介

mathe

mathe对几何比较不熟悉，对射影几何的了解也仅仅是在中学时曾经看过一本射影几何的数。不过前一段事件为了解决果树种植问题，使用了不少射影几何的内容，所以现在准备在这里整理一下关于射影几何的一些知识。不过其中可能有很多不精确的地方，那就需要大家一起纠正补充了。

mathe

1.仿射变换
通常我们经常遇到的几何变换有平移，旋转，拉伸等。此外，还有一种变换(skewing,中文名字我忘了)如
   ${(x'=x+y),(y'=y):}$,这些变换组合在一起就形成了仿射变换。从代数上来看，仿射变换其实就是线性空间中的线性变换，
假设变换前列向量为$v$,变换后为$v'$,变换过程可以写成$v'=Av+b$,其中b是一个任意列向量，A是一个可逆矩阵。
仿射变换的特点之一是对于任何一条直线上两段线段，变换前后两段线段长度的比例保持不变。而平行线经过仿射变换后还是平行。
此外，对于圆锥曲线（椭圆，双曲线，抛物线），仿射变换具有不变性，也就是椭圆（包含特例圆）经过仿射变换后还是椭圆，
双曲线经过仿射变换还是双曲线，同样，抛物线的仿射变换还是抛物线。
而且很显然，对于任意椭圆，我们可以通过仿射变换变成特殊形式:一个圆（只要在短轴方向进行拉伸就可以了）
2.齐次坐标
对于笛卡尔坐标下的一个点$(x,y)$,其齐次坐标可以写成$(kx,ky,k)$,其中k可以是任意一个非0的实数。也就是任何一个点的齐次坐标表示是不唯一的。
（同样对于三维空间的点，我们可以用包含4个数的齐次坐标表示）。在笛卡尔坐标系下，我们会使用方程$ax+by+c=0$表示一条直线。而对应在齐次坐标系
下面，点的坐标写成$(x,y,z)$,那么直线方程对应可以写成$ax+by+cz=0$，或者有时我们会直接用直线的齐次坐标$[a,b,c]$来表示.而使用这种方法，
我们可以发现这条直线上除了正常的点以外，还有点$(-bk,ak,0)$也满足条件，而这个点我无法在平面坐标上表示出来，我们称这种点为无穷远点。
我们可以发现，对于一族平行的直线${ax+by+uz=0|"for any " u}$,它们都经过无穷远点$(-bk,ak,0)$.于是我们得到，无穷远点其实是一族平行线的交点。
而在这种定义之下，射影平面上有一个良好的性质：任意两条直线之间有且只有一个交点（而平行线的交点为无穷远点）。
此外，不同方向的平行线交出的无穷远点不同，所有这些无穷远点构成直线$z=0$，或$[0,0,k]$,我们称这条直线为无穷远直线。
3.投影变换
从几何上来说，我们任意选择一个源平面和一个目的平面以及一个投影中心，将源平面上任意一点映射为它和投影中线的连线同目的平面的交点就是一个投影变换。

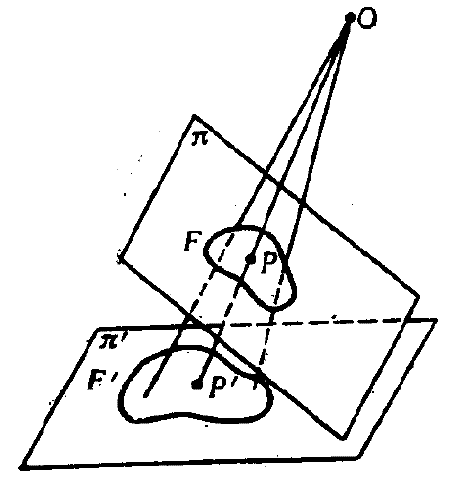
从齐次坐标的表示来看，投影变换很简单，它就是齐次坐标对应的一个线性变换。也就是存在一个3*3可逆矩阵A,使得$(x',y',z')=(x,y,z)A$.
投影变换的复合变换是射影变换，所以任意射影变换都是齐次坐标上的一个线性变换。
而给定4个点${A,B,C,D}$和${A',B',C',D'}$，如果每组内部任意三点不共线，那么必然存在一个唯一的射影变换，将A变换为A',B变换为B',C变换为C',D变换为D'.
同样，给定4条直线${a,b,c,d}$和${a',b',c',d'}$,如果每组内任意三线不共点，同样存在唯一的射影变换，将它们对应变换。
也就是给定4个没有三点共线的点的映射可以确定一个射影变换。同样给定4个没有三线共点的直线的映射可以确定一个射影变换。
而仿射变换可以看成射影变换的一个特例

如下图，设投影中心为圆锥顶点，那么在投影变换下，抛物线，椭圆和双曲线可以相互转化（不同曲线和同一条母线的交点相互对应）


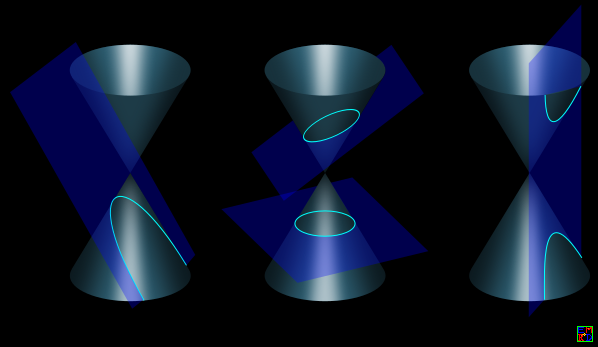
4.交比不变性
对于一条直线上的4个点$A,B,C,D$,交比$[A,B;C,D]$定义为${\bar{AC}:\bar{BC}}/{\bar{AD}:\bar{BD}}$.其中线段上面加横线表示是有向线段。
射影变换的一个重要性质就是保持交比的不变性。利用投影变换的几何意义很容易证明这个性质，假设O是投影中心，将直线l上4个点$A,B,C,D$投影成直线$l'$上四个点
$A',B',C',D'$,那么两条直线上的4个点的交比都可以转化为4个三角形有向面积的比（比如$\bar{AC}:\bar{BC}$等于三角形PAC和PBC的有向面积之比。
然后我们对面积利用正弦定理可以转化为两边和夹角正弦的乘积，如三角形PAC的面积为$1/2*PA*PC*sin/_APC$.代入交比的公式可以消去所有的边，于是结果只同直线
PA,PB,PC,PD的夹角有关。由于上面交比可以只同4个共点直线之间夹角相关，我们可以同样定义4个共点直线的交比，就是任意做一条直线同它们相交得到4个交点的交比。
而交比为－1的4个点具有非常良好的性质。比如给定直线AB，取C为AB的中点，D为这条直线上的无穷远点，那么$[A,B;C,D]=-1$.
同样，对于两条相交的直线a,b,它们的两条角平分线为c,d,那么交比$[a,b;c,d]=-1$ (这个可以利用前一个结论得到，任意作d的平行线e,直线a,b,e构成等腰三角形，c为高
于是直线e和直线a,b,c,d的交点正好是一个中点一个无穷远点，所以交比为－1）
利用交比不变性，我们就可以通过投影变换证明一些比较有趣的命题:
i)如果直线AB//CD,AD和BC交于E,AC和BD交于F,EF交AB于G,那么AG=BG.

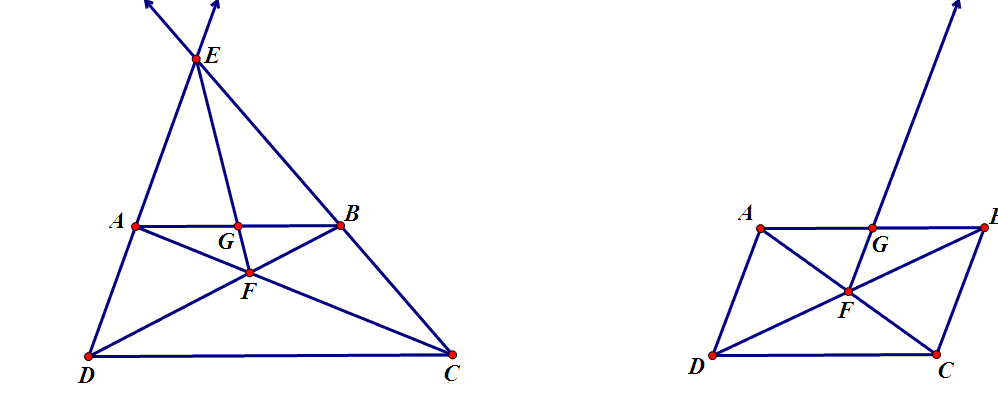
证明，设AB和CD交于无穷远点H,通过射影变换将EH变换成无穷远直线，变换后，AB//CD,AD//BC,于是ABCD是平行四边形，F是平行四边形中心，EF平行边AD,所以平分边AB
而由于投影变换保持四点ABGH的交比不变，所以变换前G也是AB的中点。
ii)三角形的三个外角平分线同对边的交点共线。

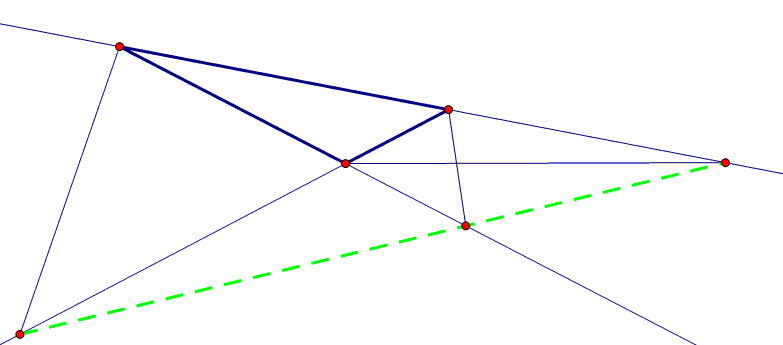
我们将它两个外角平分线同对边交点投影到无穷远，由于两边和对应角的平分线和内角平分线交比为－1，投影后，对应两个角角平分线变成中线。于是第三个角的角平分线也变成
对应边的中线，对应回去，对应的外角平分线和对边的交点也投影到无穷远，于是变换后这三个交点共线（在无穷远线上），所以变换前必然共线。
iii)我们无法通过给定两条线和不在两线上的两个点来确定投影变换。
连接两个点交两条线得出两个交点，这4个点共线，由于投影变换保持交比不变，如果原始给出的这些点的映射的交比和原始四点的交比不同，那么必然无解。
而如果交比相等，那么相当于4个点中有一个点的条件是多于的，等于只给出两条直线和一个点的映射，是无法唯一确定投影变换的（可以在添加一条直线的映射）

mathe

前面讨论的都仅仅是直线（一次曲线），
后面我们还需要讨论圆锥曲线（二次曲线）和椭圆曲线（三次曲线）
待续

wayne

呵呵
我是因为mathe才对射影几何有了了解

gxqcn

小时候只知道两平行线交于“无穷远点”，读了mathe的介绍才有所悟。
期待继续。

mathe

现在我们考虑圆锥曲线。通常二次曲线在笛卡尔坐标系中可以写成$Ax^2+2Bxy+Cy^2+2Dx+2Ey+F=0$，
我们知道$\Delta=B^2-AC$的符号决定了这个二次曲线的类型，如果$\Delta<0$,那么曲线是椭圆（包含特例圆）；
如果$\Delta>0$,那么曲线是双曲线；而如果$\Delta=0$,那么这个曲线是抛物线或退化情况（两条直线）。
类似直线在射影平面的齐次坐标形式是一次齐次表达式，二次曲线在射影平面中的方程是二次齐次表达式
$Ax^2+2Bxy+Cy^2+2Dxz+2Eyz+Fz^2=0$,或者我们可以写成矩阵形式
$[x,y,z][(A,B,D),(B,C,E),(D,E,F)][(x),(y),(z)]=0$，我们可以缩写成$v'Mv=0$,其中v代表列向量$[(x),(y),(z)]$
而其中系数矩阵不可逆的时候是退化情况(两条直线)。椭圆没有点在无穷远点，抛物线同无穷远直线相切，双曲线同无穷远直线相交于两个点。
对于实二次曲线，系数矩阵不能是正定或负定（也就是矩阵特征值必然有正也有负）,不然显然不存在非零向量v满足方程。
由于投影变换可以由一个可逆矩阵P表示,设P的逆矩阵为Q，即$w=Pv,v=Qw$,于是我们得到$w'Q'MQw=0$,
也就是二次曲线变换后曲线的系数矩阵同原系数矩阵可以通过合同变换相互转变。
由于系数矩阵的特征值不全部同号，必然两正一负或两负一正，通过合同变换可以变成
$[(1,0,0),(0,1,0),(0,0,-1)]$或$[(-1,0,0),(0,-1,0),(0,0,1)]$
而我们知道将方程的所有系数变号得到曲线还是原曲线，也就是我们可以将所有非退化二次曲线（即圆锥曲线）通过投影变换
变成曲线$x^2+y^2=z^2$,即单位圆。而由于投影变换是可逆的，我们得到
命题1：任何两条圆锥曲线可以通过射影变换相互转换。
而且如果将一条同圆锥曲线相切的直线投影到无穷远，我们得到抛物线；如果将同圆锥曲线相交的直线投影到无穷远，我们得到双曲线；如果将
同圆锥曲线不相交的直线投影到无穷远，我们得到椭圆（或特例圆）
对于实射影平面上不在给定圆锥曲线上的点，有两类，其中一部分点，我们可以找到过这个点的直线不同圆锥曲线相交，我们称这些点在圆锥曲线的外部。
其中另外一部分点，过这个点的任何直线必然同圆锥曲线相交，我们称这些点在圆锥曲线的内部（显然这种定义在曲线为椭圆时同我们通常的理解是相同的）
对于圆锥曲线外部的任意一个点，圆锥曲线存在两条过这个点的切线，而对于圆锥曲线内部的点，没有切线可以经过它。
而关于圆锥曲线之间通过投影变换的相互转化，我们还可以得到一个更加强的结论
命题2：对于圆锥曲线$Gamma_1,Gamma_2$,任意给定$Gamma_1$上三个点$A_1,B_1,C_1$，以及$Gamma_2$上三个点$A_2,B_2,C_2$,
存在一个射影变换将$Gamma_1$变换为$Gamma_2$,$A_1$变换为$A_2$,$B_1$变换为$B_2$,$C_1$变换为$C_2$.
由于投影变换的可逆性，我们知道证明存在投影变换将$Gamma$变换为单位圆，A变换为点(0,1),B变换为(1,0),C变换为(-1,0)就可以了。
设A的切线和BC的交点为D,B点的切线和C点的切线交于E,那么DE必然同圆锥曲线不相交，只是直接证明有点困难，我们等会再证明这一点。

而如果我们将DE投影到无穷远直线，那么必然将曲线变换成椭圆，A点的切线同BC平行，B点的切线和C点的切线平行；而我们可以再次使用仿射变换将椭圆变换成圆
而仿射变换保持平行线不变，于是我们得到一个圆，其中B点切线和C点切线平行(故BC为直径),A点的切线平行BC,于是我们通过旋转（可能还需要使用翻转）
将A,B,C分别变换到我们所需要的三个点。
现在说明前面得到的直线DE和圆锥曲线不相交，我们只需要通过分步通过投影变换变换曲线就可以了。首先D在曲线外部（切线上的点），可以找到一条过D同曲线不相交的直线
将这条直线投影到无穷远，于是图像变成椭圆，而且A点切线平行BC,通过仿射变换将椭圆变成圆，我们得到圆，其中过A点切线平行BC,所以图像过于过A点直径左右对称。

而E在圆外部（两切线交点）而且在对称轴上，过E点做BC的平行线必然同圆不相交，而这条线就是DE,所以我们证明了DE同这条圆锥曲线不相交。

mathe

上面的命题2非常有用，以至于很多同圆锥曲线相关的命题变得非常显然，比如如果三角形三条边同一个圆锥曲线相切，那么三条切点和顶点的连线三线共点。

现在证明很简单，我们只要通过投影变换将曲线变换为圆，而且三个点在圆上均匀分布，那么三角形就变成了正三角形，而三线显然交于正三角形的中心

mathe

而这点在我们要通过解析几何证明二次曲线相关的题目的时候也会让计算变得非常简单（因为我们可以省掉曲线的方程和另外三个曲线上点的坐标），比如在百度数学吧中，天下无毒_史一直想推销他的“奥妙几何”，其实其实质就是使用了这样的投影变换,将二次曲线固定投影成抛物线$y={x^2}/4$,当然根据命题2还可以指定3个曲线上点的坐标.另外他还采用了参数方程$y=uv,x=u+v$,然后将一些几何定理用他的参数方程来表示,只是他的这个古怪记号弄得别人很难读懂他的内容。
比如链接 http://tieba.baidu.com/f?kz=541378057 中，我将他的例子用投影变换后再用解析几何计算，就非常简单.
实际上对于通常的关于一条二次曲线的几何问题,射影几何说明我们可以任意指定4个点的坐标,通常此后整个问题的变量就会很少,此后使用解析几何自然会简化很多.
而如果使用解析方法,选择将二次曲线变换成抛物线$y=ax^2$或双曲线$xy=a$都是不错的方法,因为曲线上点的横纵坐标之间的关系可以非常容易的表达.(可能用双曲线会更方便一些).
同样,如果我们变换以后想用平面几何的方法,那么可能会将二次曲线变换为圆更加方便,毕竟平面几何中对于圆的研究更加深入.

mathe

而关于上面的命题2，我们还可以有几种不同形式的变种
命题2.1,给定一个圆锥曲线$Gamma_1$及其上面一点$A_1$和外面一点$B_1$以及圆锥曲线$Gamma_2$及其上面一点$A_2$和外面一点$B_2$,存在射影变换，将$Gamma_1$变换为$Gamma_2$,$A_1$变换为$A_2$,$B_1$变换为$B_2$.
这个证明很简单，过$B_i$做$Gamma_i$的两切线得到两切点$C_i,D_i$,于是我们对$Gamma_i,A_i,C_i,D_i$使用命题2就可以了。
同样，上面的外面一点可以改为内部一点，而这个要稍微麻烦一些，
设直线$A_iB_i$交$Gamma_i$于另外一点$C_i$,过$C_i$的切线和过$A_i$的切线交于$D_i$,直线$B_iD_i$交$Gamma_i$于$E_i$,那么给定$Gamma_i,A_i,E_i$可以唯一确定$B_i$的位置，于是我们可以对$Gamma_i,A_i,C_i,E_i$采用命题2即可。

而根据命题2.1,我们还可以有一下推论
命题2.1.1,给定一个圆锥曲线$Gamma_1$及其上面一点$A_1$和里面一点$B_1$以及圆锥曲线$Gamma_2$及其上面一点$A_2$和里面一点$B_2$,存在射影变换，将$Gamma_1$变换为$Gamma_2$,$A_1$变换为$A_2$,$B_1$变换为$B_2$.

如下图，给定圆锥曲线上面一点A和内部一点B, AB连线交圆锥曲线于另外一点D,A和D点切线相交于E, BE和圆锥曲线交于F点。

那么对于命题2.1.1中的两条圆锥曲线，我们可以对应做出$E_1,F_1$和$E_2,F_2$点。然后根据命题2.1我们可以做出一个射影变换将$Gamma_1$变换到$Gamma_2$，$E_1$变换到$E_2$, $F_1$变换到$F_2$. 于是切线也有对应关系，所以$A_1$变换到$A_2$, $D_1$变换到$D_2$, 于是$A_1D_1$和$E_1F_1$的交点$B_1$映射到$B_2$.也就是这个变换满足要求。

mathe

而关于三次曲线，我了解的不多，只知道通过投影变换，任何三次曲线可以转化为标准形式$y^2=x^3+px+q$
而这类曲线的非退化形式被称为椭圆曲线，是现代数学中一个非常重要的概念，被非常广泛的研究过

余下还有一个对偶命题的概念也非常有用，这个下次再介绍