- 注册时间
- 2009-5-22
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 38780
- 在线时间
- 小时
|
 发表于 2010-2-9 16:58:32
|
显示全部楼层
发表于 2010-2-9 16:58:32
|
显示全部楼层
当年,我还真的认认真真的积分的一遍呢,能得到相同的结果的。
为什么要算呢,也是因为不相信这么巧。赫赫。
后来学了高斯定律,才发现其中的巧妙。
在后来学了场论,就觉得这个很自然了。
简单的说就是:
三维 ...
zgg___ 发表于 2010-2-8 11:57  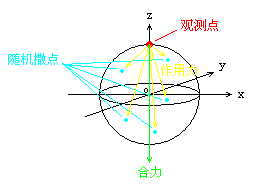 撒的点越多,计算出来的合力就与真实的重力越接近。
程序代码如下:
撒的点越多,计算出来的合力就与真实的重力越接近。
程序代码如下:- #include<cstdio>
- #include<cstdlib>
- #include<cmath>
-
- double fx,fy,fz,x,y,z,d2,d,f,r,m,G;
- unsigned int points;
-
- double random() //产生一个(-r,r)内的随机实数
- {
- return((rand()<<15)+rand()+0.5)/84.2678661-r;
- }
-
- int main()
- {
- r=6371004; //球体半径(m)
- m=5.972e+24; //球体质量(kg)
- G=6.6699e-11; //万有引力常数(m^3/(kg*s^2))
- /*
- 球心坐标: (0,0,0)
- 观测点坐标: (0,0,6371004)
- 观测点质量(kg): 1
- */
- while(1) //死循环,手动停止运行
- {
- x=random(); //在(±r,±r,±r)的立方体区域内随机撒点
- y=random(); //在(±r,±r,±r)的立方体区域内随机撒点
- z=random(); //在(±r,±r,±r)的立方体区域内随机撒点
- if(x*x+y*y+z*z<r*r) //如果该点在球体内部
- {
- points++; //计数
- d2=x*x+y*y+(z-r)*(z-r); //计算该点与观测点之间的距离的二次方
- d=sqrt(d2); //计算该点与观测点之间的距离
- f=G*m/d2; //计算观测点受该点的作用力大小
- fx+=f*x/d; //累加x方向作用力
- fy+=f*y/d; //累加y方向作用力
- fz+=f*(z-r)/d; //累加z方向作用力
- if(!(points&(points-1))) //如果撒点数量为2的幂
- printf("%d points:\nfx=%lf\nfy=%lf\nfz=%lf\n\n",points,fx/points,fy/points,fz/points); //输出作用力的累加结果
- }
- }
- return 0;
- }
|
|