当n=？时，含9的项之和开始大于不含9的项之和

G-Spider

当我用不超过100ms的时间解决了，用时要14s 的这个问题的时候，我泪流满面!!!!!!!

G-Spider

公式编辑器不太熟，还是百度贴吧的形式吧。
上面的情形对S9的情形处理的很好了。通过用欧拉公式，我想没有比这更好的了。只降到了3秒的运行时间，不错。但我还是不太满意，今天上课的时间突然想起了这事，也就思考了一下，发现还有潜力。
并且很优美。
当然是对不含9的情形，是不是觉得n=8,n=9时计算其仍然要不少的时间呢，所以从这里动刀，看能否将这两项的不含9的计算时间砍到0。
我首先想到的仍然是欧拉公式，这个的确没得说。细看#89楼的search_x()系列的循环，觉得可以用欧拉公式，并且很一致。
想法：
当n,m均较大时，有估计式：ln(n) - ln(m)=1/n  +1/(n-1)    +   ... +1/(m-1)
比如：对于n=8时的情形有：
search_8()
=(ln10000008 - ln9999999)  + (ln10000018 -ln10000009) + ...+ (ln88888888 -ln 88888879)
=ln(10000008/9999999)  + ln(10000018/10000009)   +  ... + ln(88888888/88888879)
=ln(1+9/9999999) + ln(1+9/10000009) +.... +ln(1+9/88888879)
到这里，你一定会有想法了，呵呵。没错，我们知道当x趋于0时，有估计式：ln (1+x) =x
好了，问题得到了简化：
=9/9999999 +9/10000009 + .... + 9/88888879
=9* (1/9999999+1/10000009+... +1/88888879)
是不是有点爽，发现这样一来，分母每次增量变成了10，几乎节省了一个数量级的除法次数。
但不太妙，这还是不好算啊，你很快会想到精度要求不太高的情形下，1/9999999=1/10000000于是有:
=9* (1/10000000+1/10000010 + ... +1/88888880)
嗯，不错了，.....，不是说了分母是以10为增量吗？所以有
=0.9 * (1/1000000 +10000001 +... + 1/88888888)
到此你有何感想，我反正想到了：
=0.9 * search_7()

所以要算：s0[9]和s0[8]，只要算一次search_7()
s0[8]=0.9*search_7();    //如果精度不太高的要求，还可以往前推（比如推到search6需要75ms）。
s0[9]=0.9*s0[8] ;     
---------------------------------------------------------
注意：不要用ln(10000008 /10000000)来估计ln(10000008/9999999)   这样本身就有误差，还会传递给ln(1+x)=x，误差更大。
---------------------------------------------------------
差不多了，我也没什么更好的办法了,此事，我可以安心结束了。

1. #include <stdio.h>
   
2. #include <time.h>
   
3. 
   
4. void disp(double s0,double s9,int n)
   
5. {
   
6.     printf( "s0[%d] = %.6f\ns9[%d] = %.6f\ns0/s9 = %.6f\n\n\n", n,s0,n,s9,s0/s9);
   
7. }
   
8. 
   
9. double calcS(int n)//n=1,2,3,...,
   
10. {
    
11.     int e[10]={1,10,100,1000,10000,100000,1000000,10000000,100000000,1000000000};
    
12.     int k;
    
13.     double s=0.0;
    
14.     for(k=e[n-1];k<e[n];k++)
    
15.         s+=1.0/k;
    
16.     return s;
    
17. }
    
18. 
    
19. //------------------------------
    
20. double search_1()
    
21. {
    
22.     double s9,s0=0.0;
    
23.     int k;
    
24.     for (k=1;k<=8;k++)
    
25.         s0+=1.0/k;
    
26.     return s0;
    
27. 
    
28. }
    
29. 
    
30. double search_2()
    
31. {
    
32.     double s9,s0=0.0;
    
33.     int a,b,k=10;
    
34.     for (b=1;b<=8;b++,k+=1)
    
35.         for (a=0;a<=8;a++,k++)
    
36.             s0+=1.0/k;
    
37.     return s0;
    
38. 
    
39. }
    
40. 
    
41. double search_3()
    
42. {
    
43.     double s9,s0=0.0;
    
44.     int a,b,c,k=100;
    
45.     for (c=1;c<=8;c++,k+=10)
    
46.         for (b=0;b<=8;b++,k+=1)
    
47.             for (a=0;a<=8;a++,k++)
    
48.                 s0+=1.0/k;
    
49.     return s0;
    
50. 
    
51. }
    
52. 
    
53. double search_4()
    
54. {
    
55.     double s9,s0=0.0;
    
56.     int a,b,c,d,k=1000;
    
57.     for (d=1;d<=8;d++,k+=100)
    
58.         for (c=0;c<=8;c++,k+=10)
    
59.             for (b=0;b<=8;b++,k+=1)
    
60.                 for (a=0;a<=8;a++,k++)
    
61.                     s0+=1.0/k;
    
62.     return s0;
    
63. 
    
64. }
    
65. 
    
66. double search_5()
    
67. {
    
68.     double s9,s0=0.0;
    
69.     int a,b,c,d,e,k=10000;
    
70.     for (e=1;e<=8;e++,k+=1000)
    
71.         for (d=0;d<=8;d++,k+=100)
    
72.             for (c=0;c<=8;c++,k+=10)
    
73.                 for (b=0;b<=8;b++,k+=1)
    
74.                     for (a=0;a<=8;a++,k++)
    
75.                         s0+=1.0/k;
    
76.     return s0;
    
77. 
    
78. }
    
79. 
    
80. double search_6()
    
81. {
    
82.     double s9,s0=0.0;
    
83.     int a,b,c,d,e,f,k=100000;
    
84.     for (f=1;f<=8;f++,k+=10000)
    
85.         for (e=0;e<=8;e++,k+=1000)
    
86.             for (d=0;d<=8;d++,k+=100)
    
87.                 for (c=0;c<=8;c++,k+=10)
    
88.                     for (b=0;b<=8;b++,k+=1)
    
89.                         for (a=0;a<=8;a++,k++)
    
90.                             s0+=1.0/k;
    
91.     return s0;
    
92. 
    
93. }
    
94. 
    
95. double search_7()
    
96. {
    
97.     double s9,s0=0.0;
    
98.     int a,b,c,d,e,f,g,k=1000000;
    
99.     for (g=1;g<=8;g++,k+=100000)
    
100.         for (f=0;f<=8;f++,k+=10000)
     
101.             for (e=0;e<=8;e++,k+=1000)
     
102.                 for (d=0;d<=8;d++,k+=100)
     
103.                     for (c=0;c<=8;c++,k+=10)
     
104.                         for (b=0;b<=8;b++,k+=1)
     
105.                             for (a=0;a<=8;a++,k++)
     
106.                                 s0+=1.0/k;
     
107.      return s0;
     
108. 
     
109. }
     
110. //下面的可以省了哦，^_^，哈哈
     
111. //---------------------------
     
112. /*double search_8()
     
113. {
     
114.     double s9,s0=0.0;
     
115.     int a,b,c,d,e,f,g,h,k=10000000;
     
116.     for (h=1;h<=8;h++,k+=1000000)
     
117.         for (g=0;g<=8;g++,k+=100000)
     
118.             for (f=0;f<=8;f++,k+=10000)
     
119.                 for (e=0;e<=8;e++,k+=1000)
     
120.                     for (d=0;d<=8;d++,k+=100)
     
121.                         for (c=0;c<=8;c++,k+=10)
     
122.                             for (b=0;b<=8;b++,k+=1)
     
123.                                 for (a=0;a<=8;a++,k++)
     
124.                                     s0+=1.0/k;
     
125.    return s0;
     
126. 
     
127. }*/
     
128. 
     
129. /*double search_9()
     
130. {
     
131.     double s9,s0=0.0;
     
132.     int a,b,c,d,e,f,g,h,i,k=100000000;
     
133.     for (i=1;i<=8;i++,k+=10000000)
     
134.         for (h=0;h<=8;h++,k+=1000000)
     
135.             for (g=0;g<=8;g++,k+=100000)
     
136.                 for (f=0;f<=8;f++,k+=10000)
     
137.                     for (e=0;e<=8;e++,k+=1000)
     
138.                         for (d=0;d<=8;d++,k+=100)
     
139.                             for (c=0;c<=8;c++,k+=10)
     
140.                                 for (b=0;b<=8;b++,k+=1)
     
141.                                     for (a=0;a<=8;a++,k++)
     
142.                                         s0+=1.0/k;
     
143.    return s0;
     
144. 
     
145. }
     
146. */
     
147. //----------------------
     
148. int main()
     
149. {
     
150.     double  s0[10]={0};
     
151.     double  s9[10]={0};
     
152.     //由欧拉公式lim(1+1/2+...+1/n)=lnn+C  (n->无穷,c为常数)
     
153.     //从第n=8开始，n值以达到其极限的精度要求
     
154.     //完全可以用估计式ln( n/m )=1/n +1/(n-1)+...+1/(m+1)
     
155.     //这样明显减少计算时间
     
156.     double  s_8=2.3025851829940506340183244547094;
     
157.     double  s_9=2.3025851019940457335179917876844;
     
158. 
     
159.     double  t0=clock();
     
160. 
     
161.     s0[1]=search_1();
     
162.     s0[2]=search_2();
     
163.     s0[3]=search_3();
     
164.     s0[4]=search_4();
     
165.     s0[5]=search_5();
     
166.     s0[6]=search_6();
     
167.     s0[7]=search_7();//如果想得到更粗糙一点的近似值时，可以用s0[7]=0.9*s0[6];输出前几位
     
168.     s0[8]=0.9*s0[7];//search_8();
     
169.     s0[9]=0.9*s0[8];//search_9();
     
170.    
     
171. 
     
172.             
     
173.     s9[1]=calcS(1)-s0[1];
     
174.     disp(s0[1],s9[1],1);
     
175.     s9[2]=calcS(2)-s0[2];
     
176.     disp(s0[2],s9[2],2);  
     
177.     s9[3]=calcS(3)-s0[3];
     
178.     disp(s0[3],s9[3],3);
     
179.     s9[4]=calcS(4)-s0[4];
     
180.     disp(s0[4],s9[4],4);
     
181.     s9[5]=calcS(5)-s0[5];
     
182.     disp(s0[5],s9[5],5);  
     
183.     s9[6]=calcS(6)-s0[6];
     
184.     disp(s0[6],s9[6],6);
     
185.     s9[7]=calcS(7)-s0[7];
     
186.     disp(s0[7],s9[7],7);            
     
187.     //==================     
     
188.     s9[8]=s_8-s0[8];
     
189.     disp(s0[8],s9[8],8);
     
190.     s9[9]=s_9-s0[9];   
     
191.     disp(s0[9],s9[9],9);
     
192.             
     
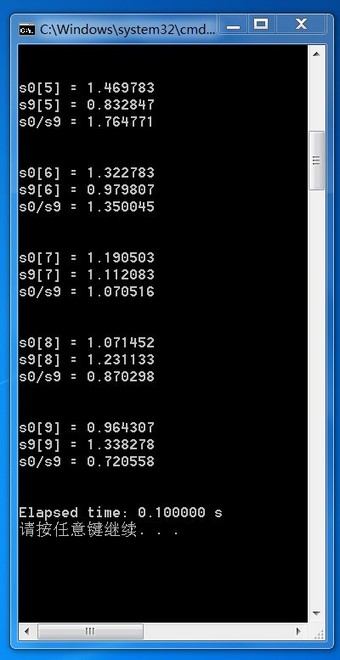
193.     printf("Elapsed time: %f s\n",(clock()-t0)/CLOCKS_PER_SEC);
     
194.     system("Pause");
     
195.     return 0;
     
196. }

复制代码

部分结果：

chyanog

92# G-Spider
\(^o^)/~，优化无极限啊。看截图你的win7 DPI比较高

chyanog

又写了两个Mathematica版，第一个算9位的需要比较大的内存（2G内存不够）；第二个接近了C的速度，算法和86楼的一致，不同的是只算不含9的数，如果把86楼的calcS去掉（这样也只算不含9的），速度几乎一致，注意：需要Mathematica8或以上版本且有Mathematica能识别的C编译器

1. f[n_] := 1/N@Flatten@Outer[Plus, ##] & @@ Array[10^(n - #) Range[Boole[# == 1], 8] &, n] // Tr;
   
2. h[n_] := H[10^n - 1.0] - H[10^(n - 1) - 1.0] /. H -> HarmonicNumber
   
3. Table[{Framed@n, h@n - #, #} &@f@n, {n, 8}] // Grid // AbsoluteTiming

复制代码

1. len = 9;
   
2. f1[n_] :=  Array[{Unique["x"], Boole[# == 1], 8} &, n] /.
   
3.       it_ :> {1/FromDigits[First /@ it], it} /. {e_, {it__}} :> Hold@Sum[e, it]
   
4. 
   
5. cf = Join @@ Table[f1[n], {n, len}] /.
   
6.      Hold[x__] :>   Compile[{}, {x}, RuntimeOptions -> "Speed",  CompilationTarget -> "C"];
   
7. 
   
8. h[n_] := H[10^n - 1.0] - H[10^(n - 1) - 1.0] /. H -> HarmonicNumber
   
9. 
   
10. MapIndexed[{Framed @@ #2, #} &,  Thread@{Array[h, len] - #, #} &@cf[]] // Grid // AbsoluteTiming
    

复制代码