六边形幻方

hujunhua

前面讨论了填入数为Range[1,19]  和Range[-9,9]的解。这个2层六边形幻方还可以填入其它的连续整数吗？

为了便于一般性讨论，记填入数为{a-9, a-8, ..., a-1, a, a+1, ..., a+8, a+9} , 于是幻方常数为19a/5. 必要条件是a=5k.
k=2, a=10时就是亚当斯的唯一珍品，k=0, a=0就是我们前面讨论的零和幻方。
k=1, a=5时为Range[-4,14]={-4,-3,-2,-1,0,1,2,3,4,5,6,7,8,9,10,11,12,13,14}, 经过编程搜索，这种情况存在37个本原解。下图是其中一例：

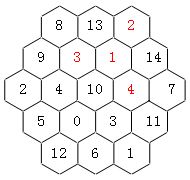可以证明，除了k=-2,-1,0,1,2, 对于k取其它的整数所得的连续数段，都不能用于填充这个2层六边形幻方。证明如下：
记内层6数之和为b, 中心数为c, 易得 b+2c=19k,
由于b>=(a-9)+(a-8)+...+(a-4)=6a-39=30k-39, 所以c<=(39-11k)/2
又c>=a-9=5k-9, 故5k-9<=(39-11k)/2, 得k<=2.

hujunhua