老封8853的视频号里面关于四圆的一个结论

hejoseph

以下结论能否推广到一般的四个圆？

$\odot O$、$\odot O_1$、$\odot O_2$、$\odot O_3$ 内切于点 $P$，半径分别为 $r$、$r_1$、$r_2$、$r_3$，当 $\frac{1}{r_1}+\frac{1}{r_2}+\frac{1}{r_3}-\frac{1}{r}=\frac{2\sqrt{r}}{\sqrt{r_1r_2r_3}}$ 时，存在 $\odot O$ 的一族动态内接三角形，使其三边总分别与 $\odot O_1$、$\odot O_2$、$\odot O_3$ 相切。

mathe

这个问题显然是二次对合变换的一种特例情况。
这些公切点的圆构成一族二次曲线系，所以它们对应的二次对合变换是可以交换的。总可以选择适当的组合，使得它们变换的复合是恒等变换，只是这里选择了三个变换的组合。
另外由于这些变换是可以交换的，这表明上面动态三角形和三边的相切关系可以任意选择，结果都是封闭的。
我们还可以改三角形为四边形，五边形，都可以找到。

mathe

我们可以设P为原点，各圆心在y轴上，于是对应圆的方程为
\(x^2+y^2-2ry=0\)
对应系数矩阵为
\(\begin{bmatrix}1&0&0\\0&1&-r\\0&-r &0\end{bmatrix}\)
于是\(r_1\)对应的变换的矩阵为
\(\begin{bmatrix}1&0&0\\0&1&-r\\0&-r &0\end{bmatrix}^{-1}\begin{bmatrix}1&0&0\\0&1&-r_1\\0&-r_1 &0\end{bmatrix}\)
对应特征方程为
\((x-1)(x-\frac{r_1}{r})^2=x^3 + \frac{-r - 2r_1}{r}x^2 + \frac{2r_1 r + r_1^2}{r^2}x - \frac{r_1^2}{r^2}\)
根据 https://emathgroup.github.io/blog/quadratic-convolution， 我们可以记\(u_2=\frac{r + 2r_1}{r}, u_1= \frac{2r_1 r + r_1^2}{r^2},u_0=\frac{r_1^2}{r^2}\)
那么这个变换对应的是退化椭圆曲线\(y^2=u_0(x^3+u_2x^2+u_1x+u_0)\)上点的横坐标。

mathe

由于我们可以把各变换曲线写成\(h(x^2+y^2-2ry)+(1-h)(x^2+y^2-2r_1y)=0\)
其中\(r_1\)参数对应曲线本身对应\(h_1=0\), \(r_2\)参数对应的曲线h使得\(rh+(1-h)r_1=r_2\)即\(h_2=\frac{r_2-r_1}{r-r_1}\), 同理\(h_3=\frac{r_3-r_1}{r-r_1}\)
而三个变换和形成恒等变换对应于这个三个h作为横坐标的点在这个退化椭圆曲线上三点共线。
设过三点直线方程为y=kx+b, 显然\(b=u_0\),代入椭圆曲线方程得到
\((kx+u_0)^2=u_0(x^3+u_2x^2+u_1x+u_0)\),即
\(u_0x^3+(u_0u_2-k^2)x^2+(u_0u_1-2ku_0)x=0\)

于是根据韦达定理我们可以得到
\(\begin{cases}k^2-u_0u_2=u_0(\frac{r_3-r_1}{r-r_1}+\frac{r_2-r_1}{r-r_1})\\
u_1-2k=\frac{r_3-r_1}{r-r_1}\frac{r_2-r_1}{r-r_1}\end{cases}\)
消去k就应该可以得到各r之间关系

hejoseph

谢谢！最上面那个结论我是用反演经过比较复杂的计算得到的，一般情况看来没什么简单的结论。

mathe

最简单的推广是把四个相切于同一点的圆推广为四个同根轴的圆,而圆相交的情况就变成具有两个公共交点的四个圆

数学星空

根据楼上4#的结果，我尝试算了一下：

\(k^2-u_0u_2=u_0(\frac{r_3-r_1}{r-r_1}+\frac{r_2-r_1}{r-r_1})\)

\(u_1-2k=\frac{r_3-r_1}{r-r_1}\frac{r_2-r_1}{r-r_1}\)

及\(u_0=\frac{r_1^2}{r^2},u_1=\frac{2rr_1+r_1^2}{r^2},u_2=\frac{r+2r_1}{r}\)

消元得到：

\(4r_1r_2r_3r^5 + (-4r_1^3r_2 - 4r_1^3r_3 - r_1^2r_2^2 - 10r_1^2r_2r_3 - r_1^2r_3^2 + 2r_1r_2^2r_3 + 2r_1r_2r_3^2 - r_2^2r_3^2)r^4 + 4r_1^4(r_1 + 3r_2 + 3r_3)r^3 - 2r_1^4(6r_1^2 + 3r_1r_2 + 3r_1r_3 - r_2r_3)r^2 + 8r_1^7r - r_1^8=0\)

而\(\frac{2\sqrt{r}}{\sqrt{r_1r_2r_3}}=\frac{1}{r_1}+\frac{1}{r_2}+\frac{1}{r_3}-\frac{1}{r}\)

去根号并展开有：

\(4r^3r_1r_2r_3 + (-r_1^2r_2^2 - 2r_1^2r_2r_3 - r_1^2r_3^2 - 2r_1r_2^2r_3 - 2r_1r_2r_3^2 - r_2^2r_3^2)r^2 + (2r_1^2r_2^2r_3 + 2r_1^2r_2r_3^2 + 2r_1r_2^2r_3^2)r - r_1^2r_2^2r_3^2=0\)

显然不一致？

mathe

看到问题所在了，链接里的描述方式是如果目标曲线为J, 原变换曲线为K, 那么参数h对应的曲线为hJ+K, 我这里弄成hJ+(1-h)K了，这个需要修正一下

mathe

由于我们需要把其它曲线写成
\(h(x^2+y^2-2ry)+(x^2+y^2-2r_1y)=0\)
也就是\(x^2+y^2-2\frac{rh+r_1}{1+h}y=0\)
所以我们得到
\(r_2=\frac{rh_2+r_1}{1+h_2}\)
得到\(h_2=\frac{r_2-r_1}{r-r_2},h_3=\frac{r_3-r_1}{r-r_3}\)
代入
\(\begin{cases}k=\frac{u_1-h_2h_3}2\\
k^2-u_0u_2-u_0(h_2+h_3)=0
\end{cases}\)
后，可以得到约束方程
-4*r3*r2*r1*r^5 + ((r2^2 + 10*r3*r2 + r3^2)*r1^2 + (2*r3*r2^2 + 2*r3^2*r2)*r1 + r3^2*r2^2)*r^4 + ((-2*r2^2 - 8*r3*r2 - 2*r3^2)*r1^3 + (-6*r3*r2^2 - 6*r3^2*r2)*r1^2 - 4*r3^2*r2^2*r1)*r^3 + ((r2^2 + 2*r3*r2 + r3^2)*r1^4 + (6*r3*r2^2 + 6*r3^2*r2)*r1^3 + 6*r3^2*r2^2*r1^2)*r^2 + ((-2*r3*r2^2 - 2*r3^2*r2)*r1^4 - 4*r3^2*r2^2*r1^3)*r + r3^2*r2^2*r1^4=0
展开后和楼主表达式只相差\((r-r_1)^2=0\),由于\(r\neq r_1\),所以两者等价

mathe

现在我们可以换一个圆系，选择所有经过(-1,0),(1,0)两个点的圆，可以假设它们圆心在点\((0,c_i),i=0,1,2,3\)
于是对应方程为\(x^2+y^2-2c_iy-1=0\),写成矩阵形式为
\(M_i=\begin{bmatrix}1&0&0\\0&1&-c_i\\0&-c_i&-1\end{bmatrix}\)
计算\(M_0^{-1}M_1\)的特征多项式后得到
\(u_2=\frac{c_0^2+2c_1c_0+3}{c_0^2+1}, u_1=\frac{2c_1c_0+c_1^2+3}{c_0^2+1},u_0=\frac{c_1^2+1}{c_0^2+1}\)
同样设\(h_1=0\), 由于\(h_i (x^2+y^2-2c_0y-1)+(x^2+y^2-2c_1y-1)=(h_i+1)(x^2+y^2-2c_iy-1); i=2,3\)
我们同样得到\(h_2=\frac{c_2-c_1}{c_0-c_2},h_3=\frac{c_3-c_1}{c_0-c_3}\)
于是得到它们形成三角形的条件为
-4*c0^6 + ((-4*c3*c2 + 12)*c1 + (4*c2 + 4*c3))*c0^5 + ((c2^2 + 10*c3*c2 + (c3^2 - 12))*c1^2 + (2*c3*c2^2 + (2*c3^2 - 14)*c2 - 14*c3)*c1 + (c3^2*c2^2 - 6*c3*c2 - 3))*c0^4 + ((-2*c2^2 - 8*c3*c2 + (-2*c3^2 + 4))*c1^3 + (-6*c3*c2^2 + (-6*c3^2 + 18)*c2 + 18*c3)*c1^2 + ((-4*c3^2 + 2)*c2^2 + 16*c3*c2 + (2*c3^2 + 8))*c1 + (2*c3*c2^2 + (2*c3^2 + 2)*c2 + 2*c3))*c0^3 + ((c2^2 + 2*c3*c2 + c3^2)*c1^4 + (6*c3*c2^2 + (6*c3^2 - 10)*c2 - 10*c3)*c1^3 + ((6*c3^2 - 4)*c2^2 - 16*c3*c2 + (-4*c3^2 - 6))*c1^2 + (-6*c3*c2^2 + (-6*c3^2 - 6)*c2 - 6*c3)*c1 + (c2^2 - 2*c3*c2 + c3^2))*c0^2 + ((-2*c3*c2^2 + (-2*c3^2 + 2)*c2 + 2*c3)*c1^4 + ((-4*c3^2 + 2)*c2^2 + 8*c3*c2 + 2*c3^2)*c1^3 + (6*c3*c2^2 + (6*c3^2 + 6)*c2 + 6*c3)*c1^2 + (-2*c2^2 + 4*c3*c2 - 2*c3^2)*c1)*c0 + ((c3^2*c2^2 - 2*c3*c2 + 1)*c1^4 + (-2*c3*c2^2 + (-2*c3^2 - 2)*c2 - 2*c3)*c1^3 + (c2^2 - 2*c3*c2 + c3^2)*c1^2)=0.
特别的，如果目标圆以(-1,0),(1,0)为直径，对应\(c_0=0\)时，约束条件变成
\((c_1c_2c_3)^2-2c_1c_2c_3(c_1+c_2+c_3)+(c_1^2+c_2^2+c_3^2)-2(c_1c_2+c_2c_3+c_3c_1)=0\)
比如我们选择\(c_1=1,c_2=\frac13,c_3=4-\sqrt{15}\), 对应图片
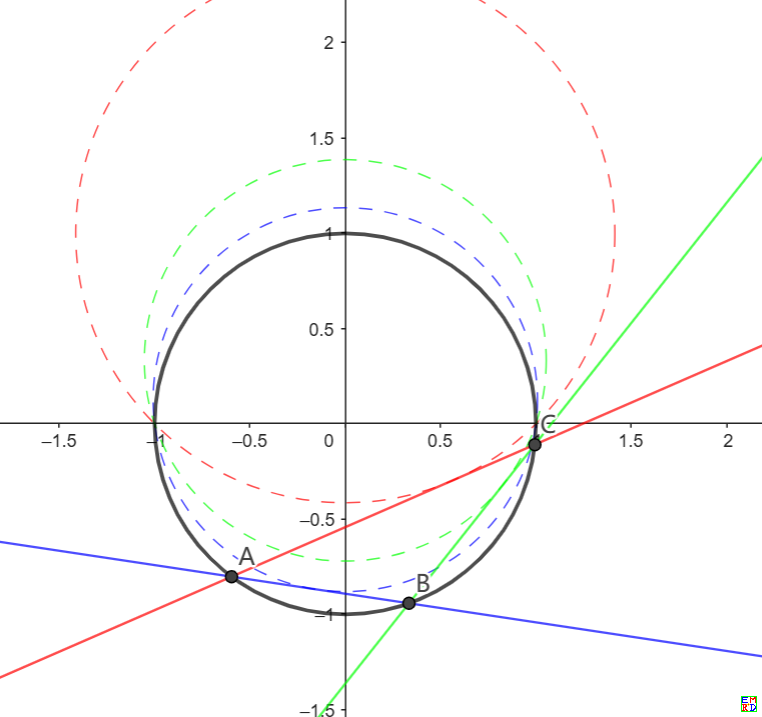