求半圆的半径？

nyy · 发表于 4 天前

马上注册，结交更多好友，享用更多功能，让你轻松玩转社区。

您需要登录才可以下载或查看，没有账号？欢迎注册

×

求半圆的半径？

aimisiyou · 发表于 4 天前

解方程组。

nyy · 发表于 4 天前

aimisiyou 发表于 2025-9-22 09:32
解方程组。

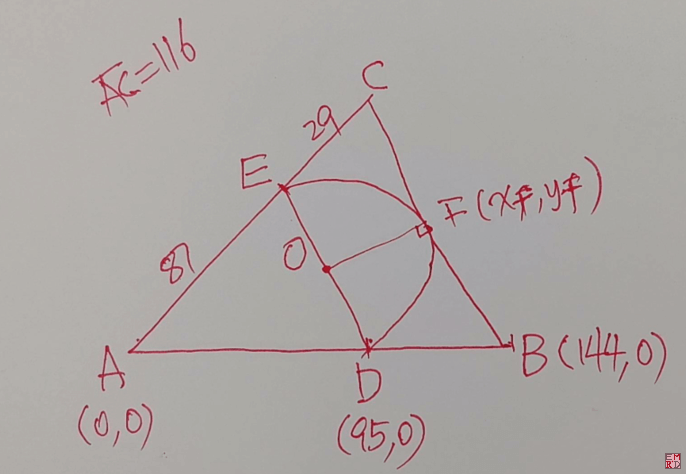
Clear["Global`*"];(*mathematica11.2,win7(64bit)Clear all variables*)
(*解析几何求解问题*)
(*点坐标初始赋值*)
{xa,ya}={0,0};
{xd,yd}={95,0};
{xb,yb}={144,0};
(*用万能公式替换掉余弦正弦,这样可以避免三角函数,t表示角的一半的正切值*)
{xe,ye}=89*{(1-t^2)/(1+t^2),2*t/(1+t^2)}
{xc,yc}=(89+29)*{(1-t^2)/(1+t^2),2*t/(1+t^2)}
(*得到中点坐标,也就是圆心*)
{xo,yo}=({xe,ye}+{xd,yd})/2
(*计算OF,BC的斜率*)
kOF=(yf-yo)/(xf-xo)
kBC=(yb-yc)/(xb-xc)
(*列方程组解决问题*)
ans=Solve[{
Numerator@Together[kOF*kBC-(-1)]==0,(*OF与BC垂直,所以斜率乘积等于-1*)
EuclideanDistance[{xo,yo},{xe,ye}]==EuclideanDistance[{xo,yo},{xf,yf}]==R,(*OE=OF=半径R*)
Det[{{xc,yc,1},{xf,yf,1},{xb,yb,1}}]==0(*CFB三点共线*)
},{xf,yf,t,R}]//FullSimplify//ToRadicals
aaa=Select[ans,And[xf>=0,yf>=0]/.#&](*删选出F点坐标在第一象限的*)
Grid[aaa,Alignment->Left](*列表显示*)
Grid[N[aaa,10],Alignment->Left](*列表显示*)
BC=EuclideanDistance[{xc,yc},{xb,yb}]/.aaa//FullSimplify//ToRadicals(*计算BC的长度*)

复制代码

方程组求解结果
\[\begin{array}{llll}
\text{xf}\to \frac{83779304167861-93165912 \sqrt{4762038090}}{838751391179} & \text{yf}\to \frac{1652 \sqrt{\frac{3}{113} \left(981684965115430363-14066369454466 \sqrt{4762038090}\right)}}{7422578683} & t\to \frac{13}{2} \sqrt{\frac{3}{14 \sqrt{4762038090}+966899}} & R\to 2 \sqrt{\frac{3 \left(8302546067-118370 \sqrt{4762038090}\right)}{168457801}} \\
\text{xf}\to \frac{93165912 \sqrt{4762038090}+83779304167861}{838751391179} & \text{yf}\to \frac{1652 \left(236397921 \sqrt{3422}+10085747 \sqrt{1391595}\right)}{838751391179} & t\to \frac{21 \sqrt{3422}+\sqrt{1391595}}{6026} & R\to 2 \sqrt{\frac{3 \left(118370 \sqrt{4762038090}+8302546067\right)}{168457801}} \\
\end{array}\]

数值化
\[\begin{array}{llll}
\text{xf}\to 92.22059869 & \text{yf}\to 3.803350794 & t\to 0.008097623365 & R\to 3.091014513 \\
\text{xf}\to 107.5508832 & \text{yf}\to 50.67079647 & t\to 0.3996206400 & R\to 34.25347213 \\
\end{array}\]

BC长度
\[\left\{2 \sqrt{\frac{225649786897-2854656 \sqrt{4762038090}}{168457801}},2 \sqrt{\frac{2854656 \sqrt{4762038090}+225649786897}{168457801}}\right\}\]

BC数值化
{26.085560599246717687, 100.17769332104894027}

nyy · 发表于 4 天前

nyy 发表于 2025-9-22 10:10
方程组求解结果
\[\begin{array}{llll}
\text{xf}\to \frac{83779304167861-93165912 \sqrt{476203809 ...

Clear["Global`*"];(*mathematica11.2,win7(64bit)Clear all variables*)
(*子函数,利用三边计算角的余弦值,角是c边所对的角*)
cs[a_,b_,c_]:=((a^2+b^2-c^2)/(2*a*b))
(*线段长度变量赋值*)
AD=DA=95;DB=BD=49;
AE=EA=87;EC=CE=29;
AO=OA=a;BO=OB=b;CO=OC=c;
BF=FB=d;FC=CF=e;
DO=OD=EO=OE=FO=OF=R;
ans=NSolve[{
cs[OD,OA,AD]+cs[OE,OA,AE]==0,
cs[DA,DO,AO]+cs[DB,DO,BO]==0,
cs[FB,FO,BO]==0,
cs[FC,FO,CO]==0,
cs[EO,EC,OC]+cs[EA,EO,AO]==0,
cs[AD,AE,BO+OE]==cs[AD+DB,AE+EC,BF+FC],
a>=0&&b>=0&&c>=0&&d>=0&&e>=0&&R>=0
},{a,b,c,d,e,R}]

复制代码

这段代码，我感觉写的没问题，就是不知道为什么求解不出结果！

nyy · 发表于 4 天前

nyy 发表于 2025-9-22 10:10
方程组求解结果
\[\begin{array}{llll}
\text{xf}\to \frac{83779304167861-93165912 \sqrt{476203809 ...

上面的代码输入有错误，长度应该是87，而不是89

Clear["Global`*"];(*mathematica11.2,win7(64bit)Clear all variables*)
(*解析几何求解问题*)
(*点坐标初始赋值*)
{xa,ya}={0,0};
{xd,yd}={95,0};
{xb,yb}={95+49,0};
(*用万能公式替换掉余弦正弦,这样可以避免三角函数,t表示角的一半的正切值*)
{xe,ye}=87*{(1-t^2)/(1+t^2),2*t/(1+t^2)}
{xc,yc}=(87+29)*{(1-t^2)/(1+t^2),2*t/(1+t^2)}
(*得到中点坐标,也就是圆心*)
{xo,yo}=({xe,ye}+{xd,yd})/2
(*计算OF,BC的斜率*)
kOF=(yf-yo)/(xf-xo)
kBC=(yb-yc)/(xb-xc)
(*列方程组解决问题*)
ans=Solve[{
Numerator@Together[kOF*kBC-(-1)]==0,(*OF与BC垂直,所以斜率乘积等于-1*)
EuclideanDistance[{xo,yo},{xe,ye}]==EuclideanDistance[{xo,yo},{xf,yf}]==R,(*OE=OF=半径R*)
Det[{{xc,yc,1},{xf,yf,1},{xb,yb,1}}]==0(*CFB三点共线*)
},{xf,yf,t,R}]//FullSimplify//ToRadicals
aaa=Select[ans,And[xf>=0,yf>=0]/.#&](*删选出F点坐标在第一象限的*)
Grid[aaa,Alignment->Left](*列表显示*)
Grid[N[aaa,10],Alignment->Left](*列表显示*)
BC=EuclideanDistance[{xc,yc},{xb,yb}]/.aaa//FullSimplify//ToRadicals(*计算BC的长度*)

复制代码

求解结果
\[\begin{array}{llll}
\text{xf}\to \frac{531}{5} & \text{yf}\to \frac{252}{5} & t\to \frac{2}{5} & R\to 34 \\
\text{xf}\to \frac{1530351}{16745} & \text{yf}\to \frac{86268}{16745} & t\to \frac{2}{169} & R\to 26 \sqrt{\frac{5}{197}} \\
\end{array}\]

数值化
\[\begin{array}{llll}
\text{xf}\to 106.2000000 & \text{yf}\to 50.40000000 & t\to 0.4000000000 & R\to 34.00000000 \\
\text{xf}\to 91.39151986 & \text{yf}\to 5.151866229 & t\to 0.01183431953 & R\to 4.142144421 \\
\end{array}\]

BC长度
\[\left\{100,\frac{884}{\sqrt{985}}\right\}\]
数值化
{100.000000000000000000000000000,28.1665820641707426641508211048}

nyy · 发表于 4 天前

nyy 发表于 2025-9-22 10:21
上面的代码输入有错误，长度应该是87，而不是89

小圆的情况是切点在延长线上，
大圆的情况是图中的情况。

nyy · 发表于 4 天前

nyy 发表于 2025-9-22 10:21
上面的代码输入有错误，长度应该是87，而不是89

Clear["Global`*"];(*mathematica11.2,win7(64bit)Clear all variables*)
(*解析几何求解问题*)
(*点坐标初始赋值*)
{xa,ya}={0,0};
{xd,yd}={95,0};
{xb,yb}={95+49,0};
{xe,ye}=87/(87+29)*{xc,yc}
(*得到中点坐标,也就是圆心*)
{xo,yo}=({xe,ye}+{xd,yd})/2
(*计算OF,BC的斜率*)
kOF=(yf-yo)/(xf-xo)
kBC=(yb-yc)/(xb-xc)
(*列方程组解决问题*)
ans=Solve[{
xc^2+yc^2==(87+29)^2,(*AC=87+29*)
Numerator@Together[kOF*kBC-(-1)]==0,(*OF与BC垂直,所以斜率乘积等于-1*)
EuclideanDistance[{xo,yo},{xe,ye}]==EuclideanDistance[{xo,yo},{xf,yf}]==R,(*OE=OF=半径R*)
Det[{{xc,yc,1},{xf,yf,1},{xb,yb,1}}]==0(*CFB三点共线*)
},{xc,yc,xf,yf,R}]//FullSimplify//ToRadicals
aaa=Select[ans,And[xf>=0,yf>=0]/.#&](*删选出F点坐标在第一象限的*)
Grid[aaa,Alignment->Left](*列表显示*)
Grid[N[aaa,10],Alignment->Left](*列表显示*)
BC=EuclideanDistance[{xc,yc},{xb,yb}]/.aaa//FullSimplify//ToRadicals(*计算BC的长度*)

复制代码

代码稍微修改也能得到结果

王守恩 · 发表于 3 天前

你必须学会用三角函数。

Solve[{116/Sin[b] == 144/Sin[c], (2 R)^2 == (49 Sin[b] + 29 Sin[c])^2 == 95^2 +87^2 + 2*95*87 Cos[b + c], Pi/2 > c > b > 0, R > 0}, {b, c, R}]

{{b -> 2 ArcTan[1/2], c -> 2 ArcTan[8/9], R -> 34}}

nyy · 发表于 3 天前

王守恩发表于 2025-9-23 09:24
你必须学会用三角函数。

Solve[{116/Sin == 144/Sin[c], (2 R)^2 == (49 Sin + 29 Sin[c])^2 == 95^2 +87^ ...

我看了一下思路应该行得通

王守恩 · 发表于 3 天前

角度比长度更重要。

Solve[{116/Sin[b] == 144/Sin[c], (2 R)/Sin[b + c] == 95/Cos[2 a - c], (2 R)/Sin[Pi/2] == w/Sin[a] == z/Cos[a], 49/Sin[a] == w /Sin[b] == y/Sin[a + b],
29/Cos[a] == z/Sin[c] == x /Cos[c - a], Pi/2 > a > 0, Pi > c > b > 0, x > 0}, {a, b, c, R, x, y, z, w}] // FullSimplify

{{a -> 2 ArcTan[1/7 (-6 + Sqrt[85])], b -> 2 ArcCot[2], c -> 2 ArcTan[8/9], R -> 34, x -> 37, y -> 63, z -> 24 Sqrt[17/5], w -> 28 Sqrt[17/5]}}

账号		自动登录	找回密码
密码			欢迎注册

[提问] 求半圆的半径？

马上注册，结交更多好友，享用更多功能，让你轻松玩转社区。

点评

点评