求正方形的面积

nyy

王守恩 发表于 2025-12-9 11:52
Solve[{13/Sin[c] == 11/Sin == (2 y)/Sin[c + b], 6/Cos[a] == Sqrt[x]/Sin, 2/Sin[a] == y/Sin[a + c] == ...

1. Clear["Global`*"];(*mathematica11.2,win7(64bit)Clear all variables*)
   
2. deg=Pi/180;(*角度制下1°所对应的弧度*)
   
3. (*子函数,利用三边计算角的余弦值,角是c边所对的角*)
   
4. cs[a_,b_,c_]:=((a^2+b^2-c^2)/(2*a*b))
   
5. rule={
   
6.     eq1->(cs[a,x,6]^2+cs[a,x,2]^2==1),(*两角相加等于90°,则余弦值的平方和等于1*)
   
7.     eq2->(ArcCos@cs[6,a,x]+ArcCos@cs[Sqrt[2]*a,7,9]==135deg)(*两个角相加等于180-45=135°*)
   
8. }
   
9. (*画等值线图,可以发现有两个大于零的实数解*)
   
10. ContourPlot[{cs[a,x,6]^2+cs[a,x,2]^2==1,
    
11.              ArcCos@cs[6,a,x]+ArcCos@cs[Sqrt[2]*a,7,9]==135deg},{a,-10,10},{x,-10,10}]
    
12. (*得到第一组解,这组解似乎有一个是钝角*)
    
13. aa=FindRoot[{eq1,eq2}/.rule,{{a,4.0},{x,4.0}},WorkingPrecision->30]
    
14. bb=RootApproximant[{a,x}/.aa]
    
15. (*得到第二组解*)
    
16. cc=FindRoot[{eq1,eq2}/.rule,{{a,6.0},{x,6.0}},WorkingPrecision->30]
    
17. dd=RootApproximant[{a,x}/.cc]
    

复制代码

求解结果
{a -> 3.06785995538948174803904543879,
x -> 3.78852757367167491958002577397}

{4 Sqrt[10/17], 2 Sqrt[61/17]}

{a -> 5.21536192416211897166637724594,
x -> 5.44058820349417733801197494882}

{2 Sqrt[34/5], 2 Sqrt[37/5]}

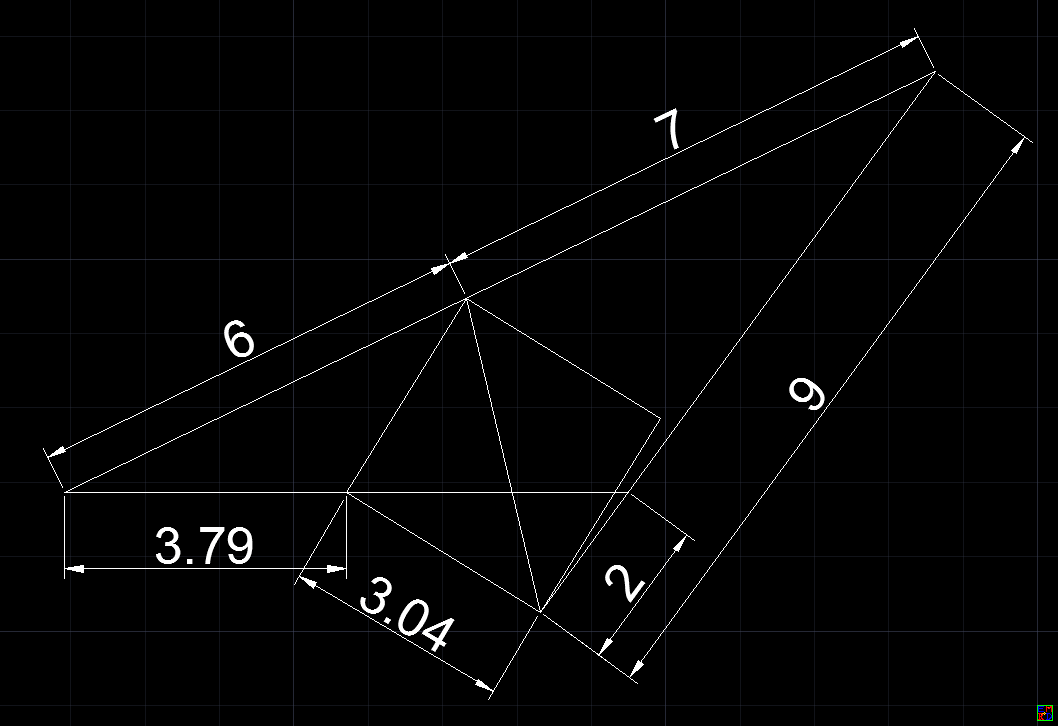
第一组解所对应的图形。

nyy

nyy 发表于 2025-12-9 14:09
求解结果
{a -> 3.06785995538948174803904543879,
x -> 3.78852757367167491958002577397}

由于软件求解方程组的解恨困难，没办法只好用牛顿迭代法先得到高精度数值解，然后再得到精确解

王守恩

记  \(7=k_{1},6= k_{2},9=k_{3},2=k_{4},\)    题意不变。

正方形面积  =  \(\D\frac{(k_{1} k_{4} + k_{2} k_{3}) (k_{1}^2 - k_{2}^2 - k_{3}^2 + k_{4}^2)}{4 (k_{1} k_{4} - k_{2} k_{3})}\)

nyy

nyy 发表于 2025-12-9 14:09
求解结果
{a -> 3.06785995538948174803904543879,
x -> 3.78852757367167491958002577397}

还是方程组牛逼！
把增根都能搞出来