在圆周上任意取3点，求这3个点可以被分配在一个半圆周上的概率

kastin

kastin 发表于 2014-1-9 21:51
可以用正n边形来逼近圆。考虑n个顶点的情况。正n边心是中心对称的，所以其中某个点A的选取认为是已经确 ...

嗯嗯，我看漏了一个数字。这种方法到底哪里有漏洞呢？

kastin

3楼中关于$p(x)$的求解处稍微省略了一些，出现了点纰漏，下面重新给出完整过程：

1. (弦中点在直径上均匀分布) 下面来求概率密度函数$p(x)$。先求出分布函数$F(x)$，根据分布函数的定义，弦长小于或者等于$x$的概率即为$F(x)$。由于圆内弦长被其中心唯一确定，弦长只跟它与圆心的距离有关，而与方向无关。那么弦长小于或者等于 $x$ 的弦与圆心距离$d$肯定满足$dger=sqrt{1-(x//2)^2}$，我们有$F(x)=(1-r)/1$，所以概率密度函数$$p(x)=\frac{\text{d}F(x)}{\text{d}x}=-\frac{\text{d}r}{\text{d}x}=\frac{x}{2\sqrt{4-x^2}}$$于是所求概率为$$\int_0^1p(x)(1-\frac{\arcsin\frac{x}{2}}{\pi})\text{d}x=\frac{\pi-1}{\pi}$$.

2. (弦中点在半径为$r$的圆周上均匀分布) 根据情况1，长度为 $x$ 的弦的中点肯定落在半径 $r$ 的圆周上，那么弦长小于或等于$x$的弦的中点定是在一个圆环内（单位圆挖去半径为$r$的圆），那么$F(x)=1-(\pi\cdotr^2)/(\pi\cdot1^2)=1-r^2$故概率密度函数$$p(x)=\frac{\text{d}F(x)}{\text{d}x}=-\frac{2r\text{d}r}{\text{d}x}=\frac{x}{2}$$所求概率为$$\int_0^1p(x)(1-\frac{\arcsin\frac{x}{2}}{\pi})\text{d}x=\frac{3}{4}$$

hujunhua

kastin 发表于 2014-1-9 21:51
可以用正n边形来逼近圆。考虑n个顶点的情况。正n边心是中心对称的，所以其中某个点A的选取认为是已经确 ...

由于连续的圆周上总是存在对径点的，所以不妨取n为偶数，就设n=2m吧。使用正多边形逼近时用5#的方法最合适不过了。
1、总的三角形数目是$C_n^3$，是3次多项式. 我们来分别计数，看其中有多少锐角三角形、直角三角形和钝角三角形。
2、直角三角形的数目是n(m-1), 是二次多项式，在取n->∞的极限时可以忽略不计。
3、钝角三角形和锐角三角形的顶点不包含成对的对径点，所以对径点总是2取1的。可以在三角形之间定义一种关联：
      将一个三角形的一个顶点换成对径点所得的三角形称为原三角形的一个关联三角形。显然，每个非直角三角形都有3个关联三角形。
容易知道，一个锐角三角形的3个关联三角形都是钝角三角形，而一个钝角三角形的3个关联三角形包括1个锐角三角形和2个钝角三角形。
可见一个锐角三角形的3个关联钝角三角形不与别的锐角三角形关联，由于关联是相互的，每个钝角三角形都是一个锐角三角形的三个关联三角形之一。
所以锐角三角形与钝角三角形的数量之比为1：3. 故忽略直角三角形，取到钝角三角形的概率为3/4.

kastin

后来把思路给整理了一下，你们看看有没有问题：

先来扯一点背景。
我们知道，历史上第二次数学危机就是计算过程涉及到无穷这个概念的，微积分的严密性依赖于无穷计算。对于这个路，前人们走得很艰辛曲折，直到完善的今天。凡是涉及到无穷个，或者无穷大量，无穷小量的计算问题，必须谨慎对待，因为这与普通有限运算是不一样的。

一个集合的势就是该集合内部元素的个数，对于有限个元素构成的集合来说，它的势是一个有限值；但是对于无穷集，就不那么简单了。很简单的例子，自然数集$N={1,2,3,...}$（0是不是自然数在学术界有争议，我们这里就不将0算入在内），那么它的势$|N|=\aleph_0$, 这是基数无穷。根据康托的对应方法，奇数的个数与偶数的个数是一样的，并且都等于自然数的个数。当然比这个无穷还大的有更多，比如整数的个数。

同样，可以知道，任何一段线段上的点的个数是无穷多个的，但是你不能说长度较长的线段中，点的个数（无穷个）一定比长度短的线段中点的个数（也是一个无穷）要多。因为总可以用一个线性映射将这两段线段内的点一一对应，所以它们所含的点的个数是在这种定义下是一样多的（虽然都是无穷多个）。对于面积图形也是类似的。这里可以看出集合的势的大小跟“势”的定义有关。如果集合内的元素是可数的（可测的），那么必然有一种一一映射关系，将集合的元素映射为一个可数的集合，且这两个集合是等势的。通过映射来进行无穷集合的势的定义。显然，不同定义方式，得到的结果不同。

楼主的问题中，由于是在一个圆周上取点（广义的情况是在超球面上取），那么这些点的个数是无穷多个的，同样只在某段圆弧上取点，也是无穷多个的。根据上文描述，这个圆弧段内的点是与圆周上的点可以通过某种映射一一对应，所以如果给出某种取点方式，就能保证在圆弧段上和圆周上取点是等价的，如何证明你的取点方式一定就是整个圆周上的点呢？如何操作，使得选中每个点的概率是一样的呢？因此定义清楚“任取”的概念，有助于解决问题。若记进行一次圆周上“任取”三个点的试验为一个样本，那么所有可能的样本能构成一个集合（总体）H，可知这个集合的势是无穷大的。同样，满足问题要求（三个点能分配在半圆周上）的样本是总体H的一个子集S，而这个子集的势也是无穷大的。这里的圆弧段看成是圆周的子集，且都是无穷集。如果样本之间是等概率的，根据古典概率论，所求的概率就是$|S|/|H|$(无穷大比上无穷大)。那么这个结果是多少呢？根据上一段的解释，这跟集合的势的定义有关，即测度的问题。长度，面积概念的来源就是为了区分这种几何元素构成的不同无穷集之间的区别的。要知道，拉普拉斯，伯努利，帕斯卡等人构建的概率学是古典概率，事件“等概率”发生也是明确无误的，样本集是可测的。现代概率论则是建立在集合论上，有着严密的公理基础的。

现在回到问题，我们重新一步一步分析。

问题：
圆周上任取三个点，那么这三个点可以被分配子啊一个半圆周上的概率是多少？
注:这个问题可以等价为这句话“圆周上任取三点，能共线，或者共点，或者能构成钝角三角形（直角三角形也算在内）的概率是多少？”（千万不要遗漏了“能共线，或者共点”的退化情况，因为这些特殊情况的个数也是无穷多个的。）

分析：
前面已经详细说明了，“任取”这个概念必须定义清楚。一般来说，“任取”这个词有两层含义：1. 三个点的选取过程相互独立（因此三个点之间可以存在重叠的情况）；2. 选点的方式是“等概率”的。 第一层没问题，关键在于第二层的定义。因为点的个数是无穷多个的，所以这里得很小心。我这里可以举几个例子来说明：

我们可以构造如下几种“等概率”取点方式：
a. (点在圆弧上均匀分布) 这种方法基于“长度”这个测度。单位圆上随便定一个点为起始点，记$s$为逆时针方向圆弧上任意一点到起始点的弧长。由于半径是1，所以$s$的取值范围为$[0, 2\pi)$。显然，$s$的取值与圆周上的点是一一对应的。只要给定一个$s$取值，就能找到确定位置的唯一一点。因此，若随机取点方式定义为：点在圆弧上按照长度概念的均匀分布。那么$s$就是是区间$[0, 2\pi)$上服从均匀分布的一个随机变量，于是无论s在该区间内取什么值，其概率密度均为1/(2\pi)。即取圆周上任意一点的概率密度为1/(2\pi)。

b. (点的方向在平面内均匀分布) 这种方法是基于“角度”这个测度的。下面你会发现这种定义方式的结果跟方案a一样（因为半径是1，如果半径不是1，那就不一样了）。取圆周上一点P并与圆心O连结，作为参考方向。$OY$为单位圆的圆心发射出的一条射线，参考方向OP逆时针选择到OY的角度（弧度制）记作$\alpha$，那么$\alpha$取值范围为$[0, 2\pi)$。该区间内任意一个给定的$alpha$对应一条射线，射线与圆周的交点就是选取的点，因此$\alpha$与圆周上的点是一一对应的。 若定义随机取点的方式为：点与圆心连线的方向在圆平面内均匀分布。那么$\alpha$是在$[0, 2\pi)$上均匀分布的一个随机变量，取任何值的概率密度均相同，且为$1/(2\pi)$。

c. (面积均匀) 问题是在平面中的，那么平面系统内所有测度中的“长度”，"弧度"已经用过了，还剩下“面积”。仿照上述方案，可构造一种取点方案：在单位圆内等概率任取一点（概率密度为$1/(\pi\cdot1^2)=1/(2\pi)$），取得该点后从圆心向该点发射射线并与圆周相交，交点即为我们要选取的点。但是这种方法存在一个问题——圆周上的点和圆内部的点不是一一对应的，而是一对多。所以我们将上述取点方案定义进行修改：由于圆内的点唯一确定了一条弦垂直于该点到圆心的连线。因此，圆内的一个点就对应圆周上的两个点。然后以$1/2$的概率从弦的两个端点中选取一个即可。这就能圆周上保证任何一个点被选取的概率是相同的。有人也许会认为圆内的点取在圆心的时候，弦不是唯一的。的确如此，但是我们总是按照固定方向取其中一条弦，而剩下过圆心的那些弦的两个端点，根据上面改进的选点方式，会被其他不过圆心的弦所包含进去了，且是等概率选中的。这就保证了一一对应且等概率。所以选中的概率密度为$1/2\times1/(\pi\cdot1^2)=1/(2\pi)$（同样是因为半径为1，所以结果与a,b方案相同）

d. (直径上均匀) 类似地，方案c是采用弦来构造一一对应。同样我们可以在单位圆的任意一条直径上等概率取点，并作垂直于该直径的弦，弦的两个端点中等概率选择即可。直径上的点等概率选择的概率密度为$1/(2\times1)$，然后通过该点作一条垂直于所给直径的弦，弦的两个端点按照$1/2$概率选取，于是圆周上的点均能等概率被选中。概率密度为$1/2\times1/2=1/4$。

需要说明的是，不同方案的选择，对于问题最后的结果有可能是相同的。

hujunhua和wayne等人给出的方法中，本质上就已经默认了随机取点方式为上述b方案。

至此，对于随机取点方式我们已经有了明确的理解了。只要给出合法的选点方式，那么问题才能进一步被解决。

kastin

现在考虑三点在半圆周上的情况。这些情况有无穷多种，因此需要构建一种一一对应，来计算这种集合的势。然后考虑三元组（三个点）集合的势，二者之比即为所求概率。

现在根据上面提到的三种选点方案，分别分析如下：
a, b, c由于点的选取是按照随机变量在$[0,2\pi)$上确定的，所以三个随机变量(x,y,z)都是$[0,2\pi)$上均匀分布。总共的空间应该是$[0,2\pi)^3$，测度为$|H|=8\pi^3$。找出满足条件的集合，计算出测度$|S_t|, t\in{a,b,c}$. 那么问题最终答案应该是$|S_t|/(8\pi^3)$。方案d则是：$|S_d|/(4^3)$。则是然而这个方式有些复杂，我们可以转换一下思路来求解。

假设三个点A,B,C是依次等概率随机选取，那么必然是先A后B再C。一旦AB确定，那么要构成满足ABC在半圆周上（钝角三角形或退化情况）只取决于C的位置。

AB一旦确定，那么弦$bar{AB}$的长度自然就确定了，假设长度为$l$。记随机取三个点中的前两点构成的弦长为$l$的概率是$p(l)$，已知两点距离为$l$的前提下，第三点满足题目要求的概率为$p_c(l)$. 因此按照全概率公式，ABC三点满足题目要求的概率为$$P=\int_0^2p(l)p_c(l)\text{d}l$$其中，等式右端第二项是条件概率。

下面来分别尝试给出$p(l)$和$p_c(l)$。
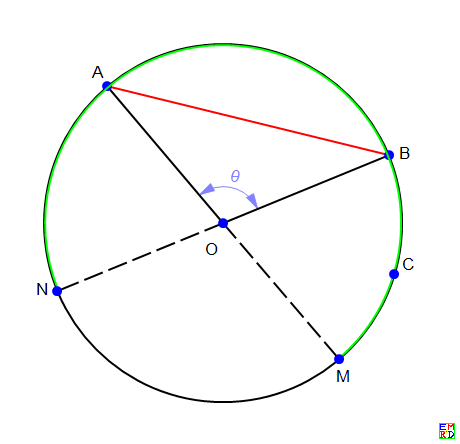
方案a和b：在圆的情况下，这两种方案本质是一样的，我们这里仅仅考察b。由于点在各个方向是均匀分布的，所以当OA的方位角与OB的方位角之差$\theta$（弦AB的圆心角)在平面内也是在$[0,2\pi)$内均匀变化的的，故弦长为$l$时概率$$p(l)=\frac{\arcsin \frac{l}{2}}{\pi}$$ 将A,B分别与圆心O连线并延长，与圆交于M,N两点。那么当C落在弧MBAN上时（图中绿色弧段上），就能确保ABC三点在半圆周上。由于C在各个方向上是均匀的分布的，所以$$p_c(l)=1-\frac{\arcsin \frac{l}{2}}{\pi}$$ 根据上面的全概率公式可以计算出，这两种方案下问题的答案是$$\int_0^2\frac{\arcsin \frac{l}{2}}{\pi}(1-\frac{\arcsin \frac{l}{2}}{\pi})\text{d}l=\frac{8-4\pi+\pi^2}{2\pi^2}\approx0.268665$$

方案ab的配图

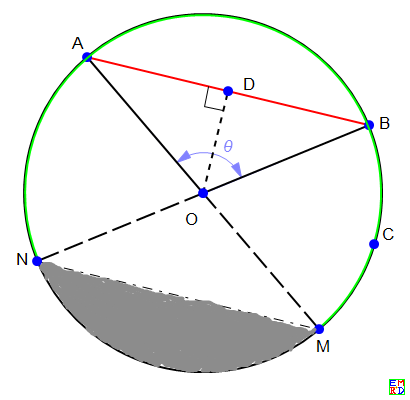
方案c：这种情况下用的是面积测度。所以$p(l), p_c(l)$的求解是根据面积比率得出。类似我在12楼过程，$r=|OD|=\sqrt{1-(l//2)^2}$, $$p(l)=-\frac{2r\text{d}r}{\text{d}l}=\frac{l}{2}$$但是$p_c(l)$就不再是$1-1/\pi\arcsin \frac{l}{2}$了，因为这里用的是面积（即弦中心在圆内部的分布）。类似a,b中的方法，将A,B分别连接圆心O并延长，各自与圆相交于M,N点。那么当C点所在的弦的中点在弦MN与弧MN构成的弓形区域（下图中灰色部分）之外时，能保证等概率得到C在绿色弧段上。因此$$p_c(l)=1-S_{弓形}/S_圆=1-\frac{\arcsin \frac{l}{2}-\frac{l}{2}\sqrt{1-(\frac{l}{2})^2}}{\pi}$$ 于是可以求出积分$$\int_0^2\frac{l}{2}(1-\frac{\arcsin \frac{l}{2}-\frac{l}{2}\sqrt{1-(\frac{l}{2})^2}}{\pi})\text{d}l=\frac{7}{8}$$

方案c的配图

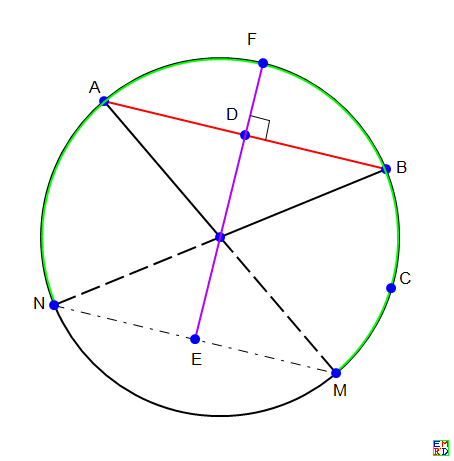
方案d：类似方案c的方法，$$p(l)=\frac{\text{d}F(l)}{\text{d}l}=-\frac{\text{d}r}{\text{d}l}=\frac{l}{2\sqrt{4-l^2}}$$而c点所在弦的中点必须在紫色线段上，因而有$$p_c(l)=\frac{1-r}{2}=\frac{1-\sqrt{1-(l/2)^2}}{2}$$ 于是最后结果为$$\int_0^2\frac{l}{2\sqrt{4-l^2}}\frac{1-\sqrt{1-(l/2)^2}}{2}\text{d}l=\frac{1}{4}$$

wayne

kastin 发表于 2014-1-10 12:14
后来把思路给整理了一下，你们看看有没有问题：

先来扯一点背景。

你这里的概率密度 好像有 偷梁换柱之嫌： 概率密度不等于 概率，应该不能简单的相乘吧。

kastin

wayne 发表于 2014-1-15 16:16
你这里的概率密度 好像有 偷梁换柱之嫌： 概率密度不等于 概率，应该不能简单的相乘吧。

额，是我的疏忽。方案a,b中定义式那里有点问题。应该是\[F(l)=\frac{\arcsin \frac{l}{2}}{\pi}\]而\[p(l)=\frac{\text{d}F}{\text{d}l}\frac{1}{\pi\sqrt{4-l^2}}\]
同样，对应的\(p_c(l)\)也应该改成\[1-\frac{1}{\pi\sqrt{4-l^2}}\]积分就得重新算了。
下面的方案c中的\[p_c(l)=1-S_{弓形}/S_圆=1-\frac{\arcsin \frac{l}{2}-\frac{l}{2}\sqrt{1-(\frac{l}{2})^2}}{\pi}\]也需要求一次导数，然后再代入积分。

wayne

另外，方案d的计算似乎值得推敲：
首先有一个共识。问题明确的说了，是在圆周上任意取三个点。
换句话来解读，就是点在其自由运动的轨迹(即圆周)上是等概率分布的。
所以取点方式不管怎样，圆周上任取一点，其概率是${d\theta}/{2\pi}$,概率密度函数是$1/{2\pi}，\theta \in [0,2\pi]$。
（如果要用集合的势来解释，微元即是0，于是任取一点的概率是0，刚好符合情理）


既然方案d这个取点方式计算答案不一致，我们可以单独讨论一下。我的计算方法是：
在圆内随机取一个直径线段，由于直径是线段，在径向上是没有方向的，那么取得一个确定的直径，其概率是 ${d\theta}/{\pi}$，概率密度函数是 $1/{\pi}$, $\theta \in [0,\pi]$
取得一个直径之后，随意做一个垂直于直径的弦，其概率是 ${dL}/2$，弦总是能与圆周交于两个点，如果任取其一，那么将会重复计算点,点的分布不是在整个圆周均匀,而是沿着直径方向是均匀的.这与题干所说的任意性不符合.
所以,我们规定直径的右手法则的一侧作为取点的法则.。 所以圆周上取一点 的概率就是  ${d\theta}/{\pi} *{dL}/2$ ，于是其概率密度就是 $\1/{2*\pi}$ ,对应的微元就是$d\thetad\L$

此处的概率密度 ${d\theta*dL}/{2\pi}, \theta \in [0,\pi], L \in [0,2]$ 跟前面的$1/{2\pi}d\theta, \theta \in [0,2\pi]$ 在数量上是不具有可比性的。

mathe

圆周上随机取n个点，落在半圆上概率可以如下计算。
对于任意t,$0<t<=1/2$,我们设n个点落在角度不超过$t*2pi$上概率为$F_n(t)$,于是我们知道$F_2(t)=2t$
而且$F_{n+1}(t)=\int_{s=0}^t (2t-s)dF_n(s)$
然后$F_n(1/2)$就是所求的结果
比如
$F_3(t)=\int_{s=0}^t(4t-2s)ds=3t^2$,
$F_4(t)=\int_{s=0}^t(2t-s)*6sds=4t^3$
猜测$F_n(t)=nt^{n-1}$,于是$F_{n+1}(t)=\int_{s=0}^t (2t-s)*n*(n-1)s^{n-2}ds=\int_{s=0}^n(2n(n-1)ts^{n-2}-n(n-1)s^{n-1}ds=2nts^{n-1}-(n-1)s^n|_{s=0}^t=(n+1)t^n$,归纳假设成立
于是n个点落在半圆上概率为$n/{2^{n-1}}$

wayne

设 $X_i, 0\leq i \leq n$ 服从 $[0,2\pi]$的均匀分布.
那计算 $ P( max{X_1,X_2,....X_n} - min{X_1,X_2,....X_n} <\pi)$
得到 ${n+1}/2^n$