- 注册时间
- 2012-4-20
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 3497
- 在线时间
- 小时
|
 发表于 2021-10-10 14:53:15
|
显示全部楼层
发表于 2021-10-10 14:53:15
|
显示全部楼层
若是在几年前,我多半使用重心坐标来做,现在不会了
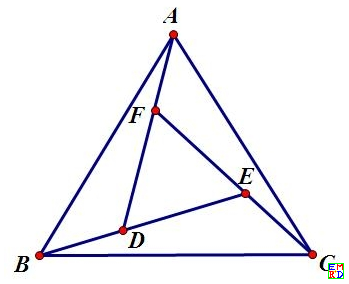
解:令
\[\mathop {BA}\limits^ \to = (x + yi)\mathop {BC}\limits^ \to \]
因为$S_{BCE}$是$S_{ABC}$的四分之一, 所以可令
\[\mathop {BE}\limits^ \to = (p + \frac{y}{4}i)\mathop {BC}\limits^ \to \]
$D$在$BE$上,令
\[\mathop {BD}\limits^ \to = \lambda \mathop {BE}\limits^ \to = \lambda (p + \frac{y}{4}i)\mathop {BC}\limits^ \to \]
$S_{DAB}$是$S_{ABC}$的四分之一, 分别计算
\[{\mathop{\rm Im}\nolimits} \frac{{D - A}}{{B - A}} = \frac{{\lambda (4p - x)y}}{{4({x^2} + {y^2})}}, \quad
{\mathop{\rm Im}\nolimits} \frac{{C - A}}{{B - A}} = \frac{y}{{{x^2} + {y^2}}}\]
前者应为后者的四分之一,故可解出
\[\lambda = \frac{1}{{4p - x}}\]
然后计算$AD$与$CE$的交点$F$:
\[\mathop {BF}\limits^ \to = \frac{{ - 12p + 16{p^2} + 4x - 20px + 4{x^2} + iy - 12ipy + 3ixy}}{{4(1 - 16p + 16{p^2} + 4x - 8px + {x^2})}}\mathop {BC}\limits^ \to \]
$S_{FCA}$是$S_{ABC}$的四分之一, 分别计算
\[{\mathop{\rm Im}\nolimits} \frac{{F - C}}{{A - C}} = \frac{{(3 - 4p + x)(1 - 12p + 3x)y}}{{4(1 - 16p + 16{p^2} + 4x - 8px + {x^2})(1 - 2x + {x^2} + {y^2})}} ,\quad
{\mathop{\rm Im}\nolimits} \frac{{B - C}}{{A - C}} = \frac{y}{{1 - 2x + {x^2} + {y^2}}} \]
前者为后者的四分之一,即得方程:
\[1 - 12p + 16{p^2} + 3x - 8px + {x^2} = 0\]
它有两个解:
\[p = \frac{1}{8}(3 - \sqrt 5 + 2x), \quad
p = \frac{1}{8}(3 + \sqrt 5 + 2x)\]
对应的各点表示分别为:
\[\mathop {BD}\limits^ \to = \frac{{3 - \sqrt 5 + 2x + 2iy}}{{4(3 - \sqrt 5 )}}\mathop {BC}\limits^ \to , \quad
\mathop {BE}\limits^ \to = \frac{1}{8}(3 - \sqrt 5 + 2x + 2iy)\mathop {BC}\limits^ \to , \quad
\mathop {BF}\limits^ \to = \frac{{2 + 7x - 3\sqrt 5 x + 7iy - 3i\sqrt 5 y}}{{4(3 - \sqrt 5 )}}\mathop {BC}\limits^ \to \]
\[\mathop {BD}\limits^ \to = \frac{{3 + \sqrt 5 + 2x + 2iy}}{{4(3 + \sqrt 5 )}}\mathop {BC}\limits^ \to , \quad
\mathop {BE}\limits^ \to = \frac{1}{8}(3 + \sqrt 5 + 2x + 2iy)\mathop {BC}\limits^ \to , \quad
\mathop {BF}\limits^ \to = \frac{{2 + 7x + 3\sqrt 5 x + 7iy + 3i\sqrt 5 y}}{{4(3 + \sqrt 5 )}}\mathop {BC}\limits^ \to \] |
|