一个概率游戏的最佳策略

lsr314

游戏只有一轮时，选b的人获胜的概率p是一个有断点的分段函数：
$b≤a时，p=1-a+ab,b>a时，p=(1-a)b.$
右边的函数值总是不大于左边，所以b从左边趋近于a时概率最大。
如果0≤a≤1/2,b选0就可以保证胜率≥1/2.
如果1/2≤a≤1,那么b=1/2时p=1-a/2≥1/2.
总结一下,为了保证获胜概率不小于1/2,b的策略有两种：
$如果a<1/2，那么b=0，如果a≥1/2,那么b=1/2.$
b的策略是建立在对a的判断上的，并不存在一个固定的b，使得不管a选几，b获胜的概率都不小于1/2.从这个意义上来说，双方并不存在楼主想要的最佳策略。这是一个类似石头剪刀布的游戏。

webcraft

可以确定没有楼主定义的这种最佳策略：“如果玩家2无论采取什么策略，玩家1的胜率均不低于50%，那么玩家1的策略就是最佳策略。”，因为如果有这种策略的话，两个人都采用这种策略，到底谁胜率高呢？这和自相矛盾的故事是一个道理。。

mathe

我们假设游戏结束后赢的人获得利润1，输的获得利润-1，于是这是一个零和游戏。
先考虑最后一轮的时候，假设两者现在相差$k$倍，不妨设$k>=1$,其中玩家1领先。显然在$k>=2$时，玩家1采用最保守策略必然可以赢得比赛，获得利润1。
所以我们主要看$1<=k<=2$的情况。
于是假设这时第一个玩家使用策略$a$,第二个玩家使用策略$b$,那么第二个玩家赢的概率为
$ Q(k,a,b)=[((2-b)>k(2-a))?ab:0] +[(2-b)(1+a)>k?(1-a)b:0]+[(1+a)>k(1+b)?(1-a)(1-b):0] $
如图三条彩色曲线代表上面三个不等式在a-b曲面上的图。双方博弈时，对于每个a的取值，如果和
某些边界相交，那么相当于要求对应处b的密度函数取值之间存在某些关系。

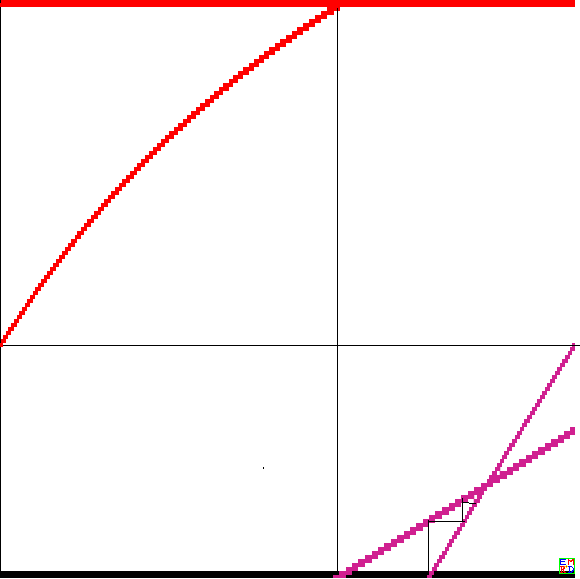
于是这种策略下，玩家1的利润的期望为$1-2Q(k,a,b)$,同样玩家2的利润的期望为$2Q(k,a,b)-1$
于是假设玩家2的最优策略的密度函数为g(b)，必然有$\int_{b=0}^1 (2Q(k,a,b)-1)g(b)db = 2\int_{b=0}^1Q(k,a,b)g(b)db-1$的取值和a无关(或者玩家1不使用a)
于是表达式$H(k,a)=\int_{b=0}^1Q(k,a,b)g(b)db=C$对于a求偏导必然为0.
由于
$H(k,a) = a\int_{b=0}^{max{0, 2-k(2-a)}} bg(b)db + (1-a)\int_{b=0}^{min{1, 2-k/{1+a}}} bg(b)db + (1-a)\int_{b=0}^{max{0,(1+a)/k-1}}(1-b)g(b)db = C$
由$2-k/(1+a)>0$,而且$1>=2-2/k>k-1>=0$
第一个积分非零的条件是$a>2-2/k$,第三个积分非零的条件是$a>k-1$
我们得出
\(H(k,a)=C=\begin{cases}a\int_{b=0}^{2-k(2-a)}bg(b)db + (1-a)\int_{b=0}^1 bg(b)db + (1-a)\int_{b=0}^{\frac{1+a}{k}-1}(1-b)g(b)db && 2-\frac{2}{k}\le a\le 1\\ \\ (1-a)\int_{b=0}^{\frac{1+a}{k}-1}(1-b)g(b)db+ (1-a)\int_{b=0}^1bg(b)db && k-1\le a\le 2-\frac{2}{k}\\  \\(1-a)\int_{b=0}^{2-\frac{k}{1+a}} bg(b)db && 0\le a\le k-1\end{cases}\)
于是根据第二部分条件可以得出$\int_{b=0}^{{1+a}/k-1}(1-b)g(b)db=C/{1-a}-C_2$,
变量替换得出$\int_{b=0}^x(1-b)g(b)db=C/{2-k-kx}-C_2$,所以$g(x)={Ck}/{(1-x)(2-k-kx)^2}$对于一切$x\in(0,3/k-2/{k^2}-1)$，
根据第三部分$a=k-1$代入得出$C_2=\int_{b=0}^1bg(b)db=C/{2-k}$，顺带$a=0$代入可以有$C=\int_0^{2-k}bg(b)db=C$
同样对于第三类的情况，选手2的对策是$\int_{b=0}^{2-k/{1+a}} bg(b)db=C/{1-a}$,变量替换得出$\int_{b=0}^xbg(b)db={C(2-x)}/{4-k-2x}$
同样求导可以得出$g(x)={k*C}/{x(4-k-2x)^2}$对于一切$x\in(2-k,1)$。

现在比较有意思的是，根据第二类和第三类我们分别可以确定$b\in(0,3/k-2/{k^2}-1)$和$b\in(2-k,1)$中$g(b)$表达式（只是还有待定参数)
现在我们查看第一类中$H(k,a)$的表达式，对于$a\in(2-2/k, 2-3/k-3/{k^2}+2/{k^3})$对应图中阶梯状黑线的两条竖线之间,其中$H(k,a)$中第一个积分表达式正好可以利用前面第二类出来的结果
而$H(k,a)$中第二部分我们已知$\int_{b=0}^1 bg(b)db=C/{2-k}$，由此可以利用最后一部分根据$H(k,a)$和$a$取值无关的条件求出$g(b)$更大范围的表达式，
这种方法可以确定$b\in(0,\bar{b}={2-k}/{k+1})$范围的g函数表达式，其中点$(\bar{a}=1-\bar{b},\bar{b})$是图中两彩色直线交叉点。同样如果已经确定$b\in({2-k}/k,2-k)$范围的函数g的表达式，继续可以使用第一个公式确定余下所有区间$(\bar{b},2-k)$的函数g的
表达式，现在唯一缺失的就是$b\in({2-k}/k,2-k)$部分的表达式，这个是不是表示我们有很多选择的自由度。到底是这个区间只能取零？还是我们可以任意定义这个区间的密度函数，然后就可以唯一确定$b\in({2-k}/{k+1}, {2-k}/k)$区间的密度函数了。
现在关键是虽然理论上我们已经可以计算出g在$(3/k-2/{k^2}-1,\bar{b})$上表达式，但是实际上结果过于复杂，无法写出。不过如果能够计算出$\int_0^{\bar{b}}bg(b)db$或$g(\bar{b})$,都可以有助于分析$(\bar{b},2-k)$区间的情况，还可以用于帮忙确定$C$的值。
我们可以获得的信息是将$a=\bar{a}$代入第一式可得$\bar{a}\int_0^{\bar{b}}bg(b)db+(1-\bar{a})C/{2-k}+(1-\bar{a})\int_0^{\bar{b}}(1-b)g(b)db=C$
同样如果将$a=\bar{a}$代入第一式的微分形式可以得到$(k+1/k)\bar{a}\bar{b}g(\bar{b})=C/{2-k}+\int_0^{\bar{b}}(1-b)g(b)db-\int_0^{\bar{b}}bg(b)db$

类似我们要对Q函数关于a积分对b求偏导数可以得出第一个玩家的策略函数，同样估计要分类计算，估计计算量也不会小，而且不一定能够有解析解。
然后再得出两个玩家的最有策略后，应该可以计算出他们的利润的期望值$P_1(k)$.
此后，理论上我们就可以计算第二轮对应的Q函数，然后继续类似上面过程就可以得出两个玩家的最佳策略和利润期望值函数...

mathe

上面边界条件应该弄错了，k=1时应该三个积分都参与是最复杂的情况

KeyTo9_Fans

当回合数$n=1$时，

把选数范围限制在$0.01$、$0.02$、$0.03$、……、$1.00$这$100$个数里面之后，

可以求得双方的最佳策略如下所示：

　　以$0.004248$的概率选$0.01$，
　　以$0.006222$的概率选$0.02$，
　　以$0.004548$的概率选$0.03$，
　　……
　　以$0.005895$的概率选$1.00$。

此时对方无论从这$100$个数里面选哪个数，胜率都恰好是$50%$。

以横坐标为所选的数，纵坐标为选取概率，作出的散点图如下所示：



把散点连起来，可以得到两条曲线，但是曲线的函数表达式看起来并不简单，我很难猜出准确的表达式。

mathe

$k=1$时$H(1,a) = a\int_{b=0}^a bg(b)db + (1-a)\int_{b=0}^1 bg(b)db + (1-a)\int_{b=0}^a(1-b)g(b)db$
$\frac{\partial H(1,a)}{\partial a}=\int_{b=0}^a bg(b)db+a^2g(a)-\int_{b=0}^1 bg(b)db-\int_{b=0}^a(1-b)g(b)db+(1-a)^2g(a)=0$这个是密度函数满足的方程。
设$G(x)=\int_0^x g(t)dt$,于是分部积分得到$\int_0^x tg(t)dt = xG(x)-\int_0^x G(t)dt$
设$J(x)=\int_0^x G(t)dt$,我们可以得出$\int_{b=0}^a bg(b)db=aG(a)-J(a)$,$\int_{b=0}^1 bg(b)db=G(1)-J(1)$, $\int_{b=0}^a (1-b)g(b)db=G(a)+J(a)-aG(a)$
于是我们得出方程$2aG(a)-2J(a)-G(a)+a^2g(a)+(1-a)^2g(a)-G(1)+J(1)=0$,其中$G(1)=1$
或者我们可以写成$J(x)$的二阶微分方程$(2x-1)J'(x)-2J(x)+(x^2+(1-x)^2)J''(x)-1+J(1)=0$
而这个微分方程的解的二阶导数就是两人最佳策略的密度函数

上面条件还可以改写为
$\int_{b=0}^a (2b-1)g(b)db+(2a^2-2a+1)g(a)=c=\int_{b=0}^1bg(b)db={\int_{b=0}^1(2b-1)g(b)db+1}/2$
设函数$K(a)=\int_{b=0}^a (2b-1)g(b)db$,于是$g(a)={K'(a)}/{2a-1}$,得出一阶微分方程$K(a)+{2a^2-2a+1}/{2a-1}K'(a)=K(a)+((a-1/2)+1/{4(a-1/2)})K'(a)=c={K(1)+1}/2$
可以看出$K(x)$关于$x=1/2$对称，于是可以设$K(x)=k_0+k_1(x-1/2)^2+k_2(x-1/2)^4+....$
由此我们可以得出$(2h+1)k_h+{(2h+2)k_{h+1}}/4=0, h>=1$,由此我们可以得出$K(x)$在$x=1/2$的泰勒展开式
$K(x)=u-v*(1-\frac{1!!}{2!!}(2x-1)^2+\frac{3!!}{4!!}(2x-1)^4-\frac{5!!}{6!!}(2x-1)^6+...)$,
而且容易看出收敛半径是$1/2$,只是在x靠近0或1时收敛速度很慢
$g(x)=2v*(\frac{1!!}{0!!}-\frac{3!!}{2!!}(2x-1)^2+\frac{5!!}{4!!}(2x-1)^4-...)$
而且$\int_{1/2}^x g(x)dx=(2x-1)(u-K(x))$。又因为$\int_{1/2}^1g(x)dx=1/2$所以$u=1/2$
然后根据$K(0)=0$,我们得出$1/2=v(1-\frac{1!!}{2!!}+\frac{3!!}{4!!}-\frac{5!!}{6!!}+...)$,根据数值计算可以猜测$1-\frac{1!!}{2!!}+\frac{3!!}{4!!}-\frac{5!!}{6!!}+...=1/{\sqrt{2}}$,
所以得出$v=1/{\sqrt{2}}$
得出$g(x)=\sqrt{2}(\frac{1!!}{0!!}-\frac{3!!}{2!!}(2x-1)^2+\frac{5!!}{4!!}(2x-1)^4-...)$
$g(x)$这个展开式在$x=0$附近完全无法计算，甚至我们无法得出$g(0)$
又因为$K(1)=K(0)=0$,所以我们有$K(a)+{2a^2-2a+1}/{2a-1}K'(a)=1/2$或者$K(a)+(2a^2-2a+1)g(a)=1/2$,所以$g(a)={1/2-K(a)}/{2a^2-2a+1}$,
由此应该有$g(1)=g(0)=1/2$,而且我们知道$g(1/2)=\sqrt{2}$，现在这个数据基本同Fans的数值计算结果相同了
当然这还是一个收敛极其缓慢的条件收敛序列，但是至少比$g(x)$要容易计算
或者我们可以试着将g(x)表示为连分式形式得出$g(x)=\sqrt{2}[0;3/2(2x-1)^2, -1/4(2x-1)^2, 5/12(2x-1)^2,1/12(2x-1)^2,7/20(2x-1)^2,3/20(2x-1)^2,9/28(2x-1)^2,5/28(2x-1)^2,...]={\sqrt{2}}/{1+{3/2(2x-1)^2}/{1-{1/4(2x-1)^2}/{1+{5/12(2x-1)^2}/{1+...}}}}$

zeroieme

3D图试验

只玩1回合是没有最佳策略的

1. Plot3D[#,{a,0,1},{b,0,1},ColorFunction->Function[{a,b},Switch[Sign[#],-1,Green,1,Red,0,Yellow]]]&[a*b*Sign[(2-a)-(2-b)]+(1-a)b*Sign[1/(1+a)-(2-b)]+a(1-b)Sign[(2-a)-1/(1+b)]+(1-a)(1-b)Sign[1/(1+a)-1/(1+b)]]

复制代码

而考虑n回合的最后1回合，假设两者已经存在w的金额比。当w超过1有最佳策略，是w的函数。

1. Plot3D[#,{a,0,1},{b,0,1},ColorFunction->Function[{a,b},Switch[Sign[#],-1,Green,1,Red,0,Yellow]]]&[a*b*Sign[(2-a)w-(2-b)]+(1-a)b*Sign[w/(1+a)-(2-b)]+a(1-b)Sign[(2-a)w-1/(1+b)]+(1-a)(1-b)Sign[w/(1+a)-1/(1+b)]/.w->1.3]

复制代码

KeyTo9_Fans

经双方选数范围为$0.0001$、$0.0002$、$0.0003$、……、$1.0000$共$10000$个数的实战验证，

发现$g(x)=2v\cdot(\frac{1!!}{0!!}-\frac{3!!}{2!!}(2x-1)^2+\frac{5!!}{4!!}(2x-1)^4-...)$完全正确！

但是$v=1$不对，应该是$v=\sqrt{2}/2$，

得出$g(x)=\sqrt{2}\cdot(\frac{1!!}{0!!}-\frac{3!!}{2!!}(2x-1)^2+\frac{5!!}{4!!}(2x-1)^4-...)$，

然后得出$g(0)=g(1)=1/2$是对的，

但是$g(1/2)$应该等于$\sqrt{2}$而不是$2$。

从$15$楼的图也能看出这些结果：

　　两条曲线的峰值的平均数应该是$0.014$而不是$0.02$，

　　两条曲线的边界的平均数是$0.005$没有错。

#####

还没等我写完这篇贴子，mathe已经偷偷地把他的贴子改过来了

mathe

根据16#连分数公式可以给出如下g(x)的图

mathe

13#中只给出了计算g(b)的方案过程，相对应的，我们还需要分析第一个用户的方案f(a),类似有
$L(k,b)=b\int_{min{2-{2-b}/k,1}}^1af(a)da+b\int_{max{0,k/{2-b}-1}}^1(1-a)f(a)da+(1-b)\int_{min{k(1+b)-1,1}}^1(1-a)f(a)da$
同样
在$0<=b<2/k-1$时
$L(k,b)=b\int_{2-{2-b}/k}^1af(a)da+b\int_0^1(1-a)f(a)da+(1-b)\int_{k(1+b)-1}^1(1-a)f(a)da$
而在$2/k-1<=b<2-k$时
$L(k,b)=b\int_{2-{2-b}/k}^1af(a)da+b\int_0^1(1-a)f(a)da$, 对应解$f(x)=C/{x(2-2k+kx)^2}$对于一切$x\in(2-3/k+2/{k^2},1)$
而在$2-k<=b<=1$时
$L(k,b)=b\int_{k/{2-b}-1}^1(1-a)f(a)da$,对应解$f(x)=C/{(1-x)(2x+2-k)^2}$对于一切$x\in(0,k-1)$