- 注册时间
- 2007-12-27
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 49484
- 在线时间
- 小时
|
楼主 |
发表于 2022-11-9 20:06:26
|
显示全部楼层
换了组数据做测试,验证了上面的方案可行,比如选择如下四组点,每组四个点:
[0,0,1],[1,0,1],[0,1,1],[1,1,1]
[2,2,1],[2,3,1],[3,2,1],[3,3,1]
[4,4,1],[4,5,1],[5,4,1],[6,6,1]
[10,10,1],[11,11,1],[10,11,1]
我们假设有虚点$(a+bi, c+di)$和它的共轭点同每组的四个点都六点共圆锥曲线,并且设d=br,可以得到方程:
(-4*r*c + 2*r)*a^2 + (-4*r^2*b^2 + (4*c^2 + (4*r - 4)*c - 2*r))*a + ((4*r*c + (2*r^2 - 2*r))*b^2 + (-2*c^2 + 2*c))=0
(4*r*c - 10*r)*a^2 + (4*r^2*b^2 + (-4*c^2 + (-20*r + 20)*c + (50*r - 24)))*a + ((-4*r*c + (-10*r^2 + 10*r))*b^2 + (10*c^2 + (24*r - 50)*c + (-60*r + 60)))=0
-4*r*a^3 + ((16*r + 4)*c + (-20*r - 16))*a^2 + ((-4*r^3 + 16*r^2 - 4*r)*b^2 + ((-4*r - 16)*c^2 + (-112*r + 112)*c + (360*r - 192)))*a + (((4*r^2 - 16*r + 4)*c + (16*r^3 - 92*r^2 + 92*r - 16))*b^2 + (4*c^3 + (16*r + 20)*c^2 + (192*r - 360)*c + (-864*r + 864)))=0
(4*r*c - 42*r)*a^2 + (4*r^2*b^2 + (-4*c^2 + (-84*r + 84)*c + (882*r - 440)))*a + ((-4*r*c + (-42*r^2 + 42*r))*b^2 + (42*c^2 + (440*r - 882)*c + (-4620*r + 4620)))=0
我们可以通过数值法(牛顿迭代)找到几组实数解,比如[a,b,c,r]=
[3.3977035170695895892746281275100215092, 1.2095696424892583832474261333152633094, -0.34126823285394525048749673328351439472, 1.5306621354683455615906467453926368480]
[6.6083150028155415386948182258750703195, -0.024275721798213817304471274955574804557, 6.6083150028155415387552508321802243055, 1.0000000000000000000000000000000000000]
[3.3977035170695895892746281275100215092, -1.2095696424892583832474261333152633094, -0.34126823285394525048749673328351439472, 1.5306621354683455615906467453926368481]
取其中第一组,可以得到这四组点都可以和虚点$(3.3977035170695895892746281275100215092+1.2095696424892583832474261333152633094i,-0.34126823285394525048749673328351439472+1.8514424519702915249627830451131201330i)$及其共轭点确定圆锥曲线如图:
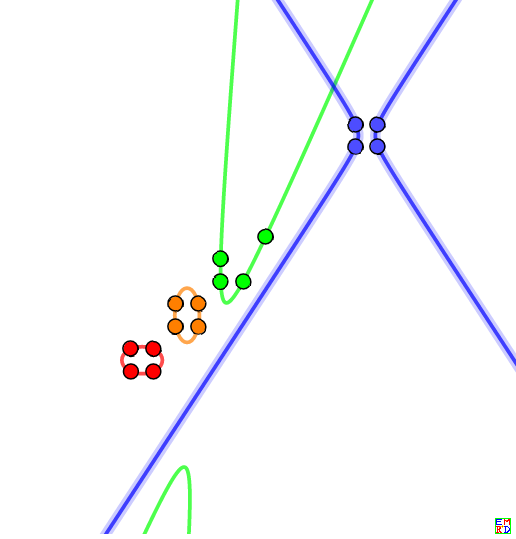
对应坐标方程:
x^2-x+2.2502984396849894757510607258767604052*y^2 - 2.2502984396849894757510607258767604052*y=0
x^2 - 5*x + (0.20641504661085802714202773907993901822*y^2 - 1.0320752330542901357101386953996950911*y + 7.2384902796651481628521664344796341093)=0
x^2 + (-0.51751553864970893444954132470608444132*y - 6.9299378454011642622018347011756622348)*x + (0.035031077299417868899082649412168882630*y^2 + 1.7547824589040749177064214541148178216*y + 12.420372927593014426788991792946026592)=0
x^2 - 21*x + (-0.42799566376720509964304800932967663725*y^2 + 8.9879089391113070925040081959232093824*y + 62.920476985607439039264718973735569900)=0
我们需要将虚点$(3.3977035170695895892746281275100215092+1.2095696424892583832474261333152633094i,-0.34126823285394525048749673328351439472+1.8514424519702915249627830451131201330i)$ 映射为虚圆点$(1,i,0)$,同时其共轭点映射为$(1,-i,0)$, 我们在加上约束条件变换保持(0,0,1), (1,0,1)不变,利用链接中计算方法,可以得到变换矩阵
[-1, 0.30469185648741416715476766528927951236, 0]
[0, -1.8913281181230178415750065410370865488, 0]
[0.38158353291439615467212523887276807783, -0.24929311575192315734302049841351603663, -1.3815835329143961546721252388727680778]
由此将上面圆锥曲线变换为
x^2+y^2-x-0.67544871555867683577169513262020712107*2*y=0
x^2+y^2-2*2.1171510815205749140321101529459489720*x-2*4.4141437221310586865025261856136175234*y+22.150077989349251499282581513542942265=0
x^2+y^2-2*0.74744558515194252015094028992137252984*x-2*15.719255161278792577340072102853639386*y+194.48421204411773560132642833478575214=0
x^2+y^2-2*15617.481802752951690068004138873436925*x+2*5718.9228242383352897882804282297807531*y-103407.45413472270552830847021773145316=0
对应四组点坐标转化为
[0,0,1], [1,0,1], [-0.18682703976207016151639617952867705935, 1.1597002873697944713909462289358480507,1], [0.55656125431708197418853161517470635357, 1.5139186266824718455600491742707080636,1]
[1.2449533817431600291551788547297097889, 3.3864342861684846631331853869688947378,1], [0.79479452336698431506486674960951712303, 4.1528227597653978048625702833421924553,1], [3.2506853215210722979892680650441648033, 5.1435377439121673250049551342497790372,1], [2.1183085352758874858112799905239497390, 5.7620733095221545346435780034807917957,1]
[3.2627419481433368016194208581612562022, 8.8750802738027560330303013465936425565,1], [2.2478960189195233153044605376262428670, 8.5835635914418484523586811048637697357,1], [8.0308511909126574421457439996425687647, 16.067749732267705857988307744672607565,1], [7.0968997545211578725818759582981666453, 19.304485619020001843027993629945178424,1]
[118.49279341679442177689298347680667582, 322.31573019116911740433449558200361221,1], [-103.90272884896751209881481571123720378, -282.62886671944580879769087532683801230,1], [21.587609524407694901071931649621869162, 67.553469385329820031517242610746277143,1], [-24.629850382882953087005377745528997702, -58.572427497810882565065603263668676778,1]
上面求共轭虚点的pari/gp代码如下:
- conx(X)=
- {
- local(m);
- m=matrix(6,6);
- for(u=1,6,
- m[u,1]=X[u][1]*X[u][1];
- m[u,2]=X[u][2]*X[u][1];
- m[u,3]=X[u][2]*X[u][2];
- m[u,4]=X[u][1]*X[u][3];
- m[u,5]=X[u][2]*X[u][3];
- m[u,6]=X[u][3]*X[u][3];
- );
- matdet(m)
- }
- P1=conx([[0,0,1],[1,0,1],[0,1,1],[1,1,1],[a+b*I,c+b*r*I,1],[a-b*I,c-b*r*I,1]])/(b*I);
- P2=conx([[2,2,1],[2,3,1],[3,2,1],[3,3,1],[a+b*I,c+b*r*I,1],[a-b*I,c-b*r*I,1]])/(b*I);
- P3=conx([[4,4,1],[4,5,1],[5,4,1],[6,6,1],[a+b*I,c+b*r*I,1],[a-b*I,c-b*r*I,1]])/(b*I);
- P4=conx([[10,10,1],[11,11,1],[10,11,1],[11,10,1],[a+b*I,c+b*r*I,1],[a-b*I,c-b*r*I,1]])/(b*I);
- H11=deriv(P1,a);H12=deriv(P1,b);H13=deriv(P1,c);H14=deriv(P1,r);
- H21=deriv(P2,a);H22=deriv(P2,b);H23=deriv(P2,c);H24=deriv(P2,r);
- H31=deriv(P3,a);H32=deriv(P3,b);H33=deriv(P3,c);H34=deriv(P3,r);
- H41=deriv(P4,a);H42=deriv(P4,b);H43=deriv(P4,c);H44=deriv(P4,r);
- vapply(f,x)={
- subst(subst(subst(subst(f,a,x[1]),b,x[2]),c,x[3]),r,x[4])
- }
- iterf(x)={
- local(m);
- m=matrix(4,4);
- m[1,1]=vapply(H11,x); m[1,2]=vapply(H12,x); m[1,3]=vapply(H13,x); m[1,4]=vapply(H14,x);
- m[2,1]=vapply(H21,x); m[2,2]=vapply(H22,x); m[2,3]=vapply(H23,x); m[2,4]=vapply(H24,x);
- m[3,1]=vapply(H31,x); m[3,2]=vapply(H32,x); m[3,3]=vapply(H33,x); m[3,4]=vapply(H34,x);
- m[4,1]=vapply(H41,x); m[4,2]=vapply(H42,x); m[4,3]=vapply(H43,x); m[4,4]=vapply(H44,x);
- x-m^-1*[vapply(P1,x),vapply(P2,x),vapply(P3,x),vapply(P4,x)]~
- }
- genone()={
- local(x);
- x=vector(4)~;
- for(u=1,4, x[u]=random(200)-100.0);
- for(u=1,1000, x=iterf(x));
- x
- }
===================
\(\begin{cases}143451r^6 - 1445256r^5 + 2819816r^4 - 2709866r^3 + 2819816r^2 - 1445256r + 143451=0\\
2521355742675r^5-26245123391808r^4+44846306763281r^3+53963393585191r^2\\-67977224798104r-53603603209827=-19706658745104c\\
-854055968689539r^5+8478577046022003r^4-15649755072930989r^3+14973546480184634r^2\\-16845680109446093r+7405983892652979=-37771095928116b^2\\
-\frac{5590675035099}{2189628749456}r^6+\frac{58700662713981}{2189628749456}r^5-\frac{396230081423371}{6568886248368}r^4\\+\frac{10315296251}{164123682}r^3-\frac{444649007775197}{6568886248368}r^2+\frac{337310120365633}{6568886248368}r\frac{-22873470451245}{2189628749456}=c-a\end{cases}\)
|
|