三角形的角格点问题

mathe · 发表于 2019-10-12 11:11:42

而对于一般情况计算第二类解的数目的难点在于有些时候U,V,W三者或X,Y,Z三者之间有相等的值，减少了总数。
可以看出这些情况只会出现在$t=1/8,1/9,1/12,1/15,1/18,1/24,1/30$等情况，也就是除了n是8,9,12,15,18,24,30的倍数以及表格四第一列中数的倍数时，其它情况情况的解可以统一计数，所以最终公式会有点复杂，需要判断n是否这些数的倍数做出对应的调整。

设$\delta_h(k)$在k为h的倍数时等于1，不然等于0.
第二类解存在一个前提是n是6的倍数，所以我们可以记$n=6k$

对于其中第一条，要求$1\le nt \le k-1$, 其中$nt = {2k}/3$即$t=1/9$时,对应6组解；$nt = k/2$即$t=1/12$时,对应4组解；其余情况都对应12组解。
所以
i) k是6的倍数，这部分有$12(k-1)-14$组解
ii) k是3的倍数但是不是2的倍数，这部分有$12(k-1)-6$组解
iii)k是2的倍数但是不是3的倍数，这部分有$12(k-1)-8$组解
iv)k不是2的倍数也不是3的倍数，这部分有$12(k-1)$组解
可以写成：基础解12(k-1), 如果k是3的倍数减去6，2的倍数再减去8，即$12(k-1)-6\delta_3(k)-8\delta_2(k)$

对于其中第二条，要求$1\le nt \le k-1$且$nt \ne k/2$，其中$nt=k/3, {2k}/3, {3k}/4$,即$t=1/18,1/9,1/8$时分别会出现重复数字
所以
i) k是12的倍数，这部分有$12(k-2)-18$组解
ii) k是6的倍数但是不是12的倍数，这部分有$12(k-2)-12$组解
ii) k是4的倍数但是不是3的倍数，这部分有$12(k-2)-6$组解
iii) k是3的倍数但是不是2的倍数，这部分有$12(k-1)-12$组解
iv) k是2的倍数但是不是3和4的倍数，这部分有$12(k-2)$组解
iv)k既不是2的倍数也不是3的倍数，这部分有$12(k-1)$组解
基础解为12(k-1), 如果k是3的倍数，减去12，如果k是2的倍数，减去12，如果k还是4的倍数，再减去6,即$12(k-1)-12\delta_3(k)-12\delta_2(k)-6\delta_4(k)$

其中第三条也比较简单，要求$1\le nt \le k/2$，其中$nt=k/3,k/4$即$t=1/18,1/24$时分别会出现重复数字
所以
i)k是12的倍数，这部分有$12\floor({k-1}/2)-12$组解
ii)k是4的倍数但是不是3的倍数，这部分有$12\floor({k-1}/2)-6$组解
ii)k是3的倍数但是不是4的倍数，这部分有$12\floor({k-1}/2)-6$组解
iv)k既不是3的倍数也不是4的倍数，这部分有$12\floor({k-1}/2)$组解
基础解$12\floor({k-1}/2)$，如果k是3的倍数减去6，如果k是4的倍数减去6.即$12\floor({k-1}/2)-6\delta_3(k)-6\delta_4(k)$

其中第四条比较复杂，要求$1\le nt \le k/2$，但是其中$t=1/18,1/24$分别和第一条和第二条重叠，需要删除，而$t=1/15,1/30$有重复数字
也就是$tn=k/3,k/4$时需要去除，$tn={2k}/5,k/5$时有重复数字。
所以同样可以得出解的数目为$12\floor({k-1}/2)-12\delta_3(k)-12\delta_4(k)-12\delta_5(k)$
所以汇总后第二类解的总数为$24(k-1)+24\floor({k-1}/2)-20\delta_2(k)-36\delta_3(k)-24\delta_4(k)-12\delta_5(k)$

mathe · 发表于 2019-10-12 12:57:31

而第3组应该为$(8*6+5*12)\delta_5(k)+6*12\delta_7(k)+22*12\delta_10(k)+8*12\delta_14(k)+4*12\delta_15(k)+8*12\delta_20(k)+4*12\delta_35(k)$

mathe · 发表于 2019-10-12 13:02:37

最终解的总数可以写成
${\delta_2(n)(n-2)(n-6)}/8+{delta_4(n)}/2+\delta_6(n)(6n-35)-32\delta_12(n)-36\delta_18(n)-24\delta_24(n)+96\delta_30(n)+72\delta_42(n)+264\delta_60(n)+96\delta_84(n)+48\delta_90(n)+96\delta_120(n)+48\delta_210(n)$
对于15°角倍数情况对应n=12,结果为13
对于10°角倍数情况对应n=18,结果为61
对于3°角倍数情况对应n=60,结果为1045
对于整数角度情况对应n=180,结果是5257

mathe · 发表于 2019-10-12 18:57:50

wayne问的其实和大家讨论的是不同的问题。wanye的问题是给定一个三个角都是有理度数的三角形，其内部有多少个满足条件的P点。当然在三角形为等腰三角形时，其对称轴上可以有无穷多个点，使得它分割的三个小三角形的角都是有理度数。但是对于非等腰三角形(或者等腰三角形去除对称轴上的点)，总是有而且只有有限个点满足条件。其中，每个三角形通常至少有三个第一类点，分别为角平分线交点和前面提到第一类一对共轭点(但是对于正三角形三个点重合)。而只有极少数三角形会拥有第二类和第三类点。所以对于给定的三角形，计算满足条件的所有P点也不能难，按上面公式逐一匹配即可。但是我们还有一个问题，非等腰三角形最多可以拥有几个满足条件的P点？等腰三角形最多可以拥有多少个不在对称轴上的满足条件的P点。

这问题有点困难，其中第一类点比较简单，几乎每个三角形都三个解（去除等腰三角形对称轴上点）。第三类只有几个固定三角形，主要复杂的情况在于第二类。一种比较可行的方案是将第二类所有对应的三角形在平面坐标上画出来。每个三角形有三个角，我们选择其中两个较小的角分别作为横纵坐标，那么第二类四种情况每种根据(U,V,W)和(X,Y,Z)之间不同组合有6个三角形包含一个参数t,对应6条坐标平面上折线（$A<=B<=C$)。
而所有第三类情况的需要转化为图上的孤立点。我们最后需要在图上找出经过的折线或孤立点最多的点。

王守恩 · 发表于 2019-10-13 06:31:17

本帖最后由王守恩于 2019-10-13 15:08 编辑

mathe 发表于 2019-10-12 18:57
wayne问的其实和大家讨论的是不同的问题。wanye的问题是给定一个三个角都是有理度数的三角形，其内部有多少 ...

谢谢 mathe！6 楼的 65 个解。
01：$(\sin012\pi/2520)(\sin540\pi/2520)(\sin1452\pi/2520)=(\sin132\pi/2520)(\sin168\pi/2520)(\sin0216\pi/2520)$
02：$(\sin021\pi/2520)(\sin546\pi/2520)(\sin1281\pi/2520)=(\sin126\pi/2520)(\sin210\pi/2520)(\sin0336\pi/2520)$
03：$(\sin021\pi/2520)(\sin672\pi/2520)(\sin1113\pi/2520)=(\sin126\pi/2520)(\sin231\pi/2520)(\sin0357\pi/2520)$
04：$(\sin021\pi/2520)(\sin756\pi/2520)(\sin1029\pi/2520)=(\sin147\pi/2520)(\sin210\pi/2520)(\sin0357\pi/2520)$
05：$(\sin021\pi/2520)(\sin882\pi/2520)(\sin0903\pi/2520)=(\sin147\pi/2520)(\sin231\pi/2520)(\sin0336\pi/2520)$
06：$(\sin028\pi/2520)(\sin476\pi/2520)(\sin1316\pi/2520)=(\sin140\pi/2520)(\sin224\pi/2520)(\sin0336\pi/2520)$
07：$(\sin028\pi/2520)(\sin644\pi/2520)(\sin0868\pi/2520)=(\sin112\pi/2520)(\sin168\pi/2520)(\sin0700\pi/2520)$
08：$(\sin030\pi/2520)(\sin420\pi/2520)(\sin1290\pi/2520)=(\sin120\pi/2520)(\sin180\pi/2520)(\sin0480\pi/2520)$
09：$(\sin030\pi/2520)(\sin540\pi/2520)(\sin1110\pi/2520)=(\sin120\pi/2520)(\sin210\pi/2520)(\sin0510\pi/2520)$
10：$(\sin030\pi/2520)(\sin600\pi/2520)(\sin1050\pi/2520)=(\sin150\pi/2520)(\sin180\pi/2520)(\sin0510\pi/2520)$
11：$(\sin030\pi/2520)(\sin750\pi/2520)(\sin0900\pi/2520)=(\sin150\pi/2520)(\sin210\pi/2520)(\sin0480\pi/2520)$
12：$(\sin042\pi/2520)(\sin252\pi/2520)(\sin1302\pi/2520)=(\sin084\pi/2520)(\sin168\pi/2520)(\sin0672\pi/2520)$
13：$(\sin042\pi/2520)(\sin273\pi/2520)(\sin1533\pi/2520)=(\sin126\pi/2520)(\sin210\pi/2520)(\sin0336\pi/2520)$
14：$(\sin042\pi/2520)(\sin336\pi/2520)(\sin1134\pi/2520)=(\sin084\pi/2520)(\sin210\pi/2520)(\sin0714\pi/2520)$
15：$(\sin042\pi/2520)(\sin420\pi/2520)(\sin1050\pi/2520)=(\sin126\pi/2520)(\sin168\pi/2520)(\sin0714\pi/2520)$
16：$(\sin042\pi/2520)(\sin420\pi/2520)(\sin1302\pi/2520)=(\sin168\pi/2520)(\sin252\pi/2520)(\sin0336\pi/2520)$
17：$(\sin042\pi/2520)(\sin546\pi/2520)(\sin0924\pi/2520)=(\sin126\pi/2520)(\sin210\pi/2520)(\sin0672\pi/2520)$
18：$(\sin042\pi/2520)(\sin546\pi/2520)(\sin1050\pi/2520)=(\sin126\pi/2520)(\sin336\pi/2520)(\sin0420\pi/2520)$
19：$(\sin042\pi/2520)(\sin546\pi/2520)(\sin1134\pi/2520)=(\sin210\pi/2520)(\sin252\pi/2520)(\sin0336\pi/2520)$
20：$(\sin042\pi/2520)(\sin588\pi/2520)(\sin1050\pi/2520)=(\sin168\pi/2520)(\sin294\pi/2520)(\sin0378\pi/2520)$
21：$(\sin042\pi/2520)(\sin672\pi/2520)(\sin0756\pi/2520)=(\sin126\pi/2520)(\sin210\pi/2520)(\sin0714\pi/2520)$
22：$(\sin042\pi/2520)(\sin672\pi/2520)(\sin0966\pi/2520)=(\sin210\pi/2520)(\sin252\pi/2520)(\sin0378\pi/2520)$
23：$(\sin042\pi/2520)(\sin756\pi/2520)(\sin0882\pi/2520)=(\sin210\pi/2520)(\sin294\pi/2520)(\sin0336\pi/2520)$
24：$(\sin056\pi/2520)(\sin532\pi/2520)(\sin0896\pi/2520)=(\sin140\pi/2520)(\sin252\pi/2520)(\sin0644\pi/2520)$
25：$(\sin060\pi/2520)(\sin120\pi/2520)(\sin1560\pi/2520)=(\sin060\pi/2520)(\sin180\pi/2520)(\sin0540\pi/2520)$
26：$(\sin060\pi/2520)(\sin210\pi/2520)(\sin1470\pi/2520)=(\sin120\pi/2520)(\sin180\pi/2520)(\sin0480\pi/2520)$
27：$(\sin060\pi/2520)(\sin420\pi/2520)(\sin0780\pi/2520)=(\sin120\pi/2520)(\sin180\pi/2520)(\sin0960\pi/2520)$
28：$(\sin060\pi/2520)(\sin420\pi/2520)(\sin1140\pi/2520)=(\sin180\pi/2520)(\sin240\pi/2520)(\sin0480\pi/2520)$
29：$(\sin060\pi/2520)(\sin540\pi/2520)(\sin0900\pi/2520)=(\sin120\pi/2520)(\sin420\pi/2520)(\sin0480\pi/2520)$
30：$(\sin072\pi/2520)(\sin336\pi/2520)(\sin1164\pi/2520)=(\sin180\pi/2520)(\sin204\pi/2520)(\sin0564\pi/2520)$
31：$(\sin084\pi/2520)(\sin084\pi/2520)(\sin1764\pi/2520)=(\sin084\pi/2520)(\sin168\pi/2520)(\sin0336\pi/2520)$
32：$(\sin084\pi/2520)(\sin126\pi/2520)(\sin1386\pi/2520)=(\sin084\pi/2520)(\sin168\pi/2520)(\sin0672\pi/2520)$
33：$(\sin084\pi/2520)(\sin168\pi/2520)(\sin1344\pi/2520)=(\sin084\pi/2520)(\sin252\pi/2520)(\sin0588\pi/2520)$
34：$(\sin084\pi/2520)(\sin168\pi/2520)(\sin1596\pi/2520)=(\sin168\pi/2520)(\sin252\pi/2520)(\sin0252\pi/2520)$
35：$(\sin084\pi/2520)(\sin210\pi/2520)(\sin1470\pi/2520)=(\sin168\pi/2520)(\sin252\pi/2520)(\sin0336\pi/2520)$
36：$(\sin084\pi/2520)(\sin252\pi/2520)(\sin1092\pi/2520)=(\sin084\pi/2520)(\sin336\pi/2520)(\sin0672\pi/2520)$
37：$(\sin084\pi/2520)(\sin252\pi/2520)(\sin1176\pi/2520)=(\sin168\pi/2520)(\sin168\pi/2520)(\sin0672\pi/2520)$
38：$(\sin084\pi/2520)(\sin294\pi/2520)(\sin0798\pi/2520)=(\sin126\pi/2520)(\sin168\pi/2520)(\sin1050\pi/2520)$
39：$(\sin084\pi/2520)(\sin420\pi/2520)(\sin0924\pi/2520)=(\sin168\pi/2520)(\sin252\pi/2520)(\sin0672\pi/2520)$
40：$(\sin084\pi/2520)(\sin420\pi/2520)(\sin1092\pi/2520)=(\sin252\pi/2520)(\sin336\pi/2520)(\sin0336\pi/2520)$
41：$(\sin084\pi/2520)(\sin588\pi/2520)(\sin0672\pi/2520)=(\sin168\pi/2520)(\sin252\pi/2520)(\sin0756\pi/2520)$
42：$(\sin084\pi/2520)(\sin588\pi/2520)(\sin0756\pi/2520)=(\sin168\pi/2520)(\sin336\pi/2520)(\sin0588\pi/2520)$
43：$(\sin120\pi/2520)(\sin390\pi/2520)(\sin0690\pi/2520)=(\sin180\pi/2520)(\sin210\pi/2520)(\sin0930\pi/2520)$
44：$(\sin120\pi/2520)(\sin480\pi/2520)(\sin0780\pi/2520)=(\sin180\pi/2520)(\sin420\pi/2520)(\sin0540\pi/2520)$
45：$(\sin126\pi/2520)(\sin210\pi/2520)(\sin1050\pi/2520)=(\sin126\pi/2520)(\sin252\pi/2520)(\sin0756\pi/2520)$
46：$(\sin126\pi/2520)(\sin210\pi/2520)(\sin1134\pi/2520)=(\sin168\pi/2520)(\sin210\pi/2520)(\sin0672\pi/2520)$
47：$(\sin126\pi/2520)(\sin210\pi/2520)(\sin1218\pi/2520)=(\sin168\pi/2520)(\sin252\pi/2520)(\sin0546\pi/2520)$
48：$(\sin126\pi/2520)(\sin252\pi/2520)(\sin0966\pi/2520)=(\sin168\pi/2520)(\sin210\pi/2520)(\sin0798\pi/2520)$
49：$(\sin126\pi/2520)(\sin462\pi/2520)(\sin0756\pi/2520)=(\sin210\pi/2520)(\sin294\pi/2520)(\sin0672\pi/2520)$
50：$(\sin126\pi/2520)(\sin483\pi/2520)(\sin0609\pi/2520)=(\sin168\pi/2520)(\sin273\pi/2520)(\sin0861\pi/2520)$
51：$(\sin140\pi/2520)(\sin364\pi/2520)(\sin0980\pi/2520)=(\sin308\pi/2520)(\sin336\pi/2520)(\sin0392\pi/2520)$
52：$(\sin156\pi/2520)(\sin252\pi/2520)(\sin0996\pi/2520)=(\sin180\pi/2520)(\sin288\pi/2520)(\sin0648\pi/2520)$
53：$(\sin168\pi/2520)(\sin168\pi/2520)(\sin1176\pi/2520)=(\sin168\pi/2520)(\sin252\pi/2520)(\sin0588\pi/2520)$
54：$(\sin168\pi/2520)(\sin336\pi/2520)(\sin0924\pi/2520)=(\sin252\pi/2520)(\sin420\pi/2520)(\sin0420\pi/2520)$
55：$(\sin168\pi/2520)(\sin420\pi/2520)(\sin0672\pi/2520)=(\sin252\pi/2520)(\sin252\pi/2520)(\sin0756\pi/2520)$
56：$(\sin168\pi/2520)(\sin462\pi/2520)(\sin0546\pi/2520)=(\sin210\pi/2520)(\sin252\pi/2520)(\sin0882\pi/2520)$
57：$(\sin168\pi/2520)(\sin492\pi/2520)(\sin0576\pi/2520)=(\sin180\pi/2520)(\sin372\pi/2520)(\sin0732\pi/2520)$
58：$(\sin180\pi/2520)(\sin300\pi/2520)(\sin0900\pi/2520)=(\sin240\pi/2520)(\sin300\pi/2520)(\sin0600\pi/2520)$
59：$(\sin180\pi/2520)(\sin330\pi/2520)(\sin0690\pi/2520)=(\sin210\pi/2520)(\sin240\pi/2520)(\sin0870\pi/2520)$
60：$(\sin210\pi/2520)(\sin336\pi/2520)(\sin0798\pi/2520)=(\sin252\pi/2520)(\sin378\pi/2520)(\sin0546\pi/2520)$
61：$(\sin210\pi/2520)(\sin399\pi/2520)(\sin0609\pi/2520)=(\sin252\pi/2520)(\sin273\pi/2520)(\sin0777\pi/2520)$
62：$(\sin210\pi/2520)(\sin420\pi/2520)(\sin0714\pi/2520)=(\sin336\pi/2520)(\sin378\pi/2520)(\sin0462\pi/2520)$
63：$(\sin210\pi/2520)(\sin540\pi/2520)(\sin0570\pi/2520)=(\sin330\pi/2520)(\sin390\pi/2520)(\sin0480\pi/2520)$
64：$(\sin252\pi/2520)(\sin336\pi/2520)(\sin0756\pi/2520)=(\sin336\pi/2520)(\sin420\pi/2520)(\sin0420\pi/2520)$
65：$(\sin273\pi/2520)(\sin378\pi/2520)(\sin0651\pi/2520)=(\sin336\pi/2520)(\sin399\pi/2520)(\sin0483\pi/2520)$

mathe · 发表于 2019-10-13 06:41:02

原来第一类解都很特殊，我们已经知道第一类解可以产生三角形的内心，等腰三角形对称轴上的点。
而余下两个点是三角形的外心和外心的等角共轭也就是垂心。
所以这两个解在三角形是直角三角形或钝角三角形时会跑到三角形的边界上和外面（增根）。
从另外一个角度，我们还可以继续分析在三角形外部的P点情况。同样，除掉对称轴上的点，三边和延长线上的点，即使包含三角形的外部，对于给定的三角形，也应该只有有限个合法的P点构成角格点。比如这时三角形的三个旁心也都包含进来了。对于这种推广情况，我们应该统一称为角格点四点形更加合理（其实四个点的地位是等价的）。

发现等腰三角形以它顶点作为圆心，在圆周上可以找出无限个符合条件的圆。也就是把这个顶点看出另外三点的外心。所以我们还要排除这个角格点圆。
同样对于6个角度u,v,w;x,y,z。点P在三角形外部意味着这6个角度正好有两个是负角度。这个问题其第二类和第三类解的答案还没有。但是其第一类解还是比较简单的。由于A=u+x>0,B=v+y>0,C=w+z>0,这意味着这三组角中每组最多一个负角度，而正弦值乘积相等意味这负角度数目为偶数。
设${|u|,|v|,|w|}={|x|,|y|,|z|}={a,b,c}$且$a\le b \le c$,这时的第一类解分别只能是
i)$u=-a,v=b,w=c;x=b,y=-a,z=c$
ii) $u=-a,v=b,w=c;x=c,y=b,z=-a$
iii)$u=-a,v=b,w=c;x=b,y=c,z=-a$
iv)$u=-a,v=-b,w=c;x=b,y=c,w=a$
v)$u=-a,v=b,w=c;x=c,y=a,z=-b$
其中i),ii)属于等腰三角形对称轴形式
其中iv)如果是等腰三角形，意味着 $A=B=b-a=c-b, C=a+c, c=pi/2$
于是$/_APB=b+B-a=2(b-a)$, 所以$/_APB+C=2(b-a)+a+c=b-a+c-b+a+c=2c=pi$, 于是APBC四点共圆，P在三角形ABC外接圆上

wayne · 发表于 2019-10-13 10:06:20

太赞了，竟无语凝噎。
得空好好研读一下

mathe · 发表于 2019-10-13 13:33:26

穷举得出一个三角形内部最多14个非平凡角格点（也就是不在对称轴上），里面每个有理数代表对应角为$pi$的这个倍数。
第一行数据为三角形三个顶点，后面各行分别是U,V,W;X,Y,Z, 其中U+X,V+Y,W+Z等于三个角

tran.out (6.22 KB, 下载次数: 0)
Triangle: {7/30,3/10,7/15} has 14 rational angle points
      {1/30,1/6,2/5:1/5,2/15,1/15}
      {1/30,1/5,11/30:1/5,1/10,1/10}
      {1/30,4/15,1/5:7/60,3/20,7/30}
      {1/15,2/15,11/30:1/6,1/6,1/10}
      {1/12,1/6,17/60:3/20,2/15,11/60}
      {1/10,1/30,13/30:2/15,4/15,1/30}
      {1/10,2/15,3/10:2/15,1/6,1/6}
      {7/60,3/20,7/30:7/60,3/20,7/30}
      {2/15,1/12,19/60:1/10,13/60,3/20}
      {1/6,1/60,5/12:1/15,17/60,1/20}
      {1/6,1/30,11/30:1/15,4/15,1/10}
      {1/6,1/10,1/5:1/15,1/5,4/15}
      {1/6,1/5,1/15:1/15,1/10,2/5}
      {1/5,1/30,4/15:7/60,3/20,7/30}

其次为12个
Triangle: {1/6,3/10,8/15} has 12 rational angle points
      {1/60,7/30,5/12:3/20,1/15,7/60}
      {1/30,1/6,13/30:2/15,2/15,1/10}
      {1/30,7/30,3/10:2/15,1/15,7/30}
      {1/30,4/15,1/6:2/15,1/30,11/30}
      {1/15,1/15,7/15:1/10,7/30,1/15}
      {1/15,2/15,11/30:1/10,1/6,1/6}
      {1/15,1/6,3/10:1/10,2/15,7/30}
      {1/15,13/60,11/60:1/10,1/12,7/20}
      {1/12,3/20,4/15:1/12,3/20,4/15}
      {1/10,1/30,7/15:1/15,4/15,1/15}
      {2/15,1/60,9/20:1/30,17/60,1/12}
      {2/15,1/6,1/15:1/30,2/15,7/15}
Triangle: {1/6,11/30,7/15} has 12 rational angle points
      {1/60,4/15,23/60:3/20,1/10,1/12}
      {1/30,1/10,13/30:2/15,4/15,1/30}
      {1/30,1/6,2/5:2/15,1/5,1/15}
      {1/30,3/10,7/30:2/15,1/15,7/30}
      {1/30,1/3,2/15:1/12,11/60,7/30}
      {1/15,4/15,1/6:1/10,1/10,3/10}
      {1/12,11/60,7/30:1/12,11/60,7/30}
      {1/10,1/20,23/60:1/15,19/60,1/12}
      {1/10,1/6,1/5:1/15,1/5,4/15}
      {2/15,1/30,1/3:1/12,11/60,7/30}
      {2/15,1/10,1/6:1/30,4/15,3/10}
      {3/20,1/20,1/6:1/60,19/60,3/10}
等腰三角形非对称轴结果最多是8个
Triangle: {7/30,7/30,8/15} has 8 rational angle points
      {1/30,1/6,2/5:1/5,1/15,2/15}
      {1/15,2/15,11/30:1/6,1/10,1/6}
      {1/12,2/15,19/60:3/20,1/10,13/60}
      {2/15,1/15,11/30:1/10,1/6,1/6}
      {2/15,1/12,19/60:1/10,3/20,13/60}
      {2/15,1/6,1/10:1/10,1/15,13/30}
      {1/6,1/30,2/5:1/15,1/5,2/15}
      {1/6,2/15,1/10:1/15,1/10,13/30}

mathe · 发表于 2019-10-13 15:09:34

上面程序忘了模式中(U,V,W)和(X,Y,Z)可以交换（前面的结果除了第一类点每个结果应该继续加上每个点的等角共轭结果），导致结果过少，最多应该是25个
Triangle: {7/30,3/10,7/15} has 25 rational angle points
      {1/30,1/6,2/5:1/5,2/15,1/15}
      {1/30,1/5,11/30:1/5,1/10,1/10}
      {1/30,4/15,1/5:7/60,3/20,7/30}
      {1/15,1/10,2/5:1/6,1/5,1/15}
      {1/15,2/15,11/30:1/6,1/6,1/10}
      {1/15,1/5,4/15:1/6,1/10,1/5}
      {1/15,4/15,1/10:1/6,1/30,11/30}
      {1/15,17/60,1/20:1/6,1/60,5/12}
      {1/12,1/6,17/60:3/20,2/15,11/60}
      {1/10,1/30,13/30:2/15,4/15,1/30}
      {1/10,2/15,3/10:2/15,1/6,1/6}
      {1/10,13/60,3/20:2/15,1/12,19/60}
      {7/60,3/20,7/30:7/60,3/20,7/30}
      {2/15,1/12,19/60:1/10,13/60,3/20}
      {2/15,1/6,1/6:1/10,2/15,3/10}
      {2/15,4/15,1/30:1/10,1/30,13/30}
      {3/20,2/15,11/60:1/12,1/6,17/60}
      {1/6,1/60,5/12:1/15,17/60,1/20}
      {1/6,1/30,11/30:1/15,4/15,1/10}
      {1/6,1/10,1/5:1/15,1/5,4/15}
      {1/6,1/6,1/10:1/15,2/15,11/30}
      {1/6,1/5,1/15:1/15,1/10,2/5}
      {1/5,1/30,4/15:7/60,3/20,7/30}
      {1/5,1/10,1/10:1/30,1/5,11/30}
      {1/5,2/15,1/15:1/30,1/6,2/5}

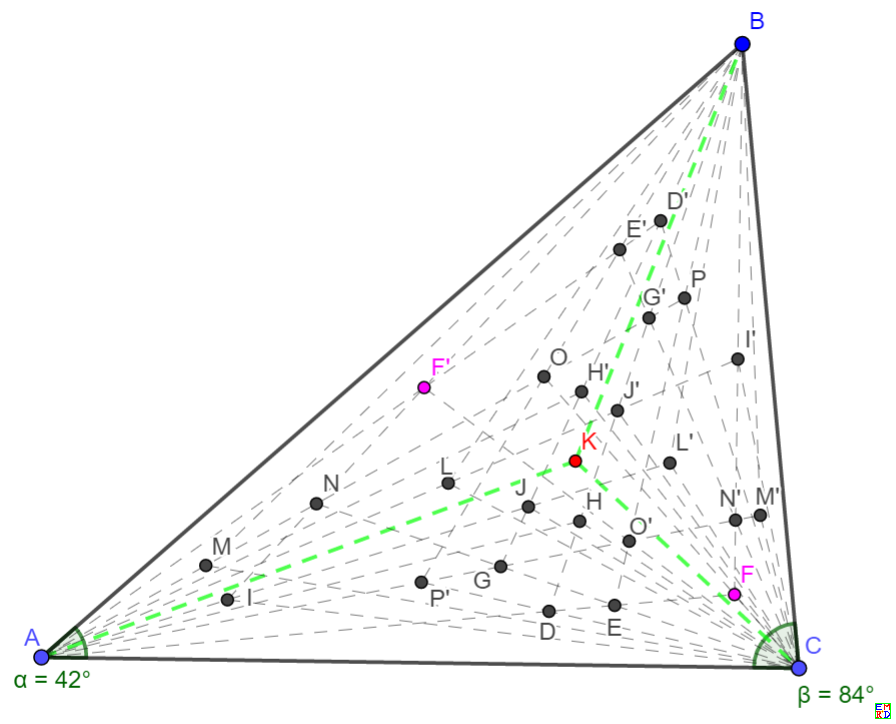
其次23个和21个
Triangle: {1/6,3/10,8/15} has 23 rational angle points
      {1/60,7/30,5/12:3/20,1/15,7/60}
      {1/30,2/15,7/15:2/15,1/6,1/15}
      {1/30,1/6,13/30:2/15,2/15,1/10}
      {1/30,7/30,3/10:2/15,1/15,7/30}
      {1/30,4/15,1/6:2/15,1/30,11/30}
      {1/30,17/60,1/12:2/15,1/60,9/20}
      {1/15,1/15,7/15:1/10,7/30,1/15}
      {1/15,2/15,11/30:1/10,1/6,1/6}
      {1/15,1/6,3/10:1/10,2/15,7/30}
      {1/15,13/60,11/60:1/10,1/12,7/20}
      {1/15,4/15,1/15:1/10,1/30,7/15}
      {1/12,3/20,4/15:1/12,3/20,4/15}
      {1/10,1/30,7/15:1/15,4/15,1/15}
      {1/10,1/12,7/20:1/15,13/60,11/60}
      {1/10,2/15,7/30:1/15,1/6,3/10}
      {1/10,1/6,1/6:1/15,2/15,11/30}
      {1/10,7/30,1/15:1/15,1/15,7/15}
      {2/15,1/60,9/20:1/30,17/60,1/12}
      {2/15,1/30,11/30:1/30,4/15,1/6}
      {2/15,1/15,7/30:1/30,7/30,3/10}
      {2/15,2/15,1/10:1/30,1/6,13/30}
      {2/15,1/6,1/15:1/30,2/15,7/15}
      {3/20,1/15,7/60:1/60,7/30,5/12}
Triangle: {1/6,11/30,7/15} has 21 rational angle points
      {1/60,4/15,23/60:3/20,1/10,1/12}
      {1/60,19/60,3/10:3/20,1/20,1/6}
      {1/30,1/10,13/30:2/15,4/15,1/30}
      {1/30,1/6,2/5:2/15,1/5,1/15}
      {1/30,4/15,3/10:2/15,1/10,1/6}
      {1/30,3/10,7/30:2/15,1/15,7/30}
      {1/30,1/3,2/15:1/12,11/60,7/30}
      {1/15,1/5,4/15:1/10,1/6,1/5}
      {1/15,4/15,1/6:1/10,1/10,3/10}
      {1/15,19/60,1/12:1/10,1/20,23/60}
      {1/12,11/60,7/30:1/12,11/60,7/30}
      {1/10,1/20,23/60:1/15,19/60,1/12}
      {1/10,1/10,3/10:1/15,4/15,1/6}
      {1/10,1/6,1/5:1/15,1/5,4/15}
      {2/15,1/30,1/3:1/12,11/60,7/30}
      {2/15,1/15,7/30:1/30,3/10,7/30}
      {2/15,1/10,1/6:1/30,4/15,3/10}
      {2/15,1/5,1/15:1/30,1/6,2/5}
      {2/15,4/15,1/30:1/30,1/10,13/30}
      {3/20,1/20,1/6:1/60,19/60,3/10}
      {3/20,1/10,1/12:1/60,4/15,23/60}

tran.out (48.43 KB, 下载次数: 4)
而等腰三角形最多16个非平凡点
Triangle: {7/30,7/30,8/15} has 16 rational angle points
      {1/30,1/6,2/5:1/5,1/15,2/15}
      {1/15,1/10,13/30:1/6,2/15,1/10}
      {1/15,2/15,11/30:1/6,1/10,1/6}
      {1/15,1/5,2/15:1/6,1/30,2/5}
      {1/12,2/15,19/60:3/20,1/10,13/60}
      {1/10,1/15,13/30:2/15,1/6,1/10}
      {1/10,3/20,13/60:2/15,1/12,19/60}
      {1/10,1/6,1/6:2/15,1/15,11/30}
      {2/15,1/15,11/30:1/10,1/6,1/6}
      {2/15,1/12,19/60:1/10,3/20,13/60}
      {2/15,1/6,1/10:1/10,1/15,13/30}
      {3/20,1/10,13/60:1/12,2/15,19/60}
      {1/6,1/30,2/5:1/15,1/5,2/15}
      {1/6,1/10,1/6:1/15,2/15,11/30}
      {1/6,2/15,1/10:1/15,1/10,13/30}
      {1/5,1/15,2/15:1/30,1/6,2/5}

wayne · 发表于 2019-10-14 07:51:57

mathe,我觉得很多这样的帖子给的具体结论应该整理成文章,target是全球的用户, 作为静态网页长期存储 , 而不是论坛.

账号		自动登录	找回密码
密码			欢迎注册

[原创] 三角形的角格点问题

点评

点评