圆外切四边形的四内心共圆问题

数学星空

由于对于给定四边形，\(\angle AEB=t\)很容易算出来，然后指定\(\angle APB=t_1\), \(\angle CPD=2t-t_1\),\(t_1\)自已任意取， 这样点P就确定了，多取一些点然后连起来就是轨迹曲线了～现在作图软件应该可以直接做出来吧

wayne

其实吧，轨迹的隐函数表达是很容易给出来的。虽然 这个隐函数本质上是 多项式，非常难以化简，但如果不化简，带着根式 也是无伤大雅的。
已知$a,b,c,d,r$, 那么$A,B,C,D$的坐标是能得到的，设$P={x,y}$，那么$PA,PB,PC,PD$的长度也是可以直接用$x,y$来表达的，进而用$PA,PB,PC,PD$表达四个内心的坐标.现在接下来只有 四个内心点 共圆了。  
已知四个点${x_1,y_1},{x_2,y_2},{x_3,y_3},{x_4,y_4}$，其交点算得出来，然后相交弦定理，得到约束是:
\[x_1^2 x_2 y_3-x_1^2 x_2 y_4-x_1^2 x_3 y_2+x_1^2 x_3 y_4+x_1^2 x_4 y_2-x_1^2 x_4 y_3-x_1 x_2^2 y_3+x_1 x_2^2 y_4+x_1 x_3^2 y_2-x_1 x_3^2 y_4-x_1 x_4^2 y_2+x_1 x_4^2 y_3-x_1 y_2^2 y_3+x_1 y_2^2 y_4+x_1 y_2 y_3^2-x_1 y_2 y_4^2-x_1 y_3^2 y_4+x_1 y_3 y_4^2+x_2^2 x_3 y_1-x_2^2 x_3 y_4-x_2^2 x_4 y_1+x_2^2 x_4 y_3-x_2 x_3^2 y_1+x_2 x_3^2 y_4+x_2 x_4^2 y_1-x_2 x_4^2 y_3+x_2 y_1^2 y_3-x_2 y_1^2 y_4-x_2 y_1 y_3^2+x_2 y_1 y_4^2+x_2 y_3^2 y_4-x_2 y_3 y_4^2+x_3^2 x_4 y_1-x_3^2 x_4 y_2-x_3 x_4^2 y_1+x_3 x_4^2 y_2-x_3 y_1^2 y_2+x_3 y_1^2 y_4+x_3 y_1 y_2^2-x_3 y_1 y_4^2-x_3 y_2^2 y_4+x_3 y_2 y_4^2+x_4 y_1^2 y_2-x_4 y_1^2 y_3-x_4 y_1 y_2^2+x_4 y_1 y_3^2+x_4 y_2^2 y_3-x_4 y_2 y_3^2 =0\]
经过老胡提醒，其实也就是行列式 \[\begin{vmatrix}
x_1^2+y_1^2 & x_1 & y_1 & 1\\
x_2^2+y_2^2& x_2 & y_2 & 1\\
x_3^2+y_3^2& x_3 & y_3 & 1\\
x_4^2+y_4^2& x_4 & y_4 & 1\\
\end{vmatrix}=0
\]

接下来，直接把四个内心 (以下程序中装在表 I4 中）的坐标放进去就行。 就是说，只要给定$a,b,c,d,r$值，我们是很容易画出轨迹图的，利用隐函数作图的功能。

1. cc[{x_,y_}]:={x^2+y^2,x,y,1};
   
2. Block[{a=1,b,c=3/2,d=3/2,r=1,n=5,I4,pA,pB,pC,pD,pE={x,y},pts},b=(-a c d+a r^2+c r^2+d r^2)/(a c+a d+c d-r^2);Print[{a,b,c,d,r}];
   
3. pts={pA,pB,pC,pD}={{(-a d^2+a r^2+2 d r^2)/(d^2+r^2),(2 a d r+d^2 r-r^3)/(d^2+r^2)},{(b c^2-b r^2-2 c r^2)/(c^2+r^2),(2 b c r+c^2 r-r^3)/(c^2+r^2)},{-c,-r},{d,-r}};
   
4. I4=Total/@{{be pA,ae pB,(a+b) pE}/(be+ae+(a+b)),{(c+b) pE,ce pB,be pC}/((c+b)+ce+be),{(c+d) pE,de pC,ce pD}/((c+d)+de+ce),{(a+d) pE,de pA,ae pD}/((a+d)+de+ae)}/.{ae->Norm[pA-pE],be->Norm[pB-pE],ce->Norm[pC-pE],de->Norm[pD-pE]};
   
5. Show[{Graphics[{Thickness[0.005],Point[pts],Circle[],Line[Subsets[pts,{2}]]}],ContourPlot[Det[cc/@I4]==0,{x,-n,n},{y,-n,n},PlotPoints->100,ContourStyle->Red]}]]

复制代码

比如，四边形的边长是$a+b,b+c,c+d,d+a$,内接圆半径是$r$,${a,b,c,d,r}={1/2,1,2,1,1}$

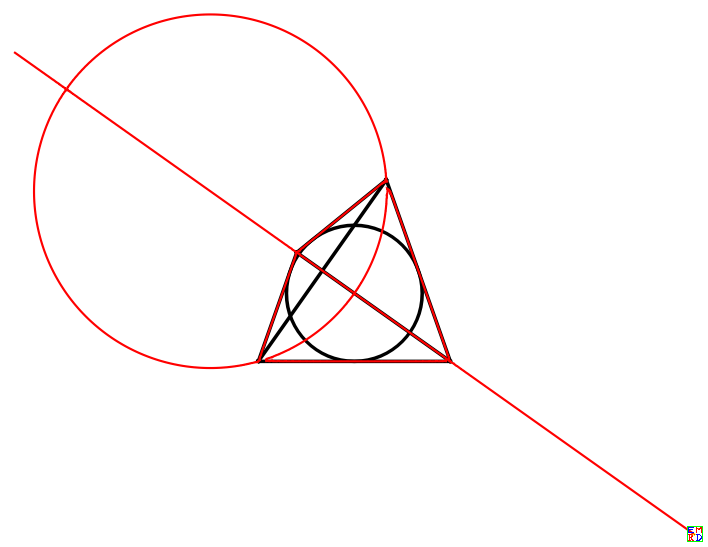
比如，四边形的边长是$a+b,b+c,c+d,d+a$,内接圆半径是$r$,${a,b,c,d,r}={3/2,3/11,2,1,1}$



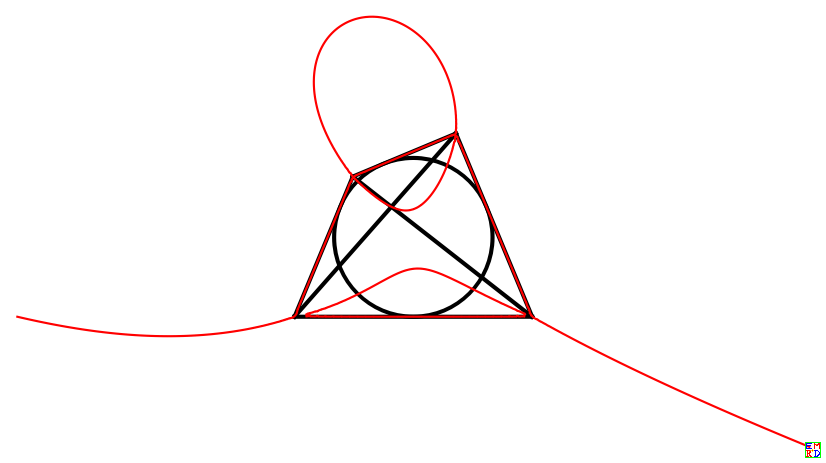
比如，四边形的边长是$a+b,b+c,c+d,d+a$,内接圆半径是$r$,${a,b,c,d,r}={1/2,1/3,2,3,1}$



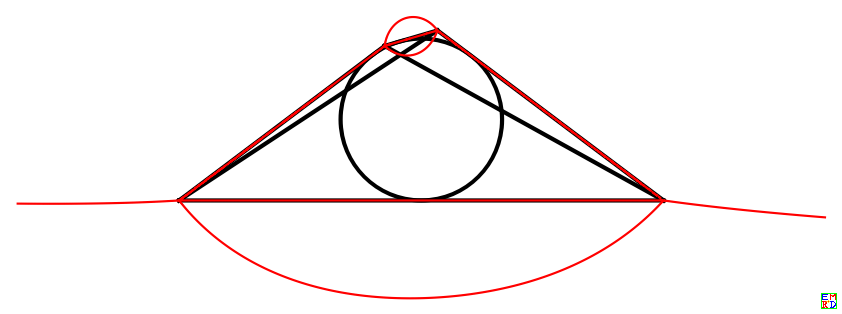
可以看到，轨迹是包含了四边形的边界的

hujunhua

wayne 发表于 2020-9-22 15:45
其实吧，轨迹的隐函数表达是很容易给出来的。虽然 这个隐函数本质上是 多项式，非常难以化简，但如果不化简 ...

记得我们在某个帖子下面讨论过几何方法的意义，当时我顺带举过四点共圆的代数判据。但我找不到那个帖子了，所以只好把判据再写一遍。有此判据，可助上贴。
四点`(x_i,y_i),(i=1,2,3,4)`共圆，即有方程\[
x_i^2+y_i^2+ax_i+by_i+c=0
\]故系数矩阵的行列式\[\begin{vmatrix}
x_1^2+y_1^2 & x_1 & y_1 & 1\\
x_2^2+y_2^2& x_2 & y_2 & 1\\
x_3^2+y_3^2& x_3 & y_3 & 1\\
x_4^2+y_4^2& x_4 & y_4 & 1\\
\end{vmatrix}=0
\]展开行列式即为楼上那个长长的表达式吧。

dlsh

两对对角线分割的三角形的内心四点共圆，这问题相对简单。

数学星空

借用wayne的参数及第二个例子：四边形的边长是$a+b,b+c,c+d,d+a$,内接圆半径是$r$,${a,b,c,d,r}={3/2,3/11,2,1,1}$

利用11#的方法得到：P点的轨迹方程


69754092100*x^10+279016368400*x^9*y+558032736800*x^8*y^2+1116065473600*x^7*y^3+1534590026200*x^6*y^4+1674098210400*x^5*y^5+1953114578800*x^4*y^6+1116065473600*x^3*y^7+1185819565700*x^2*y^8+279016368400*x*y^9+279016368400*y^10+1065335224800*x^9+1426788247500*x^8*y+25365124400*x^7*y^2+754612450900*x^6*y^3-6315915975600*x^5*y^4-6296892132300*x^4*y^5-8446586425200*x^3*y^6-9150468627300*x^2*y^7-3170640550000*x*y^8-3525752291600*y^9+3775995894741*x^8-8368761611700*x^7*y-7948446779861*x^6*y^2-2696197427700*x^5*y^3-9836028387829*x^4*y^4+19713889979700*x^3*y^5+19277267142889*x^2*y^6+14041325795700*x*y^7+17388852856116*y^8-1123546907966*x^7-16249683342242*x^6*y+20086046305052*x^5*y^2+34782051743124*x^4*y^3-8455771685998*x^3*y^4+7340734262974*x^2*y^5-29665364899016*x*y^6-43691000822392*y^7+10403900357802*x^6-11076411751776*x^5*y+10721151474712*x^4*y^2-5749658738152*x^3*y^3-71894929060682*x^2*y^4+29017779203224*x*y^5+61259104415208*y^6+12767327180832*x^5-35756373749544*x^4*y-70926250696*x^3*y^2+77337488945472*x^2*y^3-16030800225328*x*y^4-45918949208384*y^5+15576548098624*x^4-7792417763648*x^3*y-30162627831640*x^2*y^2+7780026298688*x*y^3+15577322565184*y^4+3907017216*x^3-6751468800*x^2*y+25901867520*x*y^2-1949776128*y^3-6910094592*x^2-35755241472*x*y-7465390848*y^2-8631263232*x+24461466624*y-23364829440=0

69754092100*x^10-948655652560*x^9*y+3504445587104*x^8*y^2-3794622610240*x^7*y^3+13320241427416*x^6*y^4-5691933915360*x^5*y^5+19631591680624*x^4*y^6-3794622610240*x^3*y^7+12971470966916*x^2*y^8-948655652560*x*y^9+3225429218704*y^10-162336796160*x^9+1292860390668*x^8*y+929378158016*x^7*y^2-14490841918476*x^6*y^3+3762155251008*x^5*y^4-51229688099436*x^4*y^5+4086828843328*x^3*y^6-53815408880772*x^2*y^7+1416388546496*x*y^8-18369423090480*y^9+695655187605*x^8-2930986242828*x^7*y-9817349145653*x^6*y^2-11259970727628*x^5*y^3+10377946549019*x^4*y^4-13726982726772*x^3*y^5+52990561285417*x^2*y^6-5397998241972*x*y^7+32099610403140*y^8-1500472656550*x^7+1486349532766*x^6*y+28071840656720*x^5*y^2+57029525643916*x^4*y^3+54778653311858*x^3*y^4+71690302366270*x^2*y^5+25206339998588*x*y^6+16147126255120*y^7+2977729828010*x^6+5544616373016*x^5*y-21036491576576*x^4*y^2-18548992747208*x^3*y^3-162858715585454*x^2*y^4-19284381533984*x*y^5-129124578510788*y^6-4605315698340*x^5-17083814363280*x^4*y-70807248204280*x^3*y^2+72957439264080*x^2*y^3-41194225767940*x*y^4+145919700312400*y^5+5428976431160*x^4+41681750076064*x^3*y+14121558845384*x^2*y^2+60641222258736*x*y^3+23161125813520*y^4-6704338255240*x^3-13230190357824*x^2*y-28483990655592*x*y^2-182026878784960*y^3+3254883488820*x^2+17500769400528*x*y+158744846684964*y^2-4365483385400*x-54588173274040*y+6562574425000=0

第一条轨迹：



第二条轨迹：

wayne

数学星空 发表于 2020-9-22 06:39
由于对于给定四边形，\(\angle AEB=t\)很容易算出来，然后指定\(\angle APB=t_1\), \(\angle CPD=2t-t_1\), ...

如果直接使用这个条件，倒是很有可能 大大简化，甚至得到轨迹方程的显式表达。我有空再算算

hujunhua

wayne 发表于 2020-9-23 12:56
如果直接使用这个条件，倒是很有可能 大大简化，甚至得到轨迹方程的显式表达。我有空再算算

直接使用这个条件会漏掉一部分轨迹，还会多出一部分轨迹。
不如你在12楼的方法，能准确地得到所要的轨迹。
不过，有多有少，倒是有助于看到轨迹是如何裁剪搭接的。

creasson

给定A（-2, 1），B（-1/2, -1），C（3, -1），D（1/3, 1），P（x, y）的轨迹是:
-1000 - 200 x - 25015 x^2 - 100 x^3 + 120 x^4 + 200 y - 47990 x y - 4899 x^2 y + 24975 y^2 - 100 x y^2 + 240 x^2 y^2 - 4899 y^3 + 120 y^4 =0

wayne

hujunhua 发表于 2020-9-23 18:05
直接使用这个条件会漏掉一部分轨迹，还会多出一部分轨迹。
不如你在12楼的方法，能准确地得到所要的轨迹 ...

哈哈哈，按照老胡的条件，竟然瞬间就完美收工，一般方程出来了。四边形的边长是$a+b,b+c,c+d,d+a$,内接圆半径是$r$,P点坐标是${x,y}$，坐标原点在内接圆的圆心，四边形的四个顶点的坐标是
\[\left\{\frac{-a d^2+a r^2+2 d r^2}{d^2+r^2},\frac{2 a d r+d^2 r-r^3}{d^2+r^2}\right\},\left\{\frac{b c^2-b r^2-2 c r^2}{c^2+r^2},\frac{2 b c r+c^2 r-r^3}{c^2+r^2}\right\},\{-c,-r\},\{d,-r\}\]
隐含约束条件：$a b c+a b d+a c d+b c d=r^2 (a+b+c+d)$

画出来的图是一个三次方程和一个四次方程拼接起来的(两个方程在四边形的四个顶点处相交)，如下：
[说明，左图是拿上面的计算四个内心共圆的条件得到的最终轨迹图，右边是拿四边形的对顶角的角度和拼接计算而来的]

四边形外部的，就是$$两个角度和为0,\(\angle APB+\angle CPD =0\)。方程是关于$x,y$的三次多项式方程,如上图右图的蓝色线条。

1. -2 r (a d-r^2) x^3+r (2 a c d-a d^2+c d^2+a r^2-c r^2+2 d r^2) y^2+(-a d^2-c d^2+a r^2-c r^2+2 d r^2) y^3+x^2 (-r (2 a c d-a d^2+c d^2+a r^2-c r^2+2 d r^2)+(-a d^2-c d^2+a r^2-c r^2+2 d r^2) y)+x (-2 (a c d^2-a c r^2+2 a d r^2-2 c d r^2+d^2 r^2-r^4) y-2 r (a d-r^2) y^2)=0

复制代码

四边形内部的就是，\(\angle APB+\angle CPD =2\angle AEB\)，方程是关于$x,y$的四次多项式方程。,如上图右图的红色线条。

1. 4 (a-c) (a+c) r (a^2+r^2) (c^2+r^2) (d^2+r^2)^2 (2 a c d+a d^2+c d^2-a r^2-c r^2-2 d r^2)-2 r (12 a^4 c^3 d^3-8 a^3 c^4 d^3-4 a^2 c^5 d^3+2 a^5 c d^4+16 a^4 c^2 d^4+4 a^3 c^3 d^4-16 a^2 c^4 d^4-6 a c^5 d^4+a^5 d^5+2 a^4 c d^5+2 a^3 c^2 d^5-3 a c^4 d^5-2 c^5 d^5-2 a^4 d^6-4 a^3 c d^6+4 a c^3 d^6+2 c^4 d^6+12 a^4 c^3 d r^2+8 a^3 c^4 d r^2-4 a^2 c^5 d r^2+4 a^5 c d^2 r^2+12 a^4 c^2 d^2 r^2+24 a^3 c^3 d^2 r^2+28 a^2 c^4 d^2 r^2-4 a c^5 d^2 r^2+2 a^5 d^3 r^2+8 a^4 c d^3 r^2-12 a^3 c^2 d^3 r^2+56 a^2 c^3 d^3 r^2+42 a c^4 d^3 r^2+5 a^4 d^4 r^2+8 a^3 c d^4 r^2+14 a^2 c^2 d^4 r^2+24 a c^3 d^4 r^2+13 c^4 d^4 r^2+12 a^3 d^5 r^2+16 a^2 c d^5 r^2-4 a c^2 d^5 r^2-8 c^3 d^5 r^2+2 a^5 c r^4-4 a^4 c^2 r^4-12 a^3 c^3 r^4-4 a^2 c^4 r^4+2 a c^5 r^4+a^5 d r^4+6 a^4 c d r^4-30 a^3 c^2 d r^4-40 a^2 c^3 d r^4-3 a c^4 d r^4+2 c^5 d r^4+4 a^4 d^2 r^4+12 a^3 c d^2 r^4-28 a^2 c^2 d^2 r^4-76 a c^3 d^2 r^4-8 c^4 d^2 r^4+12 a^2 c d^3 r^4-40 a c^2 d^3 r^4-36 c^3 d^3 r^4-12 a^2 d^4 r^4-8 a c d^4 r^4+4 c^2 d^4 r^4-3 a^4 r^6+6 a^2 c^2 r^6-3 c^4 r^6-12 a^3 d r^6-4 a^2 c d r^6+12 a c^2 d r^6+4 c^3 d r^6-12 a^2 d^2 r^6-8 a c d^2 r^6+20 c^2 d^2 r^6) x^3-4 (a-c) (a+c) r (a c+a d+c d-r^2) (d^2+r^2) (2 a c d+a d^2+c d^2-a r^2-c r^2-2 d r^2) x^4+8 (a-c) (a+c) r^2 (d^2+r^2) (2 a c d+a d^2+c d^2-a r^2-c r^2-2 d r^2) (-2 a c^2 d+a^2 d^2-c^2 d^2+a^2 r^2+c^2 r^2-2 a d r^2+2 r^4) y+r (16 a^4 c^4 d^3-16 a^3 c^5 d^3+8 a^5 c^2 d^4+8 a^4 c^3 d^4+8 a^3 c^4 d^4-24 a^2 c^5 d^4+14 a^5 c d^5+8 a^4 c^2 d^5+4 a^3 c^3 d^5-8 a^2 c^4 d^5-18 a c^5 d^5+5 a^5 d^6+7 a^4 c d^6+2 a^3 c^2 d^6-2 a^2 c^3 d^6-7 a c^4 d^6-5 c^5 d^6+16 a^4 c^4 d r^2+16 a^3 c^5 d r^2+16 a^5 c^2 d^2 r^2+16 a^4 c^3 d^2 r^2+32 a^3 c^4 d^2 r^2+64 a^2 c^5 d^2 r^2+28 a^5 c d^3 r^2+32 a^4 c^2 d^3 r^2+8 a^3 c^3 d^3 r^2+80 a^2 c^4 d^3 r^2+44 a c^5 d^3 r^2+5 a^5 d^4 r^2-49 a^4 c d^4 r^2+26 a^3 c^2 d^4 r^2+70 a^2 c^3 d^4 r^2+65 a c^4 d^4 r^2+11 c^5 d^4 r^2-42 a^4 d^5 r^2-40 a^3 c d^5 r^2+36 a^2 c^2 d^5 r^2+56 a c^3 d^5 r^2+22 c^4 d^5 r^2-8 a^3 d^6 r^2-8 a^2 c d^6 r^2+8 a c^2 d^6 r^2+8 c^3 d^6 r^2+8 a^5 c^2 r^4+8 a^4 c^3 r^4-8 a^3 c^4 r^4-8 a^2 c^5 r^4+14 a^5 c d r^4+24 a^4 c^2 d r^4+36 a^3 c^3 d r^4-8 a^2 c^4 d r^4-34 a c^5 d r^4-5 a^5 d^2 r^4-55 a^4 c d^2 r^4+62 a^3 c^2 d^2 r^4+162 a^2 c^3 d^2 r^4-25 a c^4 d^2 r^4-11 c^5 d^2 r^4-20 a^4 d^3 r^4+64 a^3 c d^3 r^4+104 a^2 c^2 d^3 r^4+48 a c^3 d^3 r^4-4 c^4 d^3 r^4+88 a^3 d^4 r^4+56 a^2 c d^4 r^4-8 a c^2 d^4 r^4-8 c^3 d^4 r^4+16 a^2 d^5 r^4+16 a c d^5 r^4-5 a^5 r^6+a^4 c r^6+6 a^3 c^2 r^6-6 a^2 c^3 r^6-a c^4 r^6+5 c^5 r^6+22 a^4 d r^6+104 a^3 c d r^6-28 a^2 c^2 d r^6-104 a c^3 d r^6+6 c^4 d r^6+72 a^3 d^2 r^6+40 a^2 c d^2 r^6-88 a c^2 d^2 r^6-24 c^3 d^2 r^6-32 a^2 d^3 r^6+16 a c d^3 r^6+16 c^2 d^3 r^6-24 a^3 r^8-24 a^2 c r^8+24 a c^2 r^8+24 c^3 r^8-48 a^2 d r^8+48 c^2 d r^8) y^2+(4 a^5 c^2 d^4-4 a^4 c^3 d^4-4 a^3 c^4 d^4+4 a^2 c^5 d^4+4 a^5 c d^5-8 a^3 c^3 d^5+4 a c^5 d^5+a^5 d^6+a^4 c d^6-2 a^3 c^2 d^6-2 a^2 c^3 d^6+a c^4 d^6+c^5 d^6+8 a^5 c^2 d^2 r^2-40 a^3 c^4 d^2 r^2+8 a^5 c d^3 r^2-8 a^4 c^2 d^3 r^2-48 a^3 c^3 d^3 r^2-72 a^2 c^4 d^3 r^2-8 a c^5 d^3 r^2+a^5 d^4 r^2-45 a^4 c d^4 r^2-42 a^3 c^2 d^4 r^2-46 a^2 c^3 d^4 r^2-55 a c^4 d^4 r^2-5 c^5 d^4 r^2-22 a^4 d^5 r^2-40 a^3 c d^5 r^2-28 a^2 c^2 d^5 r^2-24 a c^3 d^5 r^2-14 c^4 d^5 r^2-4 a^3 d^6 r^2-12 a^2 c d^6 r^2-12 a c^2 d^6 r^2-4 c^3 d^6 r^2+4 a^5 c^2 r^4+4 a^4 c^3 r^4-4 a^3 c^4 r^4-4 a^2 c^5 r^4+4 a^5 c d r^4-8 a^4 c^2 d r^4+24 a^3 c^3 d r^4+24 a^2 c^4 d r^4-12 a c^5 d r^4-a^5 d^2 r^4-37 a^4 c d^2 r^4+2 a^3 c^2 d^2 r^4+138 a^2 c^3 d^2 r^4+31 a c^4 d^2 r^4-5 c^5 d^2 r^4-4 a^4 d^3 r^4+48 a^3 c d^3 r^4+56 a^2 c^2 d^3 r^4+80 a c^3 d^3 r^4+12 c^4 d^3 r^4+56 a^3 d^4 r^4+48 a^2 c d^4 r^4+8 a c^2 d^4 r^4+16 c^3 d^4 r^4+8 a^2 d^5 r^4+16 a c d^5 r^4+8 c^2 d^5 r^4-a^5 r^6+9 a^4 c r^6+10 a^3 c^2 r^6-10 a^2 c^3 r^6-9 a c^4 r^6+c^5 r^6+18 a^4 d r^6+88 a^3 c d r^6-12 a^2 c^2 d r^6-88 a c^3 d r^6-6 c^4 d r^6+44 a^3 d^2 r^6+44 a^2 c d^2 r^6-60 a c^2 d^2 r^6-28 c^3 d^2 r^6-24 a^2 d^3 r^6+16 a c d^3 r^6+8 c^2 d^3 r^6-16 a^3 r^8-16 a^2 c r^8+16 a c^2 r^8+16 c^3 r^8-32 a^2 d r^8+32 c^2 d r^8) y^3-4 (a-c) (a+c) r (a c+a d+c d-r^2) (d^2+r^2) (2 a c d+a d^2+c d^2-a r^2-c r^2-2 d r^2) y^4+x^2 (-r (16 a^4 c^4 d^3-16 a^3 c^5 d^3+8 a^5 c^2 d^4+8 a^4 c^3 d^4+8 a^3 c^4 d^4-24 a^2 c^5 d^4-2 a^5 c d^5-24 a^4 c^2 d^5+4 a^3 c^3 d^5+24 a^2 c^4 d^5-2 a c^5 d^5-3 a^5 d^6-17 a^4 c d^6-14 a^3 c^2 d^6+14 a^2 c^3 d^6+17 a c^4 d^6+3 c^5 d^6+16 a^4 c^4 d r^2+16 a^3 c^5 d r^2+16 a^5 c^2 d^2 r^2+16 a^4 c^3 d^2 r^2+32 a^3 c^4 d^2 r^2+64 a^2 c^5 d^2 r^2-4 a^5 c d^3 r^2+32 a^4 c^2 d^3 r^2+8 a^3 c^3 d^3 r^2+80 a^2 c^4 d^3 r^2+76 a c^5 d^3 r^2-3 a^5 d^4 r^2+23 a^4 c d^4 r^2+106 a^3 c^2 d^4 r^2-10 a^2 c^3 d^4 r^2-7 a c^4 d^4 r^2+19 c^5 d^4 r^2+6 a^4 d^5 r^2+56 a^3 c d^5 r^2+36 a^2 c^2 d^5 r^2-40 a c^3 d^5 r^2-26 c^4 d^5 r^2-8 a^3 d^6 r^2-8 a^2 c d^6 r^2+8 a c^2 d^6 r^2+8 c^3 d^6 r^2+8 a^5 c^2 r^4+8 a^4 c^3 r^4-8 a^3 c^4 r^4-8 a^2 c^5 r^4-2 a^5 c d r^4+56 a^4 c^2 d r^4+36 a^3 c^3 d r^4-40 a^2 c^4 d r^4-18 a c^5 d r^4+3 a^5 d^2 r^4+33 a^4 c d^2 r^4+142 a^3 c^2 d^2 r^4+82 a^2 c^3 d^2 r^4-113 a c^4 d^2 r^4-19 c^5 d^2 r^4+12 a^4 d^3 r^4+104 a^2 c^2 d^3 r^4+112 a c^3 d^3 r^4-36 c^4 d^3 r^4-8 a^3 d^4 r^4-40 a^2 c d^4 r^4+88 a c^2 d^4 r^4+88 c^3 d^4 r^4+16 a^2 d^5 r^4+16 a c d^5 r^4+3 a^5 r^6-7 a^4 c r^6-10 a^3 c^2 r^6+10 a^2 c^3 r^6+7 a c^4 r^6-3 c^5 r^6+6 a^4 d r^6-56 a^3 c d r^6-28 a^2 c^2 d r^6+56 a c^3 d r^6+22 c^4 d r^6+8 a^3 d^2 r^6-24 a^2 c d^2 r^6-24 a c^2 d^2 r^6+40 c^3 d^2 r^6+32 a^2 d^3 r^6+16 a c d^3 r^6-48 c^2 d^3 r^6+8 a^3 r^8+8 a^2 c r^8-8 a c^2 r^8-8 c^3 r^8+16 a^2 d r^8-16 c^2 d r^8)+(4 a^5 c^2 d^4-4 a^4 c^3 d^4-4 a^3 c^4 d^4+4 a^2 c^5 d^4+4 a^5 c d^5-8 a^3 c^3 d^5+4 a c^5 d^5+a^5 d^6+a^4 c d^6-2 a^3 c^2 d^6-2 a^2 c^3 d^6+a c^4 d^6+c^5 d^6+8 a^5 c^2 d^2 r^2-40 a^3 c^4 d^2 r^2+8 a^5 c d^3 r^2-8 a^4 c^2 d^3 r^2-48 a^3 c^3 d^3 r^2-72 a^2 c^4 d^3 r^2-8 a c^5 d^3 r^2+a^5 d^4 r^2-45 a^4 c d^4 r^2-42 a^3 c^2 d^4 r^2-46 a^2 c^3 d^4 r^2-55 a c^4 d^4 r^2-5 c^5 d^4 r^2-22 a^4 d^5 r^2-40 a^3 c d^5 r^2-28 a^2 c^2 d^5 r^2-24 a c^3 d^5 r^2-14 c^4 d^5 r^2-4 a^3 d^6 r^2-12 a^2 c d^6 r^2-12 a c^2 d^6 r^2-4 c^3 d^6 r^2+4 a^5 c^2 r^4+4 a^4 c^3 r^4-4 a^3 c^4 r^4-4 a^2 c^5 r^4+4 a^5 c d r^4-8 a^4 c^2 d r^4+24 a^3 c^3 d r^4+24 a^2 c^4 d r^4-12 a c^5 d r^4-a^5 d^2 r^4-37 a^4 c d^2 r^4+2 a^3 c^2 d^2 r^4+138 a^2 c^3 d^2 r^4+31 a c^4 d^2 r^4-5 c^5 d^2 r^4-4 a^4 d^3 r^4+48 a^3 c d^3 r^4+56 a^2 c^2 d^3 r^4+80 a c^3 d^3 r^4+12 c^4 d^3 r^4+56 a^3 d^4 r^4+48 a^2 c d^4 r^4+8 a c^2 d^4 r^4+16 c^3 d^4 r^4+8 a^2 d^5 r^4+16 a c d^5 r^4+8 c^2 d^5 r^4-a^5 r^6+9 a^4 c r^6+10 a^3 c^2 r^6-10 a^2 c^3 r^6-9 a c^4 r^6+c^5 r^6+18 a^4 d r^6+88 a^3 c d r^6-12 a^2 c^2 d r^6-88 a c^3 d r^6-6 c^4 d r^6+44 a^3 d^2 r^6+44 a^2 c d^2 r^6-60 a c^2 d^2 r^6-28 c^3 d^2 r^6-24 a^2 d^3 r^6+16 a c d^3 r^6+8 c^2 d^3 r^6-16 a^3 r^8-16 a^2 c r^8+16 a c^2 r^8+16 c^3 r^8-32 a^2 d r^8+32 c^2 d r^8) y-8 (a-c) (a+c) r (a c+a d+c d-r^2) (d^2+r^2) (2 a c d+a d^2+c d^2-a r^2-c r^2-2 d r^2) y^2)+x (8 (a-c) (a+c) r (d^2+r^2) (2 a c d+a d^2+c d^2-a r^2-c r^2-2 d r^2) (a^2 c d^2+a c^2 d^2+a^2 c r^2-a c^2 r^2-2 c^2 d r^2+a d^2 r^2+c d^2 r^2-a r^4+c r^4-2 d r^4)+2 (4 a^5 c^3 d^4-8 a^4 c^4 d^4+4 a^3 c^5 d^4+4 a^5 c^2 d^5-4 a^4 c^3 d^5-4 a^3 c^4 d^5+4 a^2 c^5 d^5+a^5 c d^6-2 a^3 c^3 d^6+a c^5 d^6+8 a^5 c^3 d^2 r^2-24 a^3 c^5 d^2 r^2+8 a^5 c^2 d^3 r^2-8 a^4 c^3 d^3 r^2-8 a^3 c^4 d^3 r^2-56 a^2 c^5 d^3 r^2-3 a^5 c d^4 r^2-44 a^4 c^2 d^4 r^2-2 a^3 c^3 d^4 r^2-12 a^2 c^4 d^4 r^2-35 a c^5 d^4 r^2-2 a^5 d^5 r^2-14 a^4 c d^5 r^2-36 a^3 c^2 d^5 r^2-12 a^2 c^3 d^5 r^2+6 a c^4 d^5 r^2-6 c^5 d^5 r^2+5 a^4 d^6 r^2-4 a^3 c d^6 r^2-18 a^2 c^2 d^6 r^2-4 a c^3 d^6 r^2+5 c^4 d^6 r^2+4 a^5 c^3 r^4+8 a^4 c^4 r^4+4 a^3 c^5 r^4+4 a^5 c^2 d r^4-4 a^4 c^3 d r^4+28 a^3 c^4 d r^4+36 a^2 c^5 d r^4-9 a^5 c d^2 r^4-40 a^4 c^2 d^2 r^4-14 a^3 c^3 d^2 r^4+88 a^2 c^4 d^2 r^4+55 a c^5 d^2 r^4-4 a^5 d^3 r^4-28 a^4 c d^3 r^4-8 a^3 c^2 d^3 r^4-56 a^2 c^3 d^3 r^4+76 a c^4 d^3 r^4+20 c^5 d^3 r^4-15 a^4 d^4 r^4-24 a^3 c d^4 r^4-34 a^2 c^2 d^4 r^4-24 a c^3 d^4 r^4+17 c^4 d^4 r^4-36 a^3 d^5 r^4-28 a^2 c d^5 r^4+4 a c^2 d^5 r^4-4 c^3 d^5 r^4-4 a^2 d^6 r^4-8 a c d^6 r^4-4 c^2 d^6 r^4-5 a^5 c r^6+4 a^4 c^2 r^6+18 a^3 c^3 r^6+4 a^2 c^4 r^6-5 a c^5 r^6-2 a^5 d r^6-14 a^4 c d r^6+60 a^3 c^2 d r^6+52 a^2 c^3 d r^6-26 a c^4 d r^6-6 c^5 d r^6-13 a^4 d^2 r^6-20 a^3 c d^2 r^6+66 a^2 c^2 d^2 r^6+76 a c^3 d^2 r^6-13 c^4 d^2 r^6-8 a^3 d^3 r^6-24 a^2 c d^3 r^6+72 a c^2 d^3 r^6+24 c^3 d^3 r^6+24 a^2 d^4 r^6-8 c^2 d^4 r^6+7 a^4 r^8-14 a^2 c^2 r^8+7 c^4 r^8+28 a^3 d r^8+4 a^2 c d r^8-28 a c^2 d r^8-4 c^3 d r^8+28 a^2 d^2 r^8+8 a c d^2 r^8-36 c^2 d^2 r^8) y-2 r (12 a^4 c^3 d^3-8 a^3 c^4 d^3-4 a^2 c^5 d^3+2 a^5 c d^4+16 a^4 c^2 d^4+4 a^3 c^3 d^4-16 a^2 c^4 d^4-6 a c^5 d^4+a^5 d^5+2 a^4 c d^5+2 a^3 c^2 d^5-3 a c^4 d^5-2 c^5 d^5-2 a^4 d^6-4 a^3 c d^6+4 a c^3 d^6+2 c^4 d^6+12 a^4 c^3 d r^2+8 a^3 c^4 d r^2-4 a^2 c^5 d r^2+4 a^5 c d^2 r^2+12 a^4 c^2 d^2 r^2+24 a^3 c^3 d^2 r^2+28 a^2 c^4 d^2 r^2-4 a c^5 d^2 r^2+2 a^5 d^3 r^2+8 a^4 c d^3 r^2-12 a^3 c^2 d^3 r^2+56 a^2 c^3 d^3 r^2+42 a c^4 d^3 r^2+5 a^4 d^4 r^2+8 a^3 c d^4 r^2+14 a^2 c^2 d^4 r^2+24 a c^3 d^4 r^2+13 c^4 d^4 r^2+12 a^3 d^5 r^2+16 a^2 c d^5 r^2-4 a c^2 d^5 r^2-8 c^3 d^5 r^2+2 a^5 c r^4-4 a^4 c^2 r^4-12 a^3 c^3 r^4-4 a^2 c^4 r^4+2 a c^5 r^4+a^5 d r^4+6 a^4 c d r^4-30 a^3 c^2 d r^4-40 a^2 c^3 d r^4-3 a c^4 d r^4+2 c^5 d r^4+4 a^4 d^2 r^4+12 a^3 c d^2 r^4-28 a^2 c^2 d^2 r^4-76 a c^3 d^2 r^4-8 c^4 d^2 r^4+12 a^2 c d^3 r^4-40 a c^2 d^3 r^4-36 c^3 d^3 r^4-12 a^2 d^4 r^4-8 a c d^4 r^4+4 c^2 d^4 r^4-3 a^4 r^6+6 a^2 c^2 r^6-3 c^4 r^6-12 a^3 d r^6-4 a^2 c d r^6+12 a c^2 d r^6+4 c^3 d r^6-12 a^2 d^2 r^6-8 a c d^2 r^6+20 c^2 d^2 r^6) y^2)=0

复制代码

数学星空

\(a = \frac{3}{2}, b = \frac{3}{11}, c = 2, d = 1, r = 1\)

924000*x^4 + 1848000*x^2*y^2 + 913352*y^4 - 7668750*x^3 - 16807500*x^2*y - 7668750*x*y^2 - 16807500*y^3 - 66768000*x^2 + 11809500*x*y + 65928000*y^2 - 1008000*x + 2866648*y - 5460000=0