圆外切四边形的四内心共圆问题

dlsh

四点共圆判定公式和内心表达式

图片中的复斜率就是签名链接中的共轭比，详细内容参考签名链接。

wayne

wayne 发表于 2020-9-23 18:52
哈哈哈，按照老胡的条件，竟然瞬间就完美收工，一般方程出来了。四边形的边长是$a+b,b+c,c+d,d+a$,内接圆 ...

代码是半手工的。我就不整理了。先分别算出 两段曲线的方程，再Factor一下因式，手工提取分子中的非平凡项

1. {pA,pB,pC,pD,pE}={{(-a d^2+a r^2+2 d r^2)/(d^2+r^2),(2 a d r+d^2 r-r^3)/(d^2+r^2)},{(b c^2-b r^2-2 c r^2)/(c^2+r^2),(2 b c r+c^2 r-r^3)/(c^2+r^2)},{-c,-r},{d,-r},{x,y}};
   
2. g2[{x_,y_},{x1_,y1_},{x2_,y2_}]:=(y-y1)(x1-x2)-(y1-y2)(x-x1);
   
3. tan\[Theta][{x1_,y1_},{x2_,y2_}]:=(y1-y2)/(x1-x2);
   
4. crossangle[{x1_,y1_},{x2_,y2_},{x3_,y3_}]:=(tan\[Theta][{x3,y3},{x2,y2}]-tan\[Theta][{x1,y1},{x2,y2}])/(1+tan\[Theta][{x3,y3},{x2,y2}]*tan\[Theta][{x1,y1},{x2,y2}]);
   
5. o={x,y}/.First[Solve[{g2[{x,y},pA,pC]==0,g2[{x,y},pB,pD]==0},{x,y}]];
   
6. eqs1=(2 (tan\[Theta][pB,o]-tan\[Theta][pA,o])/(1+tan\[Theta][pA,o]*tan\[Theta][pB,o]))/(1-((tan\[Theta][pA,o]-tan\[Theta][pB,o])/(1+tan\[Theta][pA,o]*tan\[Theta][pB,o]))^2)-(crossangle[pA,pE,pB]+crossangle[pC,pE,pD])/(1-crossangle[pA,pE,pB]*crossangle[pC,pE,pD]);
   
7. eqs2 = crossangle[pA, pE, pB] + crossangle[pC, pE, pD] // Factor

复制代码

然后根据$a b c + a b d + a c d + b c d - a r^2 - b r^2 - c r^2 - d r^2=0$恒成立，用GroebnerBasis化简，找出项最少的表达式。不过意义不大，因为如果给定$a,b,c,d,r$的值的话，最后都是一样的表达式。

1. ans=GroebnerBasis[{tmp==0,a b c+a b d+a c d+b c d-a r^2-b r^2-c r^2-d r^2==0},{x,y}];Table[{i,Length[MonomialList[ans[[i]]]]},{i,Length[ans]}]

复制代码

hujunhua

现在也许可以比较全面地回答这个问题了：
1、记对角线交点为E，P在外切四边形内时，应满足 ∠APB+∠CPD=2∠AEB; 这包括对角线交点E、两对角线中垂线的交点、四边形的4个顶点。（9#），轨迹是一个四次曲线在四边形内的一部分（19#）
2、P在外切四边形外时，应满足 ∠APB=∠CPD；这包括四边形的对边交点（两个）、四边形的4个顶点。（9#），轨迹是一个三次曲线在在四边形外的一部分(该曲线还二次经过内切圆的圆心)（19#）
3、P在外切四边形的边上，恒成立（wayne的贡献，12#），即轨迹是四条线段。

所以，现在还能回答为什么前面最开始代数计算的时候化简这么麻烦，因为这里涉及到六个分段函数，四条直线，一个三次曲线，一个四次曲线。
如图：
\[{a,b,c,d,r}=\left\{1,\frac{7}{17},\frac{3}{2},\frac{3}{2},1\right\}\]
\[\left\{\text{A},\left\{\frac{7}{13},\frac{17}{13}\right\}\right\},\left\{\text{B},\left\{-\frac{13}{17},\frac{13}{17}\right\}\right\},\left\{\text{C},\left\{-\frac{3}{2},-1\right\}\right\},\left\{\text{D},\left\{\frac{3}{2},-1\right\}\right\},\left\{\text{E},\left\{-\frac{18}{65},\frac{5}{13}\right\}\right\},\{\text{F},\{-5,-1\}\},\left\{\text{G},\left\{0,\frac{13}{5}\right\}\right\}\]


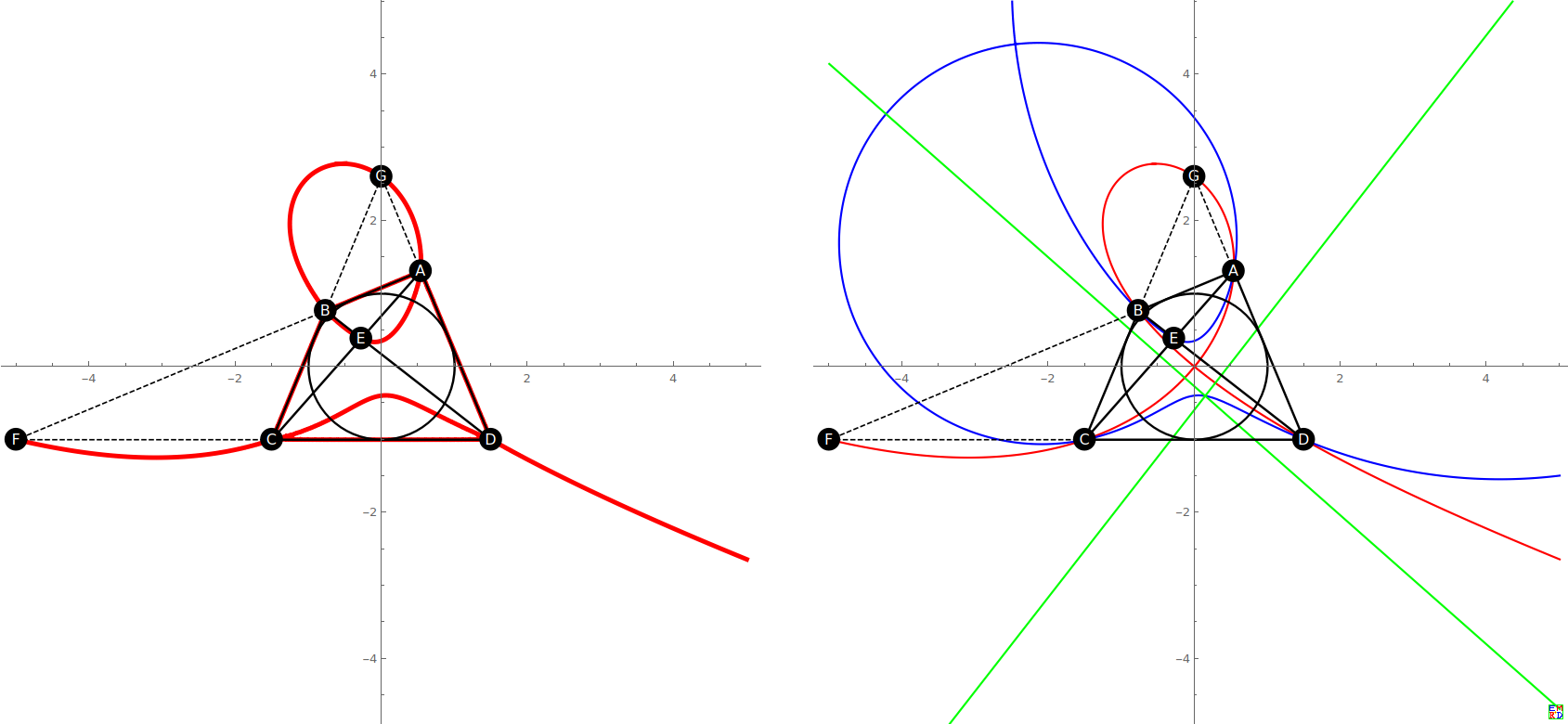
画图代码如下[增加了计算$F,G$两点，如果$F,G$在无穷远处，代码将报错，暂时不处理了]：

1. cc[{x_,y_}]:={x^2+y^2,x,y,1};
   
2. g2[{x_,y_},{x1_,y1_},{x2_,y2_}]:=(y-y1)(x1-x2)-(y1-y2)(x-x1);
   
3. vertical[{x_,y_},{x1_,y1_},{x2_,y2_}]:=(x-(x1+x2)/2)(x1-x2)+(y-(y1+y2)/2)(y1-y2)
   
4. tan\[Theta][{x1_,y1_},{x2_,y2_}]:=(y1-y2)/(x1-x2);
   
5. crossangle[{x1_,y1_},{x2_,y2_},{x3_,y3_}]:=(tan\[Theta][{x2,y2},{x3,y3}]-tan\[Theta][{x1,y1},{x2,y2}])/(1+tan\[Theta][{x1,y1},{x2,y2}]*tan\[Theta][{x2,y2},{x3,y3}]);
   
6. Block[{a=1,b,c=3/2,d=3/2,r=1,n=5,pA,pB,pC,pD},temp={{Subscript[x,A],Subscript[y,A]},{Subscript[x,B],Subscript[y,B]},{-c,-r},{d,-r}};
   
7. b=(-a c d+a r^2+c r^2+d r^2)/(a c+a d+c d-r^2);
   
8. pP={x,y};
   
9. sol=Solve[{Total[pA^2]==a^2+r^2,Total[pB^2]==b^2+r^2,Total[(pB-pC)^2]==(b+c)^2,Total[(pD-pA)^2]==(d+a)^2,Subscript[y,A]!=-r,Subscript[y,B]!=-r}/.Thread[{pA,pB,pC,pD}->temp],{Subscript[x,A],Subscript[y,A],Subscript[x,B],Subscript[y,B]}];
   
10. {pA,pB,pC,pD}=temp/.sol[[1]];
    
11. pE={x,y}/.Quiet[First[Solve[{g2[pP,pA,pC]==0,g2[pP,pB,pD]==0},{x,y}]]];
    
12. pF={x,y}/.Quiet[First[Solve[{g2[pP,pA,pB]==0,g2[pP,pC,pD]==0},{x,y}]]];
    
13. pG={x,y}/.Quiet[First[Solve[{g2[pP,pA,pD]==0,g2[pP,pB,pC]==0},{x,y}]]];
    
14. pts=Transpose[{Characters["ABCDEFG"],{pA,pB,pC,pD,pE,pF,pG}}];
    
15. Print[{a,b,c,d,r}];Print[pts];
    
16. I4=Total/@{{be pA,ae pB,(a+b) pP}/(be+ae+(a+b)),{(c+b) pP,ce pB,be pC}/((c+b)+ce+be),{(c+d) pP,de pC,ce pD}/((c+d)+de+ce),{(a+d) pP,de pA,ae pD}/((a+d)+de+ae)}/.{ae->Norm[pA-pP],be->Norm[pB-pP],ce->Norm[pC-pP],de->Norm[pD-pP]};
    
17. eqs1=(2 (tan\[Theta][pB,pE]-tan\[Theta][pA,pE])/(1+tan\[Theta][pA,pE]*tan\[Theta][pB,pE]))/(1-((tan\[Theta][pA,pE]-tan\[Theta][pB,pE])/(1+tan\[Theta][pA,pE]*tan\[Theta][pB,pE]))^2)-(crossangle[pA,pP,pB]+crossangle[pC,pP,pD])/(1-crossangle[pA,pP,pB]*crossangle[pC,pP,pD]);
    
18. eqs2=crossangle[pA,pP,pB]+crossangle[pC,pP,pD];
    
19. GraphicsRow[{Show[{ContourPlot[Det[cc/@I4]==0,{x,-n,n},{y,-n,n},PlotPoints->100,ContourStyle->{Red,Thickness[0.006]},Axes->True,Frame->False],Graphics[{Thickness[0.003],Circle[],Black,Line[Subsets[pts[[1;;4,2]],{2}]],Thickness[0.002],Dashed,Line[{{pB,pF},{pC,pF},{pA,pG},{pB,pG}}],PointSize[.03],Point[pts[[All,2]]],Table[Text[Style[p[[1]],White,12],p[[2]]],{p,pts}]},Axes->True,Frame->False]}],Show[{ContourPlot[{eqs1==0,eqs2==0,vertical[{x,y},pA,pC]==0,vertical[{x,y},pB,pD]==0},{x,-n,n},{y,-n,n},PlotPoints->100,ContourStyle->{Red,Blue,Green,Green},Axes->True,Frame->False],Graphics[{Thickness[0.003],Circle[],Black,Line[Subsets[pts[[1;;4,2]],{2}]],Thickness[0.002],Dashed,Line[{{pB,pF},{pC,pF},{pA,pG},{pB,pG}}],PointSize[.03],Point[pts[[All,2]]],Table[Text[Style[p[[1]],White,12],p[[2]]],{p,pts}]},Axes->True,Frame->False]}]}]]

复制代码

creasson

前述分析基于已探索结论确定了曲线的形状，现在考虑直接地求解。
令$Z(u,v)=\frac{1-u v}{1+u v}+\frac{(u+v)}{1+u v}i$，$A=Z(a,b),B=Z(b,-1),C=Z(c,-1),D=Z(c,a)$，其中$a>0,b<-\frac{1}{a}<c<1$，如此$ABCD$是外切于单位圆，且$BC$平行于$x$轴的逆时针四边形。
然后令$$ \mathop {AP}\limits^ \to   = \frac{\left( s + t \right)\left( 1 - st \right)}{s\left( 1 - it \right)^2} \mathop {AB}\limits^ \to , \mathop {CP}\limits^ \to   = \frac{\left( p + q \right)\left( 1 - pq \right)}{p\left( 1 - iq \right)^2} \mathop {CD}\limits^ \to  $$
也可设出$P$的坐标后反解出$s,t,p,q$:
\[P = \frac{{( - i + b)((1 + i)s + (1 + i)abs + t + at + ibt + iabt + 2st + 2iast - 2bst - 2iabst - {s^2}t - a{s^2}t - ib{s^2}t - iab{s^2}t - (1 + i)s{t^2} - (1 + i)abs{t^2})}}{{( - 1 + b)(1 + ab)s{{(i + t)}^2}}}\]
\[P = \frac{{( - i + c)(ip - ap - icp + acp - q - aq - icq - iacq + (2 - 2i)pq + (2 - 2i)acpq + {p^2}q + a{p^2}q + ic{p^2}q + iac{p^2}q - ip{q^2} + ap{q^2} + icp{q^2} - acp{q^2})}}{{( - 1 + c)(1 + ac)p{{(i + q)}^2}}}\]
这样三角形$APB,BPC,CPD,DPA$的内心均可有理表示：
\[\mathop {PI_1}\limits^ \to   =  - \frac{{(1 + a){{( - i + b)}^2}( - i + s)t( - 1 + st)}}{{( - 1 + b)(1 + ab)s{{(i + t)}^2}}}\]
$PI_2$=((-I + b) (-I + c) (-I + s) (p s + a p s + b p s + a^2 b p s +
     a b^2 p s - a^2 b^2 p s - 2 c p s + 2 a^2 b^2 c p s + c^2 p s -
     a c^2 p s - b c^2 p s - a^2 b c^2 p s - a b^2 c^2 p s -
     a^2 b^2 c^2 p s + q s + a q s - b q s + a^2 b q s - a b^2 q s -
     a^2 b^2 q s + c^2 q s + a c^2 q s - b c^2 q s + a^2 b c^2 q s -
     a b^2 c^2 q s - a^2 b^2 c^2 q s - p^2 q s - a p^2 q s +
     b p^2 q s - a^2 b p^2 q s + a b^2 p^2 q s + a^2 b^2 p^2 q s -
     c^2 p^2 q s - a c^2 p^2 q s + b c^2 p^2 q s - a^2 b c^2 p^2 q s +
      a b^2 c^2 p^2 q s + a^2 b^2 c^2 p^2 q s - p q^2 s - a p q^2 s +
     3 b p q^2 s - a^2 b p q^2 s + 3 a b^2 p q^2 s +
     a^2 b^2 p q^2 s - 2 c p q^2 s + 2 a^2 b^2 c p q^2 s -
     c^2 p q^2 s - 3 a c^2 p q^2 s + b c^2 p q^2 s -
     3 a^2 b c^2 p q^2 s + a b^2 c^2 p q^2 s + a^2 b^2 c^2 p q^2 s -
     p t - a p t - b^2 p t - a b^2 p t + c p t - a^2 c p t +
     b^2 c p t - a^2 b^2 c p t + a c^2 p t + a^2 c^2 p t +
     a b^2 c^2 p t + a^2 b^2 c^2 p t - p q^2 t - a p q^2 t -
     b^2 p q^2 t - a b^2 p q^2 t + c p q^2 t - a^2 c p q^2 t +
     b^2 c p q^2 t - a^2 b^2 c p q^2 t + a c^2 p q^2 t +
     a^2 c^2 p q^2 t + a b^2 c^2 p q^2 t + a^2 b^2 c^2 p q^2 t -
     p s^2 t - a p s^2 t - b^2 p s^2 t - a b^2 p s^2 t + c p s^2 t -
     a^2 c p s^2 t + b^2 c p s^2 t - a^2 b^2 c p s^2 t +
     a c^2 p s^2 t + a^2 c^2 p s^2 t + a b^2 c^2 p s^2 t +
     a^2 b^2 c^2 p s^2 t - p q^2 s^2 t - a p q^2 s^2 t -
     b^2 p q^2 s^2 t - a b^2 p q^2 s^2 t + c p q^2 s^2 t -
     a^2 c p q^2 s^2 t + b^2 c p q^2 s^2 t - a^2 b^2 c p q^2 s^2 t +
     a c^2 p q^2 s^2 t + a^2 c^2 p q^2 s^2 t + a b^2 c^2 p q^2 s^2 t +
      a^2 b^2 c^2 p q^2 s^2 t + p s t^2 + a p s t^2 + b p s t^2 +
     a^2 b p s t^2 + a b^2 p s t^2 - a^2 b^2 p s t^2 - 2 c p s t^2 +
     2 a^2 b^2 c p s t^2 + c^2 p s t^2 - a c^2 p s t^2 -
     b c^2 p s t^2 - a^2 b c^2 p s t^2 - a b^2 c^2 p s t^2 -
     a^2 b^2 c^2 p s t^2 + q s t^2 + a q s t^2 - b q s t^2 +
     a^2 b q s t^2 - a b^2 q s t^2 - a^2 b^2 q s t^2 + c^2 q s t^2 +
     a c^2 q s t^2 - b c^2 q s t^2 + a^2 b c^2 q s t^2 -
     a b^2 c^2 q s t^2 - a^2 b^2 c^2 q s t^2 - p^2 q s t^2 -
     a p^2 q s t^2 + b p^2 q s t^2 - a^2 b p^2 q s t^2 +
     a b^2 p^2 q s t^2 + a^2 b^2 p^2 q s t^2 - c^2 p^2 q s t^2 -
     a c^2 p^2 q s t^2 + b c^2 p^2 q s t^2 - a^2 b c^2 p^2 q s t^2 +
     a b^2 c^2 p^2 q s t^2 + a^2 b^2 c^2 p^2 q s t^2 - p q^2 s t^2 -
     a p q^2 s t^2 + 3 b p q^2 s t^2 - a^2 b p q^2 s t^2 +
     3 a b^2 p q^2 s t^2 + a^2 b^2 p q^2 s t^2 - 2 c p q^2 s t^2 +
     2 a^2 b^2 c p q^2 s t^2 - c^2 p q^2 s t^2 - 3 a c^2 p q^2 s t^2 +
      b c^2 p q^2 s t^2 - 3 a^2 b c^2 p q^2 s t^2 +
     a b^2 c^2 p q^2 s t^2 + a^2 b^2 c^2 p q^2 s t^2))/(2 (-1 +
     b) (1 + a b) (-1 + c) (1 + a c) p (I + q) s (I + t) (1 + b c +
     b q - c q - b s + c s + q s + b c q s - b t + c t + q t +
     b c q t - s t - b c s t - b q s t + c q s t))

\[\mathop {P{I_3}}\limits^ \to   = \frac{{(1 + a){{( - i + c)}^2}( - i + p)q( - 1 + pq)}}{{( - 1 + c)(1 + ac)p{{(i + q)}^2}}}\]

$PI_4$=((-I + b) (-I + c) (-I + p) (p s + a p s + b p s + a^2 b p s +
     a b^2 p s - a^2 b^2 p s - 2 c p s + 2 a^2 b^2 c p s + c^2 p s -
     a c^2 p s - b c^2 p s - a^2 b c^2 p s - a b^2 c^2 p s -
     a^2 b^2 c^2 p s - q s - a q s + b q s - a^2 b q s + a b^2 q s +
     a^2 b^2 q s - c^2 q s - a c^2 q s + b c^2 q s - a^2 b c^2 q s +
     a b^2 c^2 q s + a^2 b^2 c^2 q s - p^2 q s - a p^2 q s +
     b p^2 q s - a^2 b p^2 q s + a b^2 p^2 q s + a^2 b^2 p^2 q s -
     c^2 p^2 q s - a c^2 p^2 q s + b c^2 p^2 q s - a^2 b c^2 p^2 q s +
      a b^2 c^2 p^2 q s + a^2 b^2 c^2 p^2 q s + p q^2 s + a p q^2 s +
     b p q^2 s + a^2 b p q^2 s + a b^2 p q^2 s - a^2 b^2 p q^2 s -
     2 c p q^2 s + 2 a^2 b^2 c p q^2 s + c^2 p q^2 s - a c^2 p q^2 s -
      b c^2 p q^2 s - a^2 b c^2 p q^2 s - a b^2 c^2 p q^2 s -
     a^2 b^2 c^2 p q^2 s + p t + a p t + b^2 p t + a b^2 p t - c p t +
      a^2 c p t - b^2 c p t + a^2 b^2 c p t - a c^2 p t -
     a^2 c^2 p t - a b^2 c^2 p t - a^2 b^2 c^2 p t + p q^2 t +
     a p q^2 t + b^2 p q^2 t + a b^2 p q^2 t - c p q^2 t +
     a^2 c p q^2 t - b^2 c p q^2 t + a^2 b^2 c p q^2 t -
     a c^2 p q^2 t - a^2 c^2 p q^2 t - a b^2 c^2 p q^2 t -
     a^2 b^2 c^2 p q^2 t - p s^2 t - a p s^2 t - b^2 p s^2 t -
     a b^2 p s^2 t + c p s^2 t - a^2 c p s^2 t + b^2 c p s^2 t -
     a^2 b^2 c p s^2 t + a c^2 p s^2 t + a^2 c^2 p s^2 t +
     a b^2 c^2 p s^2 t + a^2 b^2 c^2 p s^2 t - p q^2 s^2 t -
     a p q^2 s^2 t - b^2 p q^2 s^2 t - a b^2 p q^2 s^2 t +
     c p q^2 s^2 t - a^2 c p q^2 s^2 t + b^2 c p q^2 s^2 t -
     a^2 b^2 c p q^2 s^2 t + a c^2 p q^2 s^2 t + a^2 c^2 p q^2 s^2 t +
      a b^2 c^2 p q^2 s^2 t + a^2 b^2 c^2 p q^2 s^2 t - p s t^2 -
     a p s t^2 + b p s t^2 + a^2 b p s t^2 - 2 b^2 p s t^2 -
     a b^2 p s t^2 - a^2 b^2 p s t^2 - 2 a^2 c p s t^2 +
     2 b^2 c p s t^2 + c^2 p s t^2 + a c^2 p s t^2 +
     2 a^2 c^2 p s t^2 - b c^2 p s t^2 - a^2 b c^2 p s t^2 +
     a b^2 c^2 p s t^2 + a^2 b^2 c^2 p s t^2 - q s t^2 - a q s t^2 +
     b q s t^2 - a^2 b q s t^2 + a b^2 q s t^2 + a^2 b^2 q s t^2 -
     c^2 q s t^2 - a c^2 q s t^2 + b c^2 q s t^2 - a^2 b c^2 q s t^2 +
      a b^2 c^2 q s t^2 + a^2 b^2 c^2 q s t^2 - p^2 q s t^2 -
     a p^2 q s t^2 + b p^2 q s t^2 - a^2 b p^2 q s t^2 +
     a b^2 p^2 q s t^2 + a^2 b^2 p^2 q s t^2 - c^2 p^2 q s t^2 -
     a c^2 p^2 q s t^2 + b c^2 p^2 q s t^2 - a^2 b c^2 p^2 q s t^2 +
     a b^2 c^2 p^2 q s t^2 + a^2 b^2 c^2 p^2 q s t^2 - p q^2 s t^2 -
     a p q^2 s t^2 + b p q^2 s t^2 + a^2 b p q^2 s t^2 -
     2 b^2 p q^2 s t^2 - a b^2 p q^2 s t^2 - a^2 b^2 p q^2 s t^2 -
     2 a^2 c p q^2 s t^2 + 2 b^2 c p q^2 s t^2 + c^2 p q^2 s t^2 +
     a c^2 p q^2 s t^2 + 2 a^2 c^2 p q^2 s t^2 - b c^2 p q^2 s t^2 -
     a^2 b c^2 p q^2 s t^2 + a b^2 c^2 p q^2 s t^2 +
     a^2 b^2 c^2 p q^2 s t^2))/(2 (-1 + b) (1 + a b) (-1 + c) (1 +
     a c) p (I + q) s (I + t) (-1 - b c - b p + c p - b q + c q +
     p q + b c p q + b t - c t - p t - b c p t - q t - b c q t -
     b p q t + c p q t))
四内心共圆的条件为：\[{\mathop{\rm Im}\nolimits} \left( {\frac{{\mathop {P{I_1}}\limits^ \to   - \mathop {P{I_3}}\limits^ \to  }}{{\mathop {P{I_2}}\limits^ \to   - \mathop {P{I_3}}\limits^ \to  }}\frac{{\mathop {P{I_2}}\limits^ \to   - \mathop {P{I_4}}\limits^ \to  }}{{\mathop {P{I_1}}\limits^ \to   - \mathop {P{I_4}}\limits^ \to  }}} \right) = 0\]
代入，理论上可以由此得到$P$的轨迹方程，对于给定的$a,b,c$也确实可以求解出。
但是，直接计算会产生两个数十万项的多项式相乘，根本无法计算，
我现在尝试不断利用$s,t,p,q$之间的关系来将关系式化简为关于$s,t$的多项式方程，目前仍看不到可以得到最终式子的希望。
当然，如果直接指定$P$的位置，化简会容易得多。

hujunhua

已知：四边形ABCD是一个镖形（AB＝BC，CD＝DA），O是其内心，F是劣弧AOC上一点。
求证：        1、∠BFC+∠DFA＝180°。
                2、△AFB，△BFC，△CFD，△DFA的内心四点共圆。

镖形的还有F点位于对称轴上和优弧上的情况，但劣弧上是重点。

creasson

又尝试了两种方法，先说第一种:
点$A,B,C,D$的设法仍如24#，$P=x+y*I$,  然后再令$PA=s,PB=t,PC=p,PD=q$, 根据重心坐标性质,  有
\[{I_1} = \frac{{AB \bullet P + PA \bullet B + PB \bullet A}}{{AB \bullet P + PA \bullet B + PB \bullet A}} =  - \frac{{( - i + b)((1 + i)s + (1 + i)abs + it - at - ibt + abt - ix - iax - bx - abx + y + ay - iby - iaby)}}{{1 + a + {b^2} + a{b^2} - s + bs - abs + a{b^2}s - t + bt - abt + a{b^2}t}}\]
另外三个内心同理可表示。
然后代入四点共圆条件
\[{\mathop{\rm Im}\nolimits} \left( {\frac{{{I_1} - {I_3}}}{{{I_2} - {I_3}}}\frac{{{I_2} - {I_4}}}{{{I_1} - {I_4}}}} \right) = 0\]
再利用$s,t,p,q$的等式
\[{s^2} - P{A^2} = \frac{{ - 1 - {a^2} - {b^2} - {a^2}{b^2} + {s^2} + 2ab{s^2} + {a^2}{b^2}{s^2} + 2x - 2{a^2}{b^2}x - {x^2} - 2ab{x^2} - {a^2}{b^2}{x^2} + 2ay + 2by + 2{a^2}by + 2a{b^2}y - {y^2} - 2ab{y^2} - {a^2}{b^2}{y^2}}}{{{{(1 + ab)}^2}}} = 0\]
...
不断求余降次，最后得到这样的式子，关于$s,t,p,q$均是一次的
\[{f_1}stpq + {f_2}stp + {f_3}tpq + ... + {f_{12}}s + {f_{13}}t + {f_{14}}p + {f_{15}}q + {f_{16}} = 0\]
总项数为几十万之巨，虽然理论上可用$s,t,p,q$分别乘上式再化简转化为线性方程组消去参数，但实际已经没法计算了。

creasson

第二种，我们直接设出四内心的坐标：$I_k = p_k + q_ki,\left( k = 1,2,3,4 \right)$。
然后利用marden定理的一般形式，对复平面上的任意不共线三点$z_1,z_2,z_3 $, 其内切椭圆之焦点$z$满足方程：
\[\left( {z - {z_1}} \right)\left( {z - {z_1}} \right) + \lambda \left( {z - {z_2}} \right)\left( {z - {z_3}} \right) + \mu \left( {z - {z_3}} \right)\left( {z - {z_1}} \right) = 0\]
其中$\lambda ,\mu$是实数 ,对于内切圆来说，两个焦点是重合的，故而还有上式的微分等于0，也即
\[2\left( {1 + \lambda  + \mu } \right)z - \left( {{z_1} + {z_2} + \lambda {z_2} + \lambda {z_3} + \mu {z_3} + \mu {z_1}} \right) = 0\]
代入各点表示式求解出$\lambda ,\mu$
根据其虚部为0的条件，可得两个等式，并可将其中一个变量$q$用另一个变量$p$的分式形式表示出来, $p$满足一个四次方程。
然后代入共圆条件化简。

wayne

creasson 发表于 2020-9-26 11:22
又尝试了两种方法，先说第一种:
点$A,B,C,D$的设法仍如24#，$P=x+y*I$,  然后再令$PA=s,PB=t,PC=p,PD=q$,  ...

在23楼有大致说明，因为 通过执果索因，我们知道，目标表达式是六个多项式的分段函数，其中四个是二元一次多项式，一个是二元三次多项式，一个是二元四次多项式，
分段的情况只能通过平方消除，于是要产生$2^6$个分支，算下来如果不用这64个条件分支，而用大一统的方程应该是关于$x,y$的$4^{2^6}=340282366920938463463374607431768211456$次多项式方程

creasson

感觉目前几种代数计算方案，通过设$PA=s,PB=t,PC=p,PD=q$, 利用重心坐标给出内心表示式后化简所得的四内心共圆条件相对简化些。
为此整理出来，看将来是否能解决此问题，或以此证明某些特例情形。
令$Z = \frac{1 - uv}{1 + uv} + \frac{u + v}{1 + uv}i$,  $A = Z\left( a,b \right),B = Z\left( b, - 1 \right),C = Z\left( c, - 1 \right),D = Z \left( c,a \right)$ 是单位圆的外切四边形，且BC平行于$X$轴
其中参数$a > 0,b <-\frac{1}{a} < c < 1$用以保证四边形是逆时针方向的。
又令$P = x + yi$, 距离$s, t, p, q$ 满足等式：
$$1 + a^2 + b^2 + a^2 b^2 - s^2 - 2 a b s^2 - a^2 b^2 s^2 - 2 x +
2 a^2 b^2 x + x^2 + 2 a b x^2 + a^2 b^2 x^2 - 2 a y - 2 b y -
2 a^2 b y - 2 a b^2 y + y^2 + 2 a b y^2 + a^2 b^2 y^2=0 $$
$$ 2 + 2 b^2 - t^2 + 2 b t^2 - b^2 t^2 - 2 x + 2 b^2 x + x^2 - 2 b x^2 +
b^2 x^2 + 2 y - 4 b y + 2 b^2 y + y^2 - 2 b y^2 + b^2 y^2 = 0 $$
$$ 2 + 2 c^2 - p^2 + 2 c p^2 - c^2 p^2 - 2 x + 2 c^2 x + x^2 - 2 c x^2 +
c^2 x^2 + 2 y - 4 c y + 2 c^2 y + y^2 - 2 c y^2 + c^2 y^2 =0 $$
$$ 1 + a^2 + c^2 + a^2 c^2 - q^2 - 2 a c q^2 - a^2 c^2 q^2 -
2 x + 2 a^2 c^2 x + x^2 + 2 a c x^2 + a^2 c^2 x^2 - 2 a y - 2 c y -
2 a^2 c y - 2 a c^2 y + y^2 + 2 a c y^2 + a^2 c^2 y^2 = 0$$
四内心共圆的表达式可化简为关于$s,t,p,q$的一次式（其中$f_k$为关于$a,b,c,x,y$的多项式）：
\[ {f_1}stpq + {f_2}stp + {f_3}tpq + {f_4}pqs + {f_5}qst + .... + {f_{12}}s + {f_{13}}t + {f_{14}}p + {f_{15}}q + {f_{16}} = 0 \]
链接: https://pan.baidu.com/s/1yPRjv9PRglswQMDZTWb9VQ 提取码: 2ai1

$\angleAPB+\angleCPD=2\angleAEB$的化简式为：
链接: https://pan.baidu.com/s/1cb9kaqIxnlACtPpSfR0_Vg 提取码: 871j

容易验证当$P$为对角线中垂线的交点时是成立的($p=s,q=t$)

creasson

取$a -> 2, b -> -5, c -> 1/3$时，解图为