四连通与八连通的较量

KeyTo9_Fans

之前我们提到了楼主的问题等价于

————————————
求$p$，使得$f(p,E)=0.5$。
————————————

这是因为我们定义的$f(p,S)$的含义是

—————————————
四连通绿方的落子概率为$p$，

双方从局面$S$开始对弈，

均采用最佳策略的时候，

四连通绿方的胜利概率。
—————————————

这个含义是通过定理$1$得到的。

当$S$是空棋盘$E$的时候，如何求$f(p,E)$的值呢？

为了能清楚地回答这个问题，我们先做两道简单的习题。

习题$1$：

$S=$(红红绿,白绿绿,绿红红)，求$f(p,S)$。

解：



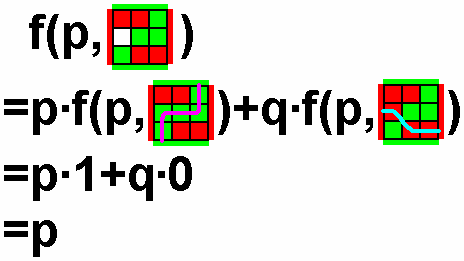习题$2$：

$S=$(红红绿,白绿绿,红绿红)，求$f(p,S)$。

解：



以上两道习题都很简单。

因为局面$S$只有$1$个空格子，

所以我们把这个空格子分两种情况讨论：

$1$.这个空格子被四连通绿方占据，概率为$p$；

$2$.这个空格子被八连通红方占据，概率为$q$。

然后把这两种情况综合起来就得到了结果。

如果局面$S$有$2$个空格子，就没有这么简单了。

因为双方都面临$2$个选择。

对于四连通绿方来说，他要比较$f(p,P_1)$和$f(p,P_2)$哪个大。

如果$f(p,P_1)$大，那么他就把$S$变成$P_1$；

如果$f(p,P_2)$大，那么他就把$S$变成$P_2$。

而$f(p,P_1)$和$f(p,P_2)$都是只有$1$个空格子的简单问题，所以可直接求得答案。

对于八连通红方来说，他要比较$f(p,Q_1)$和$f(p,Q_2)$哪个小。

如果$f(p,Q_1)$小，那么他就把$S$变成$Q_1$；

如果$f(p,Q_2)$小，那么他就把$S$变成$Q_2$。

而$f(p,Q_1)$和$f(p,Q_2)$也都是只有$1$个空格子的简单问题，所以也直接求得答案。

通过上述分析，我们就可以清楚地认识到：

对于没有空格子的终局$F$，$f(p,F)$是已知量。

对于有$1$个空格子的局面$S$，可根据相应的$f(p,F)$求得$f(p,S)$。

解决了$1$个空格子的局面$S$的问题，就可以求$2$个空格子局面的$f(p,S)$。

……

解决了$m$个空格子的局面$S$的问题，就可以求$(m+1)$个空格子局面的$f(p,S)$。

下图形象地表示了这一过程。



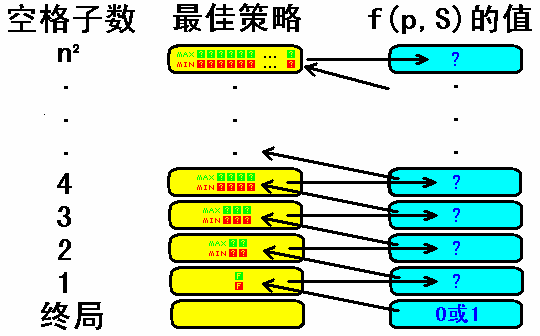好了，现在我们已经知道了：

$E$是空格子数最多的局面，有$N^2$个空格子。

（我们用$k$来表示局面$S$的空格子数）

要求$f(p,E)$，就要从$k=0$开始，求$k=1$的$f(p,S)$，$k=2$的，$k=3$的，……，$k=N^2-1$的。

最后才能根据$k=N^2-1$的$f(p,S)$求得$f(p,E)$的值。

我们重新翻出图$G(2)$来具体观察这一过程。



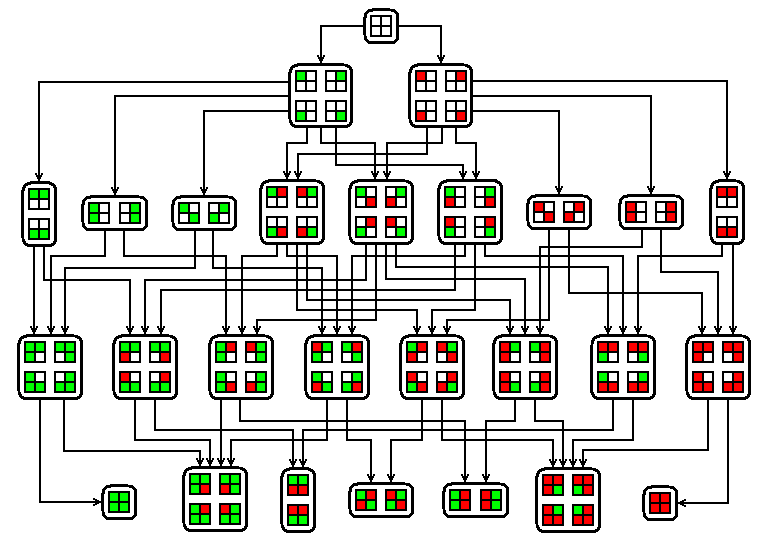图$G(2)$分了$5$层，其中最底层是$16$个终局$F$：



这一层的$f(p,S)$值不是$0$，就是$1$。

倒数$2$层是$k=1$的局面。



这一层的$f(p,S)$值由最底层的$f(p,S)$决定。

中间层是$k=2$的局面。



这一层的$f(p,S)$值由倒数$2$层的$f(p,S)$决定。

第$2$层是$k=3$的局面。



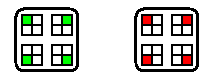这一层的$f(p,S)$值由第$3$层的$f(p,S)$决定。

最高层是空局面$E$。



只有当底下所有的$f(p,S)$求出来，才能求得$f(p,E)$。

通过上述分析，我们可以知道：

求$f(p,E)$就相当于在图$G$上遍历一遍，走遍所有的顶点和所有的边。

而图$G(N)$的顶点数为$3^{N*N}$，边数为$2/3*N^2*3^{N^2}$。

所以求$f(p,E)$的时间复杂度是$O(N^2*3^{N^2})$。

这个数列增长得很快。

前$5$项是：

$3$
$324$
$177147$
$688747536$
$21182215236075$

对于第$5$项，计算机已经无能为力了。

因为是实数运算，所以计算机每秒大约处理$10^8$次运算。

$21182215236075$次运算需要$211822$秒，约等于$3$天。

而令$f(p,E)=0.5$是一个二分（或者是迭代）的过程。

我们要对$p$进行猜测，然后看$f(p,E)$的值与$0.5$的差距，根据差距决定下一个$p$值。

而每算一次$f(p,E)$就要$3$天，这是不能接受的。

所以我们只能提供$N=1$到$N=4$的答案：

$N=1$: $p=0.50000000000000$
$N=2$: $p=0.54119610014620$
$N=3$: $p=0.55929631600132$
$N=4$: $p=0.56972413396803$

稍后讨论最佳策略下的博弈图（简称博弈图）。

KeyTo9_Fans

定义$4$：

—————————————————
对于给定的$p$，定义有向图$GB(p,N)$。

其顶点$S$是双方均采取最佳策略时对弈可达的局面。

对于每个顶点$S$（终局除外），都只有两条出边：

$S->P$，$S->Q$。

其中：

$S->P$是四连通绿方从局面$S$开始的最佳走法；

$S->Q$是八连通红方从局面$S$开始的最佳走法。

如果有多种最佳走法，则规定：

先从上到下，然后从左到右数，

数到第一个最佳的格子作为最佳的走法。
—————————————————

例如：

当$S=$(白白,白白)时，(绿白,白白)、(白绿,白白)、(白白,绿白)、(白白,白绿)都是四连通绿方的最佳走法。

根据先从上到下，然后从左到右数的规则，选取第一种走法(绿白,白白)为最佳走法。

下图是$GB(p,1)$。



下图是$GB(p,2)$（无论$p$取何值，双方的最佳走法不变）。



本贴的第一张图就是$GB(p,3)$（无论$p$取何值，双方的最佳走法不变）。



从上面的几幅图可以看出，$f(p,E)$是关于$p$的多项式函数。

$f(p,E)=0.5$是一个一元$N^2$次方程。

当$N>2$时，方程的次数大于$4$，没有公式解。

所以仍然需要用二分法（或迭代法）来求$p$。

要得到$f(p,E)$的多项式，我们需要预先知道最佳策略。

要知道最佳策略，就必须把$f(p,E)$底下的所有$f(p,S)$求出来。

时间复杂度仍然是$O(N^2*3^{N^2})$。

唯一的好处是我们可以很方便地得到更精确的结果：

$1$: $0.50000000000000000000000000000000$
$2$: $0.54119610014619698439972320536639$
$3$: $0.55929631600132353475576392078938$
$4$: $0.56972413396802715322804051835303$

楼主的问题解答到此告一段落。

稍后我将提出新的问题。

没——问题

终于连载完了，一直没好意思插楼，题解的连载比小说连载更吊胃口。。。
话说或许可以考虑下多项式的通项，而且目前对n->inf的情况也还没有讨论

KeyTo9_Fans

我一直都在很努力地画图。

因为没有图实在是太抽象，一点都不好解释。

花了很多时间，不好意思让你久等了。

你说得很正确。

我提出新问题的目的就是希望大家能参与进来一起讨论，

从而得到多项式的通项，最终得到n->inf的结果。

我在考虑新问题是直接在这里提还是开新贴。

我会尽快作决定的。

KeyTo9_Fans

新问题已经提出。点击此连接查看：

http://bbs.emath.ac.cn/thread-2710-1-1.html

欢迎讨论。

期限大概$1$个月。

如果没有收到满意的回复，Fans将再次出马，亲自上阵，继续连载，破解该题。

zgg___

LZ的这个问题连载中或许存在某个小缺陷，呵呵。
LZ说f(p,E)是关于p的多项式函数，或许还暗示了决策与p是无关的。

然而，在一些情况下，下一步的决策是与p相关的。
举一个例子来说，见下图的S，（我不知道是如何走到这种局面的。）
假设此时，四连通的绿方幸运的轮到了，那么他是选择1的位置还是选择2的位置呢？
设他选择1和2之后，获胜的几率分别是P1和P2，P1和P2的曲线如图，它们相交于0.618。因此，对于图中的S，f(p,S)是分段的多项式函数。在某些情况下，决策是和p相关的。这种可能性使得题目的复杂度有所增加。

或许游戏可以设计成这样：
1、每次投币，p=0.5；
2、棋盘变成长方形，让四连通的绿方的边比较长，从而补偿连通上的劣势。
问：棋盘的长宽是多少比较公平？

最后，支持7层的观点一下。（呵呵，只是感觉上的，联想起了围棋中扳粘和小尖的关系。）

KeyTo9_Fans

值得一提的是，连载中只有$1$个定理：$f(p,S)$是胜利概率。

除此之外，任何缺少严谨证明的论断，我都没有把它当成定理。（包括“必有一方获胜”和“不能同时获胜”）。

为了推翻“决策与$p$无关”的论断，我费尽心思去找反例。

结果找了很久，只找到$N=5$的一个反例。

由于过久没有关注这个问题，导致这个反例已经遗忘了。

根据即兴的回忆，这个反例大概是：

$S=$(白白白白白,绿绿绿白白,白白白白白,白白白白白,白白白红白)。

我在这里要赞一下楼上这位仁兄。

因为楼上找的这个反例比我找到的这个反例更有代表性。

其优点在于：

$1$. 简单。是$N=4$的反例。
$2$. 优美。以$0.618$作为分界点。

#####

另外，楼上提的新问题可以作为该问题的后续工作。

如果有必要，可以发起一个新话题。

我在这里还要出续集。

等续集完了之后会考虑楼上的新问题的。

KeyTo9_Fans

下集预告：

Fans的续集指的是什么呢？

他为什么扔下n->inf不管，就提出新问题了呢？

原来这个世界上不存在绝顶聪明的人。

即使存在，他们也太辛苦了。

他们的脑子要转$N^2*3^{N^2}$圈才能下一步棋，实在是太辛苦他们了。

如果能证明一个定理：

————————————————————————
两个问题的答案是相同的。

即对于所有的$N$，两个问题具有相同的公平概率$p$。
————————————————————————

我们就可以认为：

————————————————————————
两个绝顶聪明的人（比如emath和mathe）玩这个游戏，

等价于两个大笨蛋（比如Fans和东方角落）玩这个游戏。
————————————————————————

于是我们就不再需要当绝顶聪明的人了。

我们就可以轻轻松松地，以两个大笨蛋的角色去尽情享受这个游戏。

难怪Fans要提出新问题，让KeyTo9_Fans和KeyTo9都变成大笨蛋。

然而，zgg___仁兄指出：决策是与$p$值相关的。

这是否意味着绝顶聪明的人玩出来的多项式需要分段，大笨蛋玩出来的多项式不需要分段呢？

如果是的话，这无疑是上述定理的一个路障。

面对这个路障，Fans又是如何应对的呢？

他能顺利跨过这道坎吗？

敬请收看下集：《跨越路障》

KeyTo9_Fans

题解连续剧《跨越路障》现在开始！

定义$5$：

———————————————————
对于任意的局面$S$，定义函数$g(p,S)$。

$g(p,S)$的含义如下：

$p$是硬币抛到正面朝上的概率，

$k$是局面$S$的空白格数量，

我们连抛$k$次硬币，

然后根据抛硬币的结果依次给$k$个空白格涂上颜色：抛到正面涂绿色，抛到反面涂红色。

我们把涂完颜色后四连通绿方的胜利概率记为$g(p,S)$。
———————————————————

为了加深理解，我们来做一道习题。

习题$3$：$p=0.5$，$S=$(绿白,白白)，求$g(p,S)$的值。

答案将在下一次公布。

下一次讨论$g(p,S)$的显式表达式。

KeyTo9_Fans

下面公布习题$3$的答案。

————————————————————————
解：

因为$S=$(绿白,白白)，有$3$个空白格，

所以$k=3$，我们要连抛$3$次硬币。

连抛$3$次硬币有$2^3=8$种结果，对应$8$种涂色方案。

它们是：



因为$p=0.5$，所以每种涂色方案的概率均为$1/8$。

因为这$8$种涂色方案中，有$5$种涂色方案为四连通绿方胜利，

所以$g(p,S)=5/8$。
————————————————————————

定理$2$：

———————————————————
$g(p,S)=\sum_{i=0}^k c_i*p^i*q^{k-i}$

其中：

$q=1-p$，

$k$是局面$S$的空白格数量，

$c_i$是$i$个空白格涂绿色，$(k-i)$个空白格涂红色时，使得四连通绿方胜利的涂色方案数。
———————————————————

证明：

因为硬币抛到正面朝上的概率是$p$，反面朝上的概率是$q$，

所以出现包含$i$次正面朝上，$(k-i)$次反面朝上的特定的硬币序列的概率是$p^i*q^{k-i}$。

因为抛出两个不同的特定的硬币序列是两个不相容的事件，

所以根据$g(p,S)$的定义，

我们把使得四连通绿方胜利的特定的硬币序列的概率相加，

得到$g(p,S)=\sum_{i=0}^k c_i*p^i*q^{k-i}$。

证毕。

下一次讨论$g(p,S)$的递推式。