- 注册时间
- 2021-11-19
- 最后登录
- 1970-1-1
- 威望
- 星
- 金币
- 枚
- 贡献
- 分
- 经验
- 点
- 鲜花
- 朵
- 魅力
- 点
- 上传
- 次
- 下载
- 次
- 积分
- 9965
- 在线时间
- 小时
|
 发表于 2023-8-31 10:13:29
|
显示全部楼层
发表于 2023-8-31 10:13:29
|
显示全部楼层
本帖最后由 nyy 于 2023-8-31 10:20 编辑
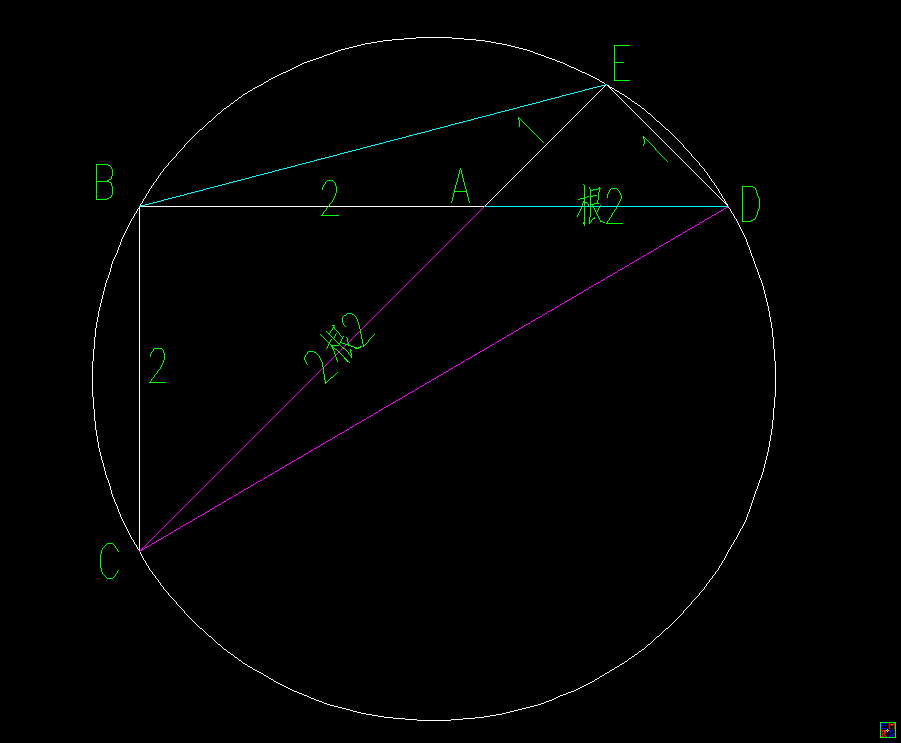
引用借用40楼的图。
利用40楼与41楼的两个图,组合交叉一下,又得到一个办法!
(*由∠CBE+∠CDE=180°,得到∠ABE+∠ADC=180-90-45=45°列方程1*),得到方程
\[\cos ^{-1}\left(\frac{\text{BE}^2+3}{4 \text{BE}}\right)+\cos ^{-1}\left(\frac{\text{CD}^2-6}{2 \sqrt{2} \text{CD}}\right)-\frac{\pi }{4}=0\]
(*圆内接四边形面积(婆罗摩笈多公式)=四个小三角形面积的和,列方程2*),得到方程
\[\frac{1}{4} \left(\sqrt{-\text{BE}^4+2 \text{BE}^2 \left(\text{CD}^2+5\right)+16 \text{BE} \text{CD}-\text{CD}^4+10 \text{CD}^2-9}-\sqrt{-\text{BE}^4+10 \text{BE}^2-9}-\sqrt{-\text{CD}^4+20 \text{CD}^2-36}-10\right)=0\]
先找出方程组的数值解!先画等值线图,交点就是方程组的解,图像如下:
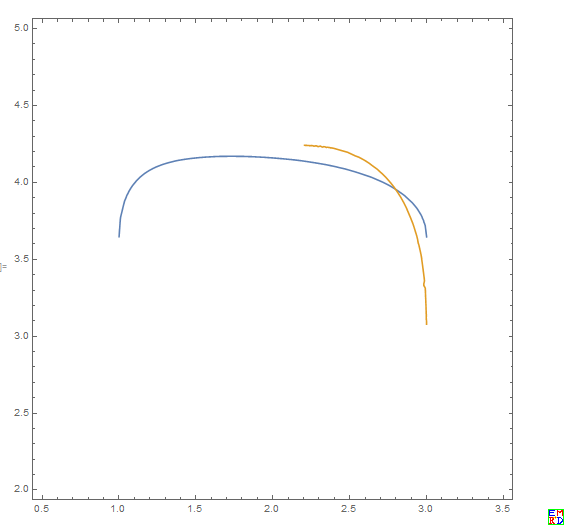
从图上可以看出方程组只有一个解,牛顿迭代法得到高精度数值解,得到
{BE -> 2.7979326519318134040630810788639975293470451277324777598618726\
46300747184075960598229656601002893606,
CD -> 3.9568743029684908345957334381028882136706148524629904443534491\
45402687924362251263097354440484226098}
由高精度数值解得到精确解,得到
\[\left\{\sqrt{2 \sqrt{2}+5},\sqrt{4 \sqrt{2}+10}\right\}\]
经过验根,这组根是方程组的解。
(*计算∠BAE、∠CAD的值(角度制)*)得到
{135, 135}
这两个角都是135°,容易知道CD是圆的直径。
代码如下:
- Clear["Global`*"];(*清除所有变量*)
- deg=Pi/180;(*角度制下1°所对应的弧度*)
- (*子函数,利用三边计算角的余弦值,角是c边所对的角*)
- cs[a_,b_,c_]:=((a^2+b^2-c^2)/(2*a*b))
- (*子函数,海伦公式,利用海伦公式计算三角形的面积*)
- heron[a_,b_,c_]:=Module[{p=(a+b+c)/2},Sqrt[p*(p-a)*(p-b)*(p-c)]]
- (*子函数,圆内接四边形面积公式(婆罗摩笈多公式)*)
- plmjd[a_,b_,c_,d_]:=Module[{p=(a+b+c+d)/2},Sqrt[(p-a)*(p-b)*(p-c)*(p-d)]]
- {AC,AD}={Sqrt[8],Sqrt[2]};(*已知长度的两条线段赋值*)
- (*由∠CBE+∠CDE=180°,得到∠ABE+∠ADC=180-90-45=45°列方程1*)
- eq1=ArcCos@cs[2,BE,1]+ArcCos@cs[AD,CD,AC]-45deg
- (*圆内接四边形面积(婆罗摩笈多公式)=四个小三角形面积的和,列方程2*)
- eq2=plmjd[2,CD,1,BE]-(heron[2,2,AC]+heron[AC,AD,CD]+heron[1,1,AD]+heron[2,1,BE])//Simplify
- (*绘制等值线图*)
- ContourPlot[{eq1==0,eq2==0},{BE,0.5,3.5},{CD,2,5},ImageSize->500]
- (*数值解找方程组的高精度数值解*)
- aaa=FindRoot[{eq1==0,eq2==0},{{BE,2},{CD,4}},WorkingPrecision->100,MaxIterations->200]
- (*由高精度数值解,得到精确解*)
- bbb=RootApproximant[{BE,CD}/.aaa]//ToRadicals//Simplify
- (*查看高精度数值解是否为方程组的解*)
- ccc={eq1==0,eq2==0}/.Thread[{BE,CD}->bbb]//FullSimplify
- (*计算∠BAE、∠CAD的值(角度制)*)
- ddd=ArcCos@{cs[2,1,BE],cs[AC,AD,CD]}/deg/.Thread[{BE,CD}->bbb]//FullSimplify
|
|